Ch3.2 Discrete Fourier Transform

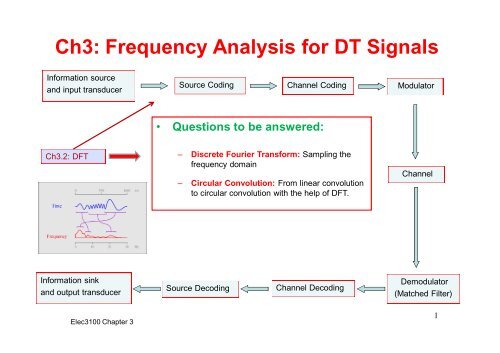
Ch3: Frequency Analysis for DT Signals 

Information source 

and input transducer 

Source Coding 

Channel Coding 

Modulator 

• Questions to be answered: 

Ch3.2: DFT 

– Discrete Fourier Transform: Sampling the 

frequency domain 

– Circular Convolution: From linear convolution 

to circular convolution with the help of DFT. 

Channel 

Information sink 

and output transducer 

Source Decoding 

Channel Decoding 

Demodulator 

(Matched Filter) 

Elec3100 Chapter 3 

1

Ch3.2: Discrete Fourier Transform 

• Discrete Fourier Transform 

• Circular Convolution 


2

WiFi and OFDM 


3

Discrete Time Fourier Transform (DTFT) 

• With DTFT, we have limited number of samples in time domain, 

but continuous function in the frequency domain. 

• As a result, DTFT is not directly applicable to the digital analysis. 

(Why?) 

• Questions: 

– Can we reconstruct the time-domain samples by part of the frequency 

domain signals? (Periodic?) 

– Can we utilize limited number of samples from the frequency-domain 

to reconstruct the time-domain samples? (Sampling Frequency- 

Domain?) 


4

Discrete Fourier Transform (DFT) 

• The simplest relation between a length-N sequence and its 

DTFT is obtained by uniformly sampling on the - 

axis at 

,01. 

 

• From the definition of DTFT, we have 

| 

 

 

 

 

 

• Note: is also a length-N sequence in the frequency domain. 


5

Inverse Discrete Fourier Transform (IDFT) 

• The sequence is called the discrete Fourier transform 

(DFT) of sequence . 

• Utilizing the notation , DFT is usually expressed as 

 

 

 

 

,01 

• The inverse discrete Fourier transform (IDFT) is given by 

 

1 

 

,01 

• Question: Can we uniquely reconstruct from ? In other words, 

is ? 


6

Inverse Discrete Fourier Transform (IDFT) 

• From the definition of the inverse discrete Fourier transform 

(IDFT), ∑ 

. 

 

• By substituting ∑ 

 

, we can obtain 

∑ 

∑ 

 

 

• Given ∑ 

 

 

we have . 

 

 

 

 

∑ ∑ 

 

 

∑ ∑ 

 

 

, for , an integer 

 

0, otherwise , 

• Thus, we can reconstruct from . 


7

Discrete Fourier Transform 

• Example: Consider the length-N sequence 

1, 0 

 

0, 1 1 

• Its N-point DFT is given by 

 

 

 

 

1,01 

0 

 

• Example: Consider the length-N sequence 

1, , 0 1 

 

0, otherwise 

• Its N-point DFT is given by 

∑ 

 

 

 

 

,0 1 


8

Discrete Fourier Transform 

• Example: Determine DFT of the length-N sequence 

cos 

,01 

 

• Using the trigonometric identity, we can obtain 

/ / = 

 

• The N-point DFT is given by 

∑ 

 

∑ 

 

 

∑ 

 

 

• Using the identity, ∑ 

 

 

we get 

 

 

 

 

,for 

,for 

0, otherwise 

, for , an integer 

 

0, otherwise 


9

• The DFT samples defined by 

Matrix Relations 

 

 

,0 1 

 

can be expressed in matrix form as where 

0 1 … 1 , 0 1 …1 

and 

is the DFT matrix given by 


10

Matrix Relations 

• The IDFT relation can be expressed as 

 

where is the IDFT matrix with ∗ where 


11

DFT Properties: Symmetry Relations 

Elec3100 Lecture 3 12

General Properties of DFT 


13

Physical Interpretation 

• Decomposition of a finite-length signal into a set 

of N sinusoidal components 

– Take an array of N complex sinusoidal generators; 

– Set the frequency of the k-th generator to 2/; 

– Set the amplitude of the k-th generator to , i.e. to the 

magnitude of the k-th DFT coefficient; 

– Set the phase of the k-th generator to ∡ , i.e. to the phase 

of the k-th DFT coefficient; 

– Start the generators at the same time and sum their outputs. 

• The first N output values of this “machine” are exactly x[n]. 


14

Physical Interpretation: Example 

cos 0, … , 63 

8 


15


cos 8 3 

0, … , 63 


16


cos 0, … , 63 

5 


17

Ch3.2: Frequency Analysis for DT Signals 

• Discrete Fourier Transform 

• Circular Convolution 


18

Circular Shift of a Sequence 

• Consider a length-N sequence defined for 01. 

Sample values are equal to zero for values of 0and . 

• For any arbitrary integer , the shifted sequence 

, is no longer defined for the range 0 1. 

• Thus, we need to define another type of “shift” that will always keep 

the shifted sequence in the range 0 1. 

• The desired shift, called the circular shift, is defined using a 

modulo operation: 

 

For 0(right circular shift), the above 

equation implies 

,for 1 

,for 0 


19

Circular Shift of a Sequence 

• A right circular shift by is equivalent to a left circular shift by 

sample periods. 

• A circular shift by an integer number greater than N is equivalent 

to a circular shift . 


20

Circular Convolution 

• Circular convolution is analogous to linear convolution, but with a 

subtle difference. 

• Consider two length-N sequences, and , respectively. 

• Their linear convolution results in a length 2 1 sequence 

given by 

 

,0 22 

 

• The longer form results from the time-reversal of the sequence 

and its linear shift to the right 


21


• To develop a convolution-like operation resulting in a length-N 

sequence , we need to define a circular time-reversal, and then 

apply a circular time-shift. 

• Resulting operation, called a circular convolution, is defined by 

∑ 

,01 

 

• Since the operation defined involves two length-N sequences, it is 

often referred to as an N-point circular convolution, denoted as 

N . 

• The circular convolution is commutative, 

 

N 

N 


22


• Example – Determine the 4-point circular convolution of two length- 

4 sequences: 1 2 0 1 and 2 2 1 1 as sketched 

below 

• The result is a length-4 sequence 

∑ 

N 

,03 

• For example, 

0 ∑ 

 

g0h0 g 1h3 g 2h2 g 3h1 

6 


23

Circular Convolution: DFT Method 

• Example – Determine the 4-point circular convolution of two length- 

4 sequences: 1 2 0 1 and 2 2 1 1 as sketched 

below 

• The 4-point DFT and are given by 

4, 1 , 2, 1 and 6, 1 , 0, 1 . 

• Thus, the 4-point DFT of is given by 

24, 2, 0, 2. 

• A 4-point IDFT of yields 

6 7 6 5 . 


24


• Example – Now let us extend the two length-4 sequences to 

length-7 by appending each with three zero-valued samples 

• We next determine the 7-point circular convolution and : 

∑ 

2, 6,5, 5, 4,1,1 

• It can be checked that is precisely the sequence 

obtained by a linear convolution of 


25



26



27



28



29

Linear Convolution Using the DFT 

• Linear convolution is a key operation in many signal processing 

applications. 

• Since a DFT can be efficiently implemented using FFT algorithms, 

it is of interest to develop methods for the implementation of linear 

convolution using the DFT. 

• Let and be two finite-length sequences of length N and M, 

respectively. Denote L=N+M-1. Define two length-L sequences 


30

Linear Convolution Using the DFT 


31

Ch3.2 Discrete Fourier Transform

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?