Ronnie Knikker, Villeurbanne, F - Eurotherm 2008

5th European Thermal-Sciences Conference, The Netherlands, 2008 

NUMERICAL STUDY OF BUOYANCY EFFECTS 

IN A CHANNEL FLOW GENERATED BY 

ASYMMETRIC WALL INJECTION 

R. Knikker, M. Michard, G. Bois 

CETHIL, CNRS, INSA-Lyon, Université Lyon1, F-69621, Villeurbanne, France. 

Abstract 

A numerical study is presented on the effects of buoyancy in a two-dimensional channel flow 

generated by wall injection in the unstably stratified regime for moderate Reynolds numbers. 

Fluid is injected with uniform velocity and temperature through a porous horizontal wall located 

in front of an impermeable wall at lower uniform temperature. The channel is closed on one 

side with an impermeable adiabatic wall. Buoyancy effects are characterised by the Richardson 

number. We show that for zero of low Richardson numbers, the flow is steady and presents 

a recirculation zone in the corner of the impermeable walls, growing in size with increasing 

buoyancy effects. Unsteady motion appears for Richardson numbers above a critical value, 

without external forcing of the flow. Initially, flow perturbations are periodic and remain 

confined to the region near the head end wall. At higher Richardson numbers, however, this 

unsteady motion triggers the intrinsic instability of this flow, called parietal vortex shedding. 

Resulting flow structures are amplified in the streamwise direction and affect in turn the thermal 

boundary layer further downstream. 

1 Introduction 

Natural and mixed convection have been extensively studied both for flows in closed cavities 

(Xin and Le Quéré, 2006) and for open channel flows (Nicolas, 2002), while the case of a semiopen 

channel flow generated by blowing through a porous wall with imposed temperature 

variations is less investigated regarding unsteady effects. The generic geometry of interest in 

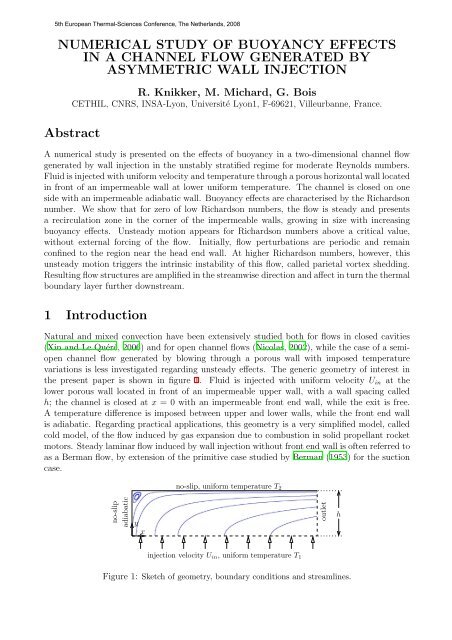
the present paper is shown in figure 1. Fluid is injected with uniform velocity U in at the 

lower porous wall located in front of an impermeable upper wall, with a wall spacing called 

h; the channel is closed at x = 0 with an impermeable front end wall, while the exit is free. 

A temperature difference is imposed between upper and lower walls, while the front end wall 

is adiabatic. Regarding practical applications, this geometry is a very simplified model, called 

cold model, of the flow induced by gas expansion due to combustion in solid propellant rocket 

motors. Steady laminar flow induced by wall injection without front end wall is often referred to 

as a Berman flow, by extension of the primitive case studied by Berman (1953) for the suction 

case. 

no-slip, uniform temperature T 2 

no-slip 

adiabatic 

y 

x 

outlet 

h 

injection velocity U in , uniform temperature T 1 

Figure 1: Sketch of geometry, boundary conditions and streamlines.


In the quasi-isothermal case, the control parameter is the injection Reynolds number Re in 

based on U in and h, and the main features of the flow are quite different from that observed 

in an open channel flow. First, due to uniform injection, the flow is accelerated and both bulk 

velocity U b and Reynolds number based on U b are increasing with the downstream distance 

x; therefore, some transition from a laminar state to a turbulent one is expected inside the 

channel and/or in boundary layers, even if acceleration is known to delay the transition. The 

second main feature of the flow induced by wall injection is that streamlines exhibit a strong 

curvature, due to the finite spacing between porous and impermeable walls. As a consequence, 

the flow exhibit some intrinsic instability, called parietal vortex shedding (PVS). 

For numerical simulation of the velocity field, the front end wall is generally removed in 

order to simplify the computations: the flow is supposed to be symmetric around the x = 0 

line, and the axial gradients of pressure and vertical velocity are set to zero. In such a case, for 

steady, laminar, incompressible flow, the velocity field show a self-similar solution well known 

in the literature. 

PVS has been predicted theoretically (Casalis et al., 1998) using stability analysis. The 

appearance of unsteady motion due to transition and PVS has also been numerically predicted, 

using statistical turbulence models (Kourta, 2004) or Large Eddy Simulations (Apte and Yang, 

2003; Chaouat and Schiestel, 2005); in some of these computations, a random forcing is introduced 

at the injection wall, either to trigger PVS or to simulate fluctuations of the injection 

velocity. Some studies take into account the front wall with a no-slip condition; in that case, the 

formation of a secondary vortex in the corner near the porous wall is mentioned (Apte and Yang, 

2003), but this eddy is generally considered as a numerically induced unwanted vortex. 

The characteristics of the Berman flow with both fluid injection and temperature variations 

are much less documented in the literature. For uniform injection and laminar, incompressible 

flow without front end wall nor buoyancy, both velocity and temperature fields show self-similar 

solutions; Fournier et al. (2007) determined the main properties of the temperature self-similar 

solution and heat transfer coefficient as a function of Reynolds and Peclet numbers, both for 

symmetric and non-symmetric injection; in Fournier et al. (2005), mass and heat transfer have 

been numerically studied using statistical models. Ferro and Gnavi (2002) studied the influence 

of viscosity variations due to temperature on the stability of the Berman flow, both for suction 

and injection cases, but without buoyancy effects. For studies related to solid-propellant rocket 

motors applications, the injection velocity and corresponding Reynolds numbers are generally 

relatively high; as a consequence, due to the downstream acceleration of the flow, Mach numbers 

inside the channel are not small, and compressibility effects can induce some temperature 

variations. Nevertheless, theses effects appear as second order phenomena, and do not modify 

the basic features of the velocity field, compared to an isothermal case (Apte and Yang, 2003; 

Chaouat and Schiestel, 2005). Finally, some papers (Chu et al., 2003) are devoted to the study 

of a reacting case with high temperature variations due to injection of reactive products. 

The objective of the present study is to investigate the effect of buoyancy on the flow 

dynamics in the unstably stratified case, for moderate Reynolds numbers. More precisely, we 

are focused on the characterisation of the vortex in the upper left corner due to the end wall, 

the appearance of unsteady motion for increasing buoyancy effects and the coupling between 

this unsteady motion and the intrinsic instability of the Berman (or Taylor) flow. 

Section 2 give in more details the governing equations and control parameters, and an 

overview of the numerical methods. In section 3, we present the main features of the flow without 

and with buoyancy, in a range of governing parameters where the flow remain steady. We 

then show that unsteady motion can appear for larger Richardson numbers. Final conclusions 

are drawn in section 4.


2 Methodology 

The configuration retained in this study is the two-dimensional channel (figure 1) closed by an 

adiabatic impermeable wall at the head end. Fluid at the temperature T 1 is injected homogeneously 

through the lower wall and the upper impermeable wall is at constant temperature 

T 2 . As mentioned previously, we focus on the case of unstably stratified flow, therefore T 2 < T 1 

when gravity forces are pointing in the usual downward direction. 

Physical model and governing equations 

Radiative heat fluxes and the effect of variable properties are neglected. The fluid motion and 

buoyancy effects are modelled by the Boussinesq approximation. Space variables, time, pressure 

and velocity components are normalised using the channel height h, the injection velocity U in 

and the reference density ρ. Under these assumptions, the continuity, momentum and energy 

equations are 

∇ · ⃗u = 0 

∂⃗u 

∂t + ⃗u · ∇⃗u = −∇p + Re−1 ∇ 2 ⃗u + Ri Θ (1) 

∂Θ 

∂t + ⃗u · ∇⃗ Θ = Pe −1 ∇ 2 Θ 

where Θ = (T −T 2 )/(T 1 −T 2 ) is the non-dimensional temperature, Re = U in h/ν is the Reynolds 

number based on the injection velocity, channel height and fluid viscosity ν and Pe = Re Pr 

is the Péclet number. The control parameter for buoyancy effects is the Richardson number, 

defined as 

Ri = gβ(T 1 − T 2 )h 

U 2 in 

where g is the gravitational acceleration and β is the coefficient of volumetric thermal expansion. 

Note that the Richardson and Rayleigh numbers are related through Ra = Ri Re 2 Pr. In this 

study, the Reynolds number is fixed at Re = 200 and the Prandtl number is Pr = 0.7. 

Numerical method 

The governing equations (1) are solved on a staggered Cartesian non-uniform grid. Fourthorder 

compact discretization (Lele, 1992) is used for all spatial derivatives and the resulting 

ODE is advanced in time using the semi-implicit third-order Runge-Kutta/Crank-Nicolson 

scheme proposed by Spalart et al. (1991). Similar methods for incompressible flows are used 

by Brüger et al. (2005), Kampanis and Ekaterinaris (2006) and Vedy et al. (2003) and have 

shown to be accurate and efficient for unsteady incompressible flows. The pressure equation 

is discretized in a consistent way using fourth-order schemes and solved using an iterative 

technique. A second-order discrete Poisson operator is used at each iteration and solved using 

generalized cyclic reduction (Swarztrauber, 1974). A fourth-order accurate solution of the 

pressure is obtained after several iterations. 

Special attention has been payed to the discretization of the non-linear terms in equations 

(1). The advection term in the momentum equation is recast in the so-called skewsymmetric 

formulation and discretized using centered compact schemes. In this way, the 

method is stable and conserves correctly the total kinetic energy in the limit of isothermal 

inviscid flows (Schiestel and Viazzo, 1995). The same procedure applied to the advection term 

in the energy equation leads to unphysical oscillations. This term is therefore rewritten in divergence 

form and discretized using a third-order upwind interpolation of the temperature followed 

by centered compact finite differencing of the energy flux. Thermal energy is then correctly 

conserved and the method is stable due to upwinding. The diffusion terms are discretized using


centered schemes. Physical boundary conditions are implemented directly into the schemes 

whenever possible. Otherwise, third-order one-sided schemes are used for the boundary points. 

A constant pressure boundary condition is used to model the outflow conditions at the right 

boundary. 

The accuracy of the numerical method is verified using the self-similar solution for the 

Berman problem by replacing the head wall with an adiabatic slip boundary. A correct convergence 

of the numerical solution is obtained on the entire computational domain, except for 

the region near the outlet boundary which is affected by the constant pressure condition. To 

minimise the influence of the outlet boundary, all other computations are calculated on a computational 

domain of length 30 h. A non-uniform grid is used of size 768 ×64. The grid spacing 

in the x-direction varies smoothly from 0.011h near the wall to 0.064h at the outlet, and in 

the y-direction from 0.011h near the boundaries to 0.017h at the center of the channel. The 

inlet velocity near the head end wall is defined by a boundary layer profile to comply with the 

no-slip boundary condition at x = 0. This profile covers roughly 6 grid points near the wall and 

is found to have negligible influence on the remaining flow structures. All other computations 

are calculated with the no-slip boundary condition at the left wall. 

3 Results 

Steady flow topology 

For small values of the Richardson number and a Reynolds number of Re = 200 the flow is 

found to be steady. Figure 2 illustrates the temperature distribution and flow pattern in the 

range Ri = 0 to 18. In the absence of buoyancy effects (Ri = 0), a small recirculation zone is 

visible in the upper left corner. According to Moffatt (1964), the formation of secondary eddies 

is expected in the upper left corner where the flow is dominated by viscous effects. Moffat 

predicted that any flow near the corner must consist of a sequence of eddies of decreasing size 

and rapidly decreasing intensity. For walls forming a right angle, the relative size of the vortices 

falls off in geometric progression whose value is around 10, while their relative intensity decay 

in a geometric progression with a common ratio near 2000. Therefore, we expect to capture no 

more than one counter-clockwise vortex in the upper left corner. 

Figure 2: Effect of buoyancy on the temperature field and streamlines in steady flow conditions. The 

downstream region for x > 2 is not shown for clarity.


In the presence of buoyancy effects, cold fluid falls along the end wall towards the porous 

wall. On the other hand, injection of hot fluid at the porous wall induces an upward motion; 

consequently the cold fluid flowing along the side wall is deviated towards the streamwise 

direction, and then transported upwards and remains trapped inside a vortex. As a result, the 

size of the counter-clockwise natural recirculation increases with increasing buoyancy effects. 

Unsteady flow 

Unsteady motion is observed for increasing buoyancy effects. The transition from a steady 

to unsteady flow is defined by a critical Richardson number that lies between Ri = 18 and 

Ri = 20. In terms of the Rayleigh number, unsteady flow appears between 5.04 × 10 5 and 

5.6 × 10 5 . Snapshots of the temperature distribution for several unsteady cases are shown in 

figure 3. Pockets of fresh fluid appear at the upper wall giving rise to buoyancy plumes ejected 

from the upper wall. Nevertheless, buoyancy effects are not sufficient to prevent damping of 

these plumes and the formation of a thermal boundary layer further downstream. For Ri ≤ 90, 

the thermal boundary layer is of constant thickness far downstream and described by the selfsimilar 

steady solution of the Berman problem. On the other hand, for Ri = 120 this boundary 

layer remains unsteady due to its interaction with parietal vortex shedding. 

Ri = 30 

Ri = 50 

Ri = 70 

Ri = 90 

Ri = 120 

Figure 3: Snapshots of the temperature distribution for different values of the Richardson number in 

the unsteady flow regime. 

Parietal vortex shedding 

Figure 4 shows snapshots of the vorticity field at different values of the Richardson number 

on a larger part of the computational domain. For high Richardson numbers, organized flow 

structures are observed near the injection wall on the right side of the computational domain. 

Similar flow structures, characteristic of parietal vortex shedding, are observed in the isothermal 

case by Apte and Yang (2003) after introduction of random perturbations to the injection 

velocity. For Ri = 90, these flow structures remain weak and disappear further downstream.


For Ri = 120, buoyancy plumes are sufficiently strong to trigger the instability and parietal 

vortex shedding is amplified as shown in figure 4. Interestingly, since the temperature field 

converges downstream to a boundary layer, the role of buoyancy in the formation of parietal 

vortex shedding is limited to the onset of the instability. 

Ri = 70 

Ri = 90 

Ri = 120 

Figure 4: Snapshots of the vorticity fields for different values of the Richardson number. An aspect 

ratio of 3 : 1 is used to enhance the visibility of flow structures. 

The mean fluctuation of temperature and velocity are shown in figure 5. For Ri = 90, 

the unsteady flow motion is strongest in the region near the head end vortex but decreases 

rapidly further downstream. For Ri = 120, fluctuations of both velocity and temperature 

are distributed over a much larger domain. Downstream of the vortex region, large velocity 

fluctuations are observed near the injection wall which are directly related to the presence of 

parietal vortex shedding. The temperature and velocity fluctuations near the upper boundary 

are due to perturbations of the boundary layer and the large gradients of temperature and 

velocity at this location. 

(a) Ri = 90 

Ri = 120 

(b) Ri = 90 

Ri = 120 

Figure 5: Standard deviation of temperature (a) and velocity fluctuation (b) for Ri = 90 and Ri = 120. 

The image aspect ratio is 3 : 1.


Spectral analysis 

Frequency spectra for the heat flux averaged along the upper wall for Ri = 30 and 120 are 

shown in figure 6a. At the lower Richardson number, the strong fundamental peak in the 

spectrum and the well-defined harmonics indicate that flow structures are essentially periodic. 

The power spectrum at Ri = 120 is a broad-band spectrum, despite the regular pattern of 

coherent structures resulting from parietal vortex shedding. 

Figure 6b plots the fundamental frequency of the periodic signal as a function of the Richardson 

number in the range Ri = 20 to 90 for which the flow is essentially periodic. Similar spectra 

and the same fundamental frequencies are obtained from the shear force at the head end wall. 

The frequency at Ri = 20 is of the order of U in /h and increases with buoyancy force. A jump 

in the frequency is observed around Ri = 49. 

Power spectral density 

10 0 Dimensionless frequency 

10 −5 

10 −10 

Ri=30 

Ri=120 

Dimensionless frequency 

3 

2.5 

2 

1.5 

1 

0.5 

(a) 

10 −15 

0 2 4 6 8 10 

(b) 

0 

0 20 40 60 80 100 

Richardson number 

Figure 6: Spectral analysis of the heat flux averaged along the upper wall; (a) power spectra for 

Ri = 30 and Ri = 120, (b) frequency of the most energetic mode for Richardson numbers between 0 

and 90. The frequency is expressed in non-dimensional units using U in /h. 

4 Conclusions 

The following main conclusions can be drawn from this two-dimensional numerical study. For 

zero or weak buoyancy force, the flow is steady and presents a recirculation zone in the upper 

left corner. The size of this recirculation zone increases with increasing buoyancy effect. The 

flow motion becomes unsteady above a certain critical Richardson number. For values near 

the critical one, flow perturbations are periodic and confined to the region near the head end 

wall. The fundamental frequency depends on the strength of the buoyancy force. For larger 

values of the Richardson number, the unsteady motion triggers the natural instability (PVS) 

of this flow. To our knowledge, this work is the first demonstration in this flow configuration of 

unsteady effects resulting from buoyancy forces. Note that no artificial forcing is used in this 

study and boundary conditions are steady. 

However, it is well known that for channel flows of the Poiseuille-Rayleigh-Bénard type threedimensional 

effects in the form of longitudinal rolls appear with increasing thermal stratification 

(Xin et al., 2006). It remains to be explored under which conditions similar flow structures 

appear in the present accelerated channel flow, in particular with respect to the unsteady twodimensional 

flow structures observed in this study. Further research is also needed to understand 

the physical mechanisms underlying unsteadiness and determine the essential parameters of this 

flow as well as the cause of the frequency jump observed in the periodic flow regime.


References 

S. Xin and P. Le Quéré. Natural-convection flows in air-filled, differential heated cavities with adiabatic 

horizontal walls. Numerical Heat Transfer, Part A, 50:437–466, 2006. 

X. Nicolas. Bibliographical review on the Poiseuille-Rayleigh-Bénard flows: the mixed convection flows 

in horizontal rectangular ducts heated from below. International Journal of Thermal Sciences, 41: 

961–1016, 2002. 

A. Berman. Laminar flow in channels with porous wall. J. Appl. Phys., 24 (9):456–475, 1953. 

G. Casalis, G. Avalon, and J.-Ph. Pineau. Spatial instability of planar channel flow with fluid injection 

through porous walls. Phys. Fluids, 10(10):2558–2568, 1998. 

A. Kourta. Instability of channel flow with fluid injection and parietal vortex shedding. Computers 

& Fluids, 33(2):155–178, 2004. 

S. Apte and V. Yang. A large-eddy simulation study of transition and flow instability in a porouswalled 

chamber with mass injection. J. Fluid Mech., 477:215–225, 2003. 

B. Chaouat and R. Schiestel. A new partially integrated transport model for subgrig-scale stresses 

and dissipation rate for turbulent developing flows. Physics of Fluids, 17(6):065106, 2005. 

C. Fournier, M. Michard, and F. Bataille. Heat transfer in a laminar channel flow generated by 

injection through porous walls. Journal of Fluids Engineering, 129:1048–1057, 2007. 

C Fournier, F Bataille, and M Michard. Transition characteristics of flowfield in a non-isothermal 

duct with wall injection. In Proceedings of 4th International Conference on Computational Heat 

and Mass transfer, pages 899–904, Paris, France, 2005. 

S. Ferro and G. Gnavi. Effects of temperature-dependent viscosity in channels with porous walls. Phys 

Fluids, 14(2):839 – 849, 2002. 

W.-W. Chu, V. Yang, and J. Majdalani. Premixed flame response to acoustic waves in a porous-walled 

chamber with surface mass injection. Combustion and Flame, 133(3):359–370, May 2003. 

S.K. Lele. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys., 103(1): 

16–42, 1992. 

P.R. Spalart, R.D. Moser, and M.M. Rogers. Spectral methods for the Navier-Stokes equations with 

one infinite and two periodic directions. J. Comput. Phys., 96(2):297–324, 1991. 

A. Brüger, B. Gustafsson, P. Lotstedt, and J. Nilsson. High order accurate solution of the incompressible 

Navier-Stokes equations. J. Comput. Phys., 203(1):49–71, February 2005. 

N.A. Kampanis and J.A. Ekaterinaris. A staggered grid, high-order accurate method for the incompressible 

Navier-Stokes equations. J. Comput. Phys., 215(2):589–613, July 2006. 

E. Vedy, S. Viazzo, and R. Schiestel. A high-order finite difference method for incompressible fluid 

turbulence simulations. Int. J. Num. Meth. Fluids, 42(11):1155–1188, 2003. 

P.N. Swarztrauber. Direct method for the discrete solution of separable elliptic equations. J. Numer. 

Anal., SIAM, 11:1136–1150, 1974. 

R. Schiestel and S. Viazzo. A Hermitian-Fourier numerical method for solving the incompressible 

Navier-Stokes equations. Computers & Fluids, 24(6):739–752, 1995. 

H.K. Moffatt. Viscous and resistive eddies near a sharp corner. J. Fluid Mech., 18:1–18, 1964. 

S. Xin, X. Nicolas, and P. Le Quéré. Stability analyses of longitudinal rolls of Poiseuille-Rayleigh- 

Bénard flows in air-filled channels of finite transversal extension. Numerical Heat Transfer, Part A, 

50:467–490, 2006.

Ronnie Knikker, Villeurbanne, F - Eurotherm 2008

Create successful ePaper yourself

Delete template?

Save as template?