The Riemann Integral

36 1. The Riemann Integral
10
8
6
4
2
0
−2
−4
−2 −1 0 1 2 3
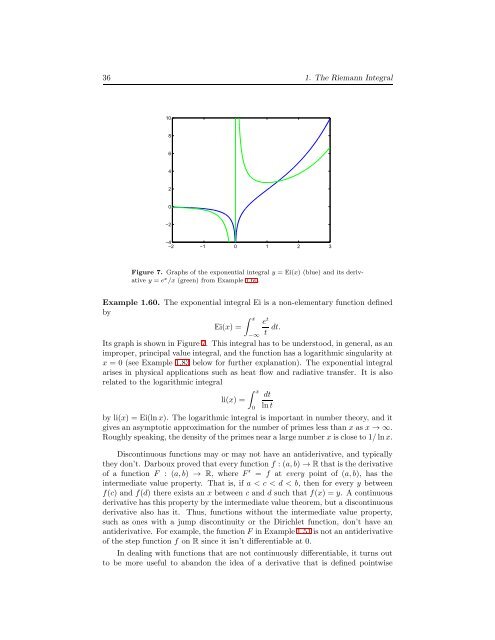
Figure 7. Graphs of the exponential integral y = Ei(x) (blue) and its derivative
y = e x /x (green) from Example 1.60.
Example 1.60. The exponential integral Ei is a non-elementary function defined
by
∫ x
e t
Ei(x) =
−∞ t dt.
Its graph is shown in Figure 7. This integral has to be understood, in general, as an
improper, principal value integral, and the function has a logarithmic singularity at
x = 0 (see Example 1.83 below for further explanation). The exponential integral
arises in physical applications such as heat flow and radiative transfer. It is also
related to the logarithmic integral
li(x) =
∫ x
by li(x) = Ei(lnx). The logarithmic integral is important in number theory, and it
gives an asymptotic approximation for the number of primes less than x as x → ∞.
Roughlyspeaking, thedensityofthe primesnearalargenumberxiscloseto1/lnx.
Discontinuous functions may or may not have an antiderivative, and typically
they don’t. Darboux provedthat everyfunction f : (a,b) → R that is the derivative
of a function F : (a,b) → R, where F ′ = f at every point of (a,b), has the
intermediate value property. That is, if a < c < d < b, then for every y between
f(c) and f(d) there exists an x between c and d such that f(x) = y. A continuous
derivative has this property by the intermediate value theorem, but a discontinuous
derivative also has it. Thus, functions without the intermediate value property,
such as ones with a jump discontinuity or the Dirichlet function, don’t have an
antiderivative. Forexample, the function F in Example1.51isnot anantiderivative
of the step function f on R since it isn’t differentiable at 0.
In dealing with functions that are not continuously differentiable, it turns out
to be more useful to abandon the idea of a derivative that is defined pointwise
0
dt
lnt