Normal Distribution Activity (solutions)

Normal Distribution Activity (solutions)
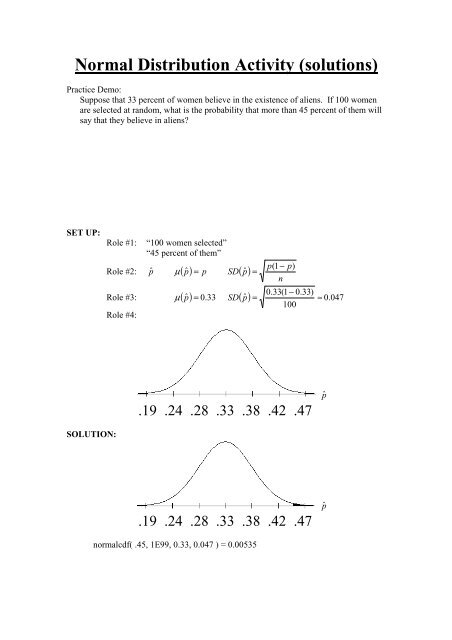
Practice Demo:
Suppose that 33 percent of women believe in the existence of aliens. If 100 women
are selected at random, what is the probability that more than 45 percent of them will
say that they believe in aliens?
SET UP:
Role #1:
“100 women selected”
“45 percent of them”
Role #2: pˆ µ ( p ˆ ) = p SD( pˆ
)
=
p(1
− p)
n
0.33(1 − 0.33)
SD ˆp
0.047
100
Role #3: µ ( pˆ ) = 0.33 ( ) =
≈
Role #4:
.19 .24 .28 .33 .38 .42 .47
pˆ
SOLUTION:
.19 .24 .28 .33 .38 .42 .47
pˆ
normalcdf( .45, 1E99, 0.33, 0.047 ) = 0.00535

Normal Distribution Activity (solutions)
1. Suppose family incomes in a town are normally distributed with a mean of $1,200
and a standard deviation of $600 per month. What is the probability that a family
has an income between $1,400 and $2,250?
SET UP:
Role #1: No sample of size greater than one was taken.
Family incomes are the population.
Role #2: X µ σ
Role #3: µ = 1200 σ = 600
Role #4:
-600 0 600 1200 1800 2400 3000
X
SOLUTION:
-600 0 600 1200 1800 2400 3000
X
normalcdf( 1400, 2250, 1200, 600 ) = 0.3294

Normal Distribution Activity (solutions)
2. An opinion poll asks, “Are you afraid to go outside at night within a mile of your
home because of crime?” Suppose that the proportion of all adults who would say
“Yes” to this question is 0.4. Assume that the poll obtained 20 answers randomly.
What percent of such polls with 20 responses have 10 or more say “Yes.”
SET UP:
Role #1:
“20 responses”
“10 or more say ‘Yes’”
“proportion of all adults”
Role #2: pˆ µ ( p ˆ ) = p SD( pˆ
)
=
p(1
− p)
n
0.4(1 − 0.4)
SD ˆp
0.110
20
Role #3: µ ( pˆ ) = 0.4 ( ) =
≈
Role #4:
.07 .18 .29 .4 .51 .62 .73
pˆ
SOLUTION:
Having 10 or more out of a sample of 20 say “Yes” is equivalent to having
10
p ˆ ≥ . In other words, p ˆ ≥ 0. 5 .
20
.07 .18 .29 .4 .51 .62 .73
pˆ
normalcdf( 0.5, 1E99, 0.4, 0.110 ) = 0.180655 or about 18.1% of such polls

Normal Distribution Activity (solutions)
3. Find the area under the curve between the z-scores of -2 and 1.
SET UP:
Role #1: No sample of size greater than one was taken.
“z-scores”
Role #2: z µ = 0 σ = 1
Role #3: µ = 0 σ = 1
Role #4:
-3 -2 -1 0 1 2 3
Z
SOLUTION:
-3 -2 -1 0 1 2 3
Z
normalcdf( -2, 1, 0, 1 ) = 0.81859

Normal Distribution Activity (solutions)
4. Adult nose length is normally distributed with mean 45mm and standard deviation
6mm. Find the probability that the sample mean nose length is between 44mm
and 46mm for random samples of 36 adults.
SET UP:
Role #1:
“samples of 36 adults”
“sample mean nose length”
Role #2: x µ ( x ) = µ SD( x)
Role #3: ( x) =
=
σ
n
SD x =
6
36
1
µ 45 ( ) =
Role #4:
42 43 44 45 46 47 48
x
SOLUTION:
42 43 44 45 46 47 48
x
By the Empirical Rule we see that the answer is about 68% because 44mm and
46mm is exactly one standard deviation each way on the sample mean nose
length distribution ( x distribution). More precisely we have
normalcdf( 44, 46, 45, 1 ) = 0.68269 or 68.269%

Normal Distribution Activity (solutions)
5. The weight of a particular brand of cookies has a normal distribution with a mean
weight of 32 ounces and a standard deviation of 0.3 ounces. When we look at the
mean weight of 20 packages, 68% of them will be between what two values?
SET UP:
Role #1:
“mean weight of 20 packages”
σ
=
n
0. 3
SD x = 0.067
20
Role #2: x µ ( x ) = µ SD( x)
Role #3: ( x) =
µ 32 ( ) ≈
Role #4:
SOLUTION:
31.80 31.87 31.93 32 32.07 32.13 32.20
x
x
31.80 31.87 31.93 32 32.07 32.13 32.20
Similar to the previous problem where we used the Empirical Rule, we see that
the answer is:
When we look at the mean weight of 20 packages ( x values) about 68%
of them will be between 31.93 ounces and 32.07 ounces.

Normal Distribution Activity (solutions)
6. A restaurateur anticipates serving about 180 people on a Friday evening, and
believes that about 20% of the patrons will order the chef’s steak special. How
many of those meals should he plan on serving in order to be pretty sure of having
enough steaks on hand to meet customer demand? Justify your answer, including
an explanation of what “pretty sure” means to you.
SET UP:
Role #1:
“serving about 180 people”
“20% of the patrons”
Role #2: pˆ µ ( p ˆ ) = p SD( pˆ
)
=
p(1
− p)
n
0.2(1 − 0.2)
SD ˆp
0.030
180
Role #3: µ ( pˆ ) = 0.2 ( ) =
≈
Role #4:
.11 .14 .17 .2 .23 .26 .29
pˆ
SOLUTION:
Here the population is all patrons that eat at that particular restaurant on Friday
nights. The 180 people on this Friday evening is a sample (although not SRS!).
The proportion of those 180 people ordering the chef’s steak special is the sample
proportion or pˆ value. What could this value be? According to the Empirical
Rule, we know that about 99.7% of all pˆ values occur between 0.11 and 0.29. It
is highly unlikely that pˆ is greater than 0.29 since this happens only about 0.15%
of the time ( 0 .3% = 0.15% ). Therefore, we would expect that the proportion of
2
the 180 patrons that order the chef’s steak would be no more than 0.29. Since
29% of 180 people is 52.2 people, we conclude that the restaurateur should plan
on serving 53 of those meals. That way the restaurateur can be “pretty sure” that
orders of chef’s steak on Friday evenings can be filled (about 99.7% of Friday
evenings).

Normal Distribution Activity (solutions)
7. In this example we will be interested in the heights of northern European males.
We take such a person and reduce him to a single number via the usual operations
for measuring someone's height. Then we model the height of northern European
males as a normal population with mu = 150 cm and sigma = 30 cm. If we
sample one northern European male, what's the probability that his height will fall
outside of 140 and 170? In other words, what are the chances that he'll be either
below 140, or he'll be above 170 in height? That's what we mean by the word
"outside."
SET UP:
Role #1: “sample one northern European”
Heights of northern European males are the population.
Role #2: X µ σ
Role #3: µ = 150 σ = 30
Role #4:
60 90 120 150 180 210 240
X
SOLUTION:
60 90 120 150 180 210 240
X
normalcdf( -1E99, 140, 150, 30 ) = 0.36944
normalcdf( 170, 1E99, 150, 30 ) = 0.25249
The probability that his height will fall outside 140 cm and 170 cm is
0.36944 + 0.25249 = 0.62193 or about 62.2% of the time.

Normal Distribution Activity (solutions)
8. Find the proportion of observations from the Standard Normal Distribution which
are below 2.45.
SET UP:
Role #1: No sample of size greater than one was taken.
“Standard Normal Distribution”
Role #1: z µ = 0 σ = 1
Role #2: µ = 0 σ = 1
Role #3:
-3 -2 -1 0 1 2 3
Z
SOLUTION:
-3 -2 -1 0 1 2 3
Z
The word “proportion” is this exercise can be misleading since it is referring to
the percentage (in decimal form) of z-scores less than 2.45. Here the proportion
value is equivalent to the shaded area of the curve.
normalcdf( -1E99, 2.45, 0, 1 ) = 0.99286