COLLISIONS IN ONE DIMENSION

7.7 Collisions in One Dimension 237
Example 7.8 Continued
have v y = 0 just after the explosion. Ignoring air resistance,
they land simultaneously. At that same instant, the center
of mass also reaches the ground.
Solution 1 First we make a sketch of the situation
(Fig. 7.15). At the top of the trajectory, where the explosion
occurs, v y = 0; the rocket is moving in the x-direction.
The initial momentum just before the explosion is entirely
in the x-direction. If M is the mass of the rocket, then
p ix = Mv ix
Just after the explosion, one-third of the mass of the rocket
is at rest; it then drops straight down under the influence of
the gravitational force. This piece has zero momentum just
after the explosion. To conserve momentum, the other twothirds
of the rocket must have a momentum equal to the
momentum just before the explosion.
p ix = p 1x + p 2x
Mv ix = 0 + ( 2 3 M)v 2x
Solving for v 2x , we find
v 2x = 3 2 v ix
The y-component of momentum must also be
conserved:
p iy = p 1y + p 2y
We know that both p iy and p 1y are zero; therefore, p 2y is
zero as well. Just after the explosion, both parts of the
rocket have zero vertical components of velocity. Then
both parts take the same time to fall to the ground as if the
rocket had not exploded. With a horizontal velocity larger
by a factor of 3 2 , the second piece of the rocket travels a
horizontal distance from the explosion a factor of 3 2 larger
than 260 m (see Fig. 7.15). The distance from the launch
point where this piece lands is
∆x = 260 m + 3 2 × 260 m = 650 m
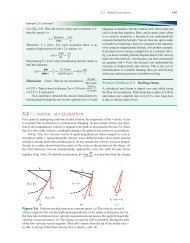
Figure 7.15
Rocket motion after explosion.
2 M
1
– M
3
v i
v iy
v ix
Solution 2 The piece with mass 1 3 M falls straight
down and lands 260 m from the launch point. After the
explosion, the CM continues to travel just as the rocket
itself would have done if it had not broken apart. From
the symmetry of the parabola, the CM touches the ground
at a distance of 2 × 260 m = 520 m from the launch point.
Since we know the location of the CM and that of one of
the pieces, we can find where the second piece lands:
Mx CM = 1 3 Mx 1 + 2 3 Mx 2
After canceling the common factor of M,
x CM = 1 3 x 1 + 2 3 x 2
Solving for x 2 yields
x 2 = 3x CM – x
1
= 3 × 520 m – 260 m
= 650 m
2
2
which is the same answer that we found in Solution 1.
Discussion The insight that the motion of the CM is
unaffected by internal interactions can be of enormous
help. Note, however, that Solution 2 would not be so simple
if the two fragments did not land simultaneously. As soon
as one fragment (fragment 1) hits the ground, the external
force on the system is no longer due exclusively to gravity,
so the CM doesn’t continue to follow the same parabolic
path. The normal and frictional forces acting on fragment 1
affect its subsequent motion and the subsequent motion of
the CM even though the motion of fragment 2 is unaffected.
Practice Problem 7.8
Revisited
Diana and the Raft
In Example 7.5, Diana (mass 55 kg) walks at 0.91 m/s
(relative to the water) on a raft of mass 100.0 kg. The raft
moves in the opposite direction at 0.50 m/s. Suppose it
takes her 3.0 s to walk from one end of the raft to the
other. (a) How far does Diana walk (relative to the
water)? (b) How far does the raft move
–
while Diana is walking? (c) How
3
far does the center of mass of
Diana and the raft move
during the 3.0 s?
0
M
260 m x
CM
7.7 COLLISIONS IN ONE DIMENSION
What is a collision? In the macroscopic world, a moving body bumps into another body
that may be at rest or in motion. The two bodies exert forces on each other while they
are in contact; as a result, their velocities change. In the microscopic and submicroscopic
world, our picture of a collision is different. When atoms collide, they don’t
“touch” each other: the atom doesn’t have a definite spatial boundary, so there are no

238 Chapter 7 Linear Momentum
Before
v = v i v = 0
v = 0 v = v i
(a)
After
v = v i
v = 0
Before
Figure 7.16 Two of the
many possible outcomes of a
collision between bumper
cars of equal mass with one
of them initially at rest.
(b)
After
1
v = – v
2 i
1
v = – v
2 i
surfaces to make “contact.” However, the collision model is still useful for atoms and
subatomic particles whenever there is an interaction in which the forces are strong
over a short time interval, so that there is a clear “before collision” and a clear “after
collision.”
We can often use conservation of momentum to analyze collisions even when
external forces act on the colliding objects. If the net external force is small compared to
the internal forces the colliding objects exert on one another during the collision, then
the change in the total momentum of the two objects is small compared to the transfer
of momentum from one object to the other. Then the total momentum after the collision
is approximately the same as it was before the collision.
The same techniques that are used for collisions in the macroscopic world (car
crashes, billiard ball collisions, baseball bats hitting balls) are also used in collisions in
the microscopic world (gas molecules colliding with each other and with surfaces,
radioactive decays of nuclei). First, we study collisions limited to motion along a line;
later, we consider collisions limited to motion in a plane (in two dimensions).
Suppose we observe a bumper car traveling at speed v i toward a second car that is
at rest. The masses of the two cars are equal. When the first car hits the second, what
happens?
Based on momentum considerations alone, there are many possible outcomes.
One possibility is that the first car stops moving and the second car moves off with
the same velocity that the first one had to begin with (Fig. 7.16a). This possibility
satisfies conservation of momentum because the total momentum is the same before
and after.
Another possibility is that the two cars stick together, moving away together
(Fig. 7.16b). With what speed do they move after the collision? If the momentum is
to be the same with twice as much mass moving, the speed must be half the initial
speed of the first car. There are many other possibilities. Conservation of momentum
doesn’t tell us which of these outcomes actually happens, but if we know one car’s
velocity after the collision, we can use momentum conservation to determine the
other car’s velocity.

7.7 Collisions in One Dimension 239
Example 7.9
Collision in the Air
Since m /m = 83.9/18.0 = 4.661, we can substitute m A krypton atom (mass 83.9 u) moving with a
p 1f p 2f ball moving along a track at 10.0 m/s. If the 2.0-kg ball is
velocity of 0.80 km/s to the right and a water molecule
(mass 18.0 u) moving with a velocity of 0.40 km/s
1 2 1
= 4.661m 2 :
4.661m 2 v 1f + m 2 v 2f = 4.661m 2 v 1i + m 2 v 2i
to the left collide head-on. The water molecule has a
The common factor m 2 cancels out. Solving for v 1f ,
velocity of 0.60 km/s to the right after the collision. What
is the velocity of the krypton atom after the collision? v 1f = 4.661v 1i
+ v 2i – v
2f
(The symbol “u” stands for the atomic mass unit.)
4.
661
4.661 × 0.80 km/s + (–0.40 km/s) – 0.60 km/s
Strategy Since we know both initial velocities and
=
4.661
one of the final velocities, we can find the second final = 0.59 km/s
velocity by applying momentum conservation. Let the
After the collision, the krypton atom moves to the right
subscript “1” refer to the krypton atom and let the subscript
“2” refer to the water molecule. Let the x-axis point
with a speed of 0.59 km/s.
to the right. Figure 7.17 shows before and after pictures
Discussion To check this result, we calculate the total
of the collision.
momentum (x-component) before and after the collision:
Solution Momentum conservation requires that the m 1 v 1i + m 2 v 2i = (83.9 u)(0.80 km/s) + (18.0 u)(–0.40 km/s)
final momentum be equal to the initial momentum:
= 60 u•km/s
p 1f + p 2f = p 1i + p 2i
m 1 v 1f + m 2 v 2f = (83.9 u)(0.59 km/s) + (18.0 u)(0.60 km/s)
= 60 u•km/s
Now we substitute p = mv for each momentum. It is easiest
to work in terms of components. For simplicity we
Momentum is conserved. There is no need to convert u to
kg since we only need to compare these two values.
drop the “x” subscripts, remembering that all quantities
If we made the mistake of thinking of momentum
refer to x-components:
as a scalar, we would get the wrong answer. The
m 1 v 1f + m 2 v 2f = m 1 v 1i + m 2 v 2i
sum of the magnitudes of the momenta before the collision
Before
is not equal to the sum of the magnitudes of the
momenta after the collision. Conservation of energy is
Kr
0.80 km/s 0.40 km/s
perhaps easier to understand intuitively since energy is a
H 2 O
scalar quantity. Converting kinetic energy to potential
energy is analogous to moving money from a checking
p 1i
p 2i
account to a savings account; the total amount of money
is the same before and after. This sort of analogy does not
After
work with momentum!
Kr
v 1f
0.60 km/s
H 2 O
Practice Problem 7.9 Head-On Collision
A 5.0-kg ball is at rest when it is struck head-on by a 2.0-kg
Figure 7.17
at rest after the collision, what is the speed of the 5.0-kg
Before and after snapshots of a collision.
ball after the collision?
Elastic and Inelastic Collisions
Collisions are often classified based on what happens to the kinetic energy of the colliding
objects. A ball dropped from a height h does not rebound to the same height. The
kinetic energy of the ball just after the collision with the floor or ground is less than it
was just before the collision; the amount of the kinetic energy decrease depends on the
makeup of the ball and the ground. A racquetball dropped onto a hard wooden floor
may rebound nearly to its original height, but a watermelon rebounds very little or not at
all. Why do some objects rebound much better than others?

240 Chapter 7 Linear Momentum
Imagine a racquetball colliding with the floor (Fig. 7.18). The bottom of the ball is
flattened. What makes the ball rebound from the floor? The forces holding the ball
together are like springs; the kinetic energy of the ball has been transformed largely into
potential energy stored in these springs. When the ball bounces back up, this energy is
transformed back into kinetic energy. Then why does the watermelon not rebound? The
watermelon, too, is deformed when it collides with the floor, but this deformation is not
reversible. The kinetic energy of the watermelon is changed mostly into thermal energy
rather than into potential energy.
A collision in which the total kinetic energy is the same before and after is called
elastic. When the final kinetic energy is less than the initial kinetic energy, the collision
is said to be inelastic. Collisions between macroscopic objects are generally inelastic to
some degree, but sometimes the change in kinetic energy is so small that we treat them
as elastic. When a collision results in two objects sticking together, the collision is perfectly
inelastic. The decrease of kinetic energy in a perfectly inelastic collision is as
large as possible (consistent with the conservation of momentum). Now that we have
defined elastic and inelastic collisions, we can put together a problem-solving strategy
for collision problems.
Problem-Solving Strategy for Collisions Involving Two Objects
1. Draw before and after diagrams of the collision.
2. Collect and organize information on the masses and velocities of the two objects
before and after the collision. Express the velocities in component form (with
correct algebraic signs).
3. Set the sum of the momenta of the two before the collision equal to the sum of
the momenta after the collision. Write one equation for each direction:
m 1 v 1ix + m 2 v 2ix = m 1 v 1fx + m 2 v 2fx
Figure 7.18 Deformation of a
racquetball during its collision
with the floor.
m 1 v 1iy + m 2 v 2iy = m 1 v 1fy + m 2 v 2fy
4. If the collision is known to be perfectly inelastic, set the final velocities equal:
v 1fx = v 2fx and v 1fy = v 2fy
5. If the collision is known to be perfectly elastic, then set the final kinetic energy
equal to the initial kinetic energy:
6. Solve for the unknown quantities.
1 2 m 1 v 2 1i + 1 2 m 2 v 2 2i = 1 2 m 1 v 2 1f + 1 2 m 2 v 2 2f
There is no conservation law for kinetic energy by itself. Total energy is always
conserved, but that does not preclude some kinetic energy being transformed into
another type of energy. The elastic collision is just a special kind of collision in which
no kinetic energy is changed into other forms of energy. Momentum is conserved
regardless of whether a collision is elastic or inelastic.
It can be proved (see Problem 56) that for any elastic collision between two
objects, the relative speed is the same before and after the collision. (This fact is most
useful in one-dimensional collisions; in two-dimensional collisions the direction of the
relative velocity changes due to the collision.) Since the relative velocity is in the opposite
direction after a one-dimensional collision—first the objects move together, then
they move apart—we can write:
v 2ix – v 1ix = –(v 2fx – v 1fx ) (7-14)
assuming the objects move along the x-axis. For a one-dimensional elastic collision,
Eq. (7-14) is a useful alternative to setting the final kinetic energy equal to the initial
kinetic energy.

7.7 Collisions in One Dimension 241
At a Route 3 highway on-ramp, a car of mass 1.50 × 10 3 kg
is stopped at a stop sign, waiting for a break in traffic
before merging with the cars on the highway. A pickup of
mass 2.00 × 10 3 kg comes up from behind and hits the
stopped car. Assuming the collision is elastic, how fast was
the pickup going just before the collision if the car is
pushed straight ahead onto the highway at 20.0 m/s just
after the collision?
Strategy Conservation of momentum will provide one
equation relating the initial and final velocities. That the
collision is elastic provides another equation. With two
unknown velocities, these two equations enable us to
solve for both. Let “1” refer to the car stopped at the stop
sign and “2” refer to the pickup. All motions are in one
direction, which we call the x-axis. To simplify the notation,
we drop the x subscripts and let all p’s and v’s refer
to x-components. Figure 7.19 shows a before and after
diagram for the collision.
Given: m 1 = 1.50 × 10 3 kg; m 2 = 2.00 × 10 3 kg; before the
collision, v 1i = 0; after the collision, v 1f = 20.0 m/s
To find: v 2i (speed of the pickup just before the collision)
Solution From conservation of momentum,
m 1 v 1i + m 2 v 2i = m 1 v 1f + m 2 v 2f (1)
where we cross out the first term because v 1i = 0. The collision
is elastic, so the relative velocity after the collision
Before
Example 7.10
Collision at the Highway Entry Ramp
v 2i
m 1
m 2
v 1i = 0
is equal and opposite to the relative velocity before the
collision [Eq. (7-14)]:
v 2i – v 1i = –(v 2f – v 1f ) (2)
We want to solve these two equations for v 2i , so we can
eliminate v 2f . Multiplying Eq. (2) through by m 2 and rearranging
yields
m 2 v 2i = m 2 v 1f – m 2 v 2f (3)
Adding Eqs. (1) and (3) gives
2m 2 v 2i = (m 1 + m 2 )v 1f (4)
Finally, we solve Eq. (4) for v 2i :
v 2i = m 1 + m
v 2
2m 1f = 1500 kg
+ 2000 kg
× 20.0 m/s = 17.5 m/s
2 4000
kg
Discussion To check this answer, first solve for v 2f .
Then you can verify that momentum is conserved [Eq. (1)]
and that the relative velocity changes sign [Eq. (2)]. You
can also calculate the total kinetic energy before and after
the collision and show they are equal, as they must be for an
elastic collision. We leave these checks to you for practice.
The road exerts frictional forces on the vehicles, so
the net external force on the vehicles was not zero during
the collision. We still use conservation of momentum
because during the short time interval of the collision,
friction doesn’t have time to change the system’s
momentum significantly.
Practice Problem 7.10 Perfectly Inelastic
Collision Between the Cars
Instead of colliding elastically, suppose the two vehicles
lock bumpers when they collide. With the same initial
conditions (v 1i = 0 and v 2i = 17.5 m/s),
find the speed at which the car would
x be pushed out onto the highway.
After
m 2
v 2f
m 1
v 1f = 20.0 m/s
Figure 7.19
Before and after diagrams of the collision
(side view).
Suppose in Example 7.10 that the entry ramp speed limit is 20 mi/h (8.94 m/s). By
measuring the length of the skid marks from the stop sign and estimating the coefficient
of friction, the accident investigator can determine that the car was pushed onto the
highway at a speed of 20.0 m/s. Witnesses confirm that the car was stopped before the
collision. Then the investigator calculates the speed of the pickup just before the collision
using conservation of momentum and, finding that it exceeds the speed limit, adds
speeding to the charges against the driver of the pickup.