Subtracting Vectors Components of a Vector

58 Chapter 3 Motion in a Plane
Example 3.1 Continued
Rounding to two significant figures, the total displacement
A + B + C has magnitude 45 km and is directed 30°
south of east.
Discussion Note that the answer includes both the
magnitude and direction of the displacement. If a
homework or exam question has you calculate a
vector quantity such as position or velocity, don’t
forget to specify the direction as well as the magnitude in
your answer. One without the other is incomplete.
Although the magnitude and direction of a position
vector depends on the choice of origin, the magnitude
and direction of a displacement (change of position) does
not depend on the choice of origin.
The total distance traveled by Charlotte and Shona is
18 km + 17 km + 48 km = 83 km, which is not equal to
the magnitude of the total displacement. Finding the total
distance involves adding three scalars, while finding the
total displacement involves adding three vectors. The
magnitude of the total displacement is the straight-line
distance from Killarney to Cork.
Practice Problem 3.1
A Traveling Executive
An executive flies from Kansas City to Chicago (displacement
= 400 mi in the direction 30° north of east) and
then from Chicago to Tulsa (600 mi, 45° south of west).
Add the two displacements graphically to find the total
displacement from Kansas City to Chicago.
Vector Subtraction:
A – B = A +(–B ), where –B has the
same magnitude as B but is opposite
in direction. Note that the order
matters: B – A = –(A – B ).
Subtracting Vectors
Displacement is defined as the difference between the initial and final position vectors:
∆ r = r f – r i (3-1)
Since the positions are vector quantities, the operation indicated in Eq. (3-1) is a vector
subtraction. To subtract a vector is to add its opposite (that is, a vector with the same
magnitude but opposite direction): r f – r i = r f + (–r i ). Multiplying a vector by the scalar
–1 reverses the vector’s direction while leaving its magnitude unchanged, so
–r i =–1× r i is a vector equal in magnitude and opposite in direction to r i . Figure 3.4
shows the graphical subtraction of two position vectors to illustrate the displacement for
a trip from Killarney to Kenmare. This same procedure is used to subtract any kind of
vector quantity (velocity, acceleration, etc.).
3.2 VECTOR ADDITION AND SUBTRACTION
USING COMPONENTS
The process of finding the
components of a vector is
called resolving the vector into
its components.
Components of a Vector
Any vector can be expressed as the sum of vectors parallel to the x-, y-, and (if needed)
z-axes. The x-, y-, and z-components of a vector indicate the magnitude and direction of
the three vectors along the axes. The sign of a component indicates the direction along
that axis. The x-, y-, and z-components of vector A are written with subscripts as follows:
A x , A y , and A z . One exception to this otherwise consistent notation is that the x-,
y-, and z-components of a position vector r are usually written simply x, y, and z
(instead of r x , r y , and r z ). For now we will deal only with vectors in the xy-plane.
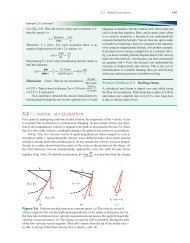
Figure 3.4 (a) Two position
vectors, r i and r f , drawn from an
arbitrary origin to the starting
point (Killarney) and to the ending
point (Cork) of a trip. (b) The
final position vector minus the initial
position vector is the displacement
∆r, found by adding –r i + r f .
Origin
Killarney
r i
(a)
r f
Cork
Killarney
–r i ∆r = –r i + r f
r f
Origin
(b)
Cork

3.2 Vector Addition and Subtraction Using Components 59
Components of vectors were introduced in Chapter 2, but only in cases where the
vectors were all parallel to a single axis. If a vector lies in the xy-plane but is not parallel
to either axis, then both its x- and y-components are nonzero.
Consider the velocity vector v in Fig. 3.5. We can think of v as the sum of two vectors,
one parallel to the x-axis and the other parallel to the y-axis. The magnitudes of
these two vectors are the magnitudes (absolute values) of the x- and y-components of v.
We can find the magnitudes of the components using the right triangle in Fig. 3.5 and the
trigonometric functions in Fig. 3.6. The length of the arrow represents the magnitude of
the vector (v = 9.4 m/s), so
adjacent
cos 58° = = v hy potenuse
v x opposite
and sin 58° = = v y
hy potenuse
v
Now we must determine the correct algebraic sign for each of the components.
From Fig. 3.5, the vector along the x-axis points in the positive x-direction and the vector
along the y-axis points in the negative y-direction, so in this case,
v x = +v cos 58° = 5.0 m/s and v y = –v sin 58° = –8.0 m/s
Using the right triangle in Fig. 3.7 gives the same values for the x- and y-components of
v since cos 32° = sin 58° and sin 32° = cos 58°.
y
58°
v x
v
v y
Figure 3.5 Resolving a
velocity vector v into x- and
y-components.
x
Problem-Solving Strategy: Finding the x- and y-Components of a Vector
from Its Magnitude and Direction
1. Draw a right triangle with the vector as the hypotenuse and the other two sides
parallel to the x- and y-axes.
2. Determine one of the unknown angles in the triangle.
3. Use trigonometric functions to find the magnitudes of the components. Make
sure your calculator is in “degree mode” to evaluate trigonometric functions of
angles in degrees and “radian mode” for angles in radians.
4. Determine the correct algebraic sign for each component.
We must also know how to reverse the process:
b
f
90°
Right triangle
c
q
a
f = 90° – q
Problem-Solving Strategy: Finding the Magnitude and Direction of a Vector
Afrom Its x- and y-Components
1. Sketch the vector on a set of x- and y-axes in the correct quadrant, according to
the signs of the components.
2. Draw a right triangle with the vector as the hypotenuse and the other two sides
parallel to the x- and y-axes.
3. In the right triangle, choose which of the unknown angles you want to determine.
4. Use the inverse tangent function to find the angle. The lengths of the sides of the triangle
represent A x and A y . If q is opposite the side parallel to the x-axis, then
tan q = opposite/adjacent = A x /A y . If q is opposite the side parallel to the y-axis,
then tan q = opposite/adjacent = A y /A x . If your calculator is in “degree mode,” then
the result of the inverse tangent operation will be in degrees. [In general, the inverse
tangent has two possible values between 0 and 360° because tan a = tan (a + 180°).
However, when the inverse tangent is used to find one of the angles in a right triangle,
the result can never be greater than 90°, so the value the calculator returns is the
one you want.]
5. Interpret the angle: specify whether it is the angle below the horizontal, or the
angle west of south, or the angle clockwise from the negative y-axis, etc.
6. Use the Pythagorean theorem to find the magnitude of the vector.
A = A 2 x + A
2 y
sin q = ______________
side opposite ∠q
= _ b
hypotenuse c
cos q = ______________
side adjacent ∠q
= _ a
hypotenuse c
tan q = ______________
side opposite ∠q
= _ b
side adjacent ∠q a
Figure 3.6 Trigonometric
functions (see Appendix A.7 for
more information).
y
32°
v y
v x
v
Figure 3.7 Resolving the
velocity vector into components
using a different right triangle.
x

60 Chapter 3 Motion in a Plane
Suppose we knew the components of the velocity vector in Fig. 3.5, but not the
magnitude and direction. Let us find the angle q between v and the +x-axis:
q = tan –1 o pposite
= tan –1 v y
= tan –1 8 . 0 m/
s
= 58°
adjacent
v
5.
0 m/
s
The magnitude of v is
v = v 2 2
x + v y = (+5.0 /s) m–8.0 2 + ( /s) m 2 = 9.4 m/s
x
Adding Vectors Using Components
It is generally easier and more accurate to add vectors algebraically rather than graphically.
The algebraic method relies on adding the components of the vectors. Remember
that each vector is thought of as the sum of vectors parallel to the axes (Fig. 3.8a). When
adding vectors, we can add them in any order and group them as we please. So we can
sum the x-components to find the x-component of the sum (Fig. 3.8b) and then do the
same with the y-components (Fig. 3.8c):
C = A + B if and only if C x = A x + B x and C y = A y + B y (3-2)
In Eq. (3-2), remember that A x + B x represents ordinary addition since the signs of the
components carry the direction information.
Problem-Solving Strategy: Adding Vectors Using Components
1. Find the x- and y-components of each vector to be added.
2. Add the x-components (with their algebraic signs) of the vectors to find the x-
component of the sum. (If the signs are not correct, the sum will not be correct.)
3. Add the y-components (with their algebraic signs) of the vectors to find the y-
component of the sum.
4. If necessary, use the x- and y-components of the sum to find the magnitude and
direction of the sum.
Even when using the component method to add vectors, the graphical method is an
important first step. A rough sketch of vector addition, even one made without carefully
measuring the lengths or the angles, has important benefits. Sketching the vectors makes it
much easier to get the signs of the components correct. The graphical addition also serves
as a check on the answer—it provides an estimate of the magnitude and direction of the
sum, which can be used to check the algebraic answer. Graphical addition gives you a
mental picture of what is going on and an intuitive feel for the algebraic calculations.
B x
(a) (c)
A x
B x
A x
Figure 3.8 (a) C = A + B,
shown graphically with the x-
and y-components of each vector
illustrated. (b) C x = A x + B x ;
(c) C y = A y + B y .
B
C x
y
B
A A y
C = A + B
C y
B y
C y
A y
C x
(b)

3.2 Vector Addition and Subtraction Using Components 61
Choosing x- and y-Axes
A problem can be made easier to solve with a good choice of axes. We can choose any
direction we want for the x- and y-axes, as long as they are perpendicular to each other.
Three common choices are
• x-axis horizontal and y-axis vertical, when the vectors all lie in a vertical plane;
• x-axis east and y-axis north, when the vectors all lie in a horizontal plane; and
• x-axis parallel to an inclined surface and y-axis perpendicular to it.
Example 3.2
An Irish Adventure (2)
In the trip of Example 3.1, Charlotte and Shona drive at a
compass heading of 27° west of south for 18 km to
Kenmare, then directly south for 17 km to Glengariff, then
at a compass heading of 13° north of east for 48 km to
Cork. Use the component method to find the magnitude
and direction of the displacement vector for the entire trip.
Strategy As before, let’s call the three successive displacements
A, B, and C, respectively. To add the vectors
using components, we first choose directions for the x-
and y-axes. Then we find the x- and y-components of the
three displacements. Adding the x- or y-components of
the three displacements gives the x- or y-component of the
total displacement. Finally, from the components we find
the magnitude and direction of the total displacement.
Solution A good choice is the conventional one: x-
axis to the east and the y-axis to the north. The first displacement
( A) is directed 27° west of south. Both of its
components are negative since west is the –x-direction
and south is the –y-direction. Using the triangle in
Fig. 3.9, the side of the triangle opposite the 27° angle is
parallel to the x-axis. The sine function relates the opposite
side to the hypotenuse:
A x = –A sin 27° = –18 km × 0.454 = –8.17 km
where A is the magnitude of A. The cosine relates the
adjacent side to the hypotenuse:
A y = –A cos 27° = –18 km × 0.891 = –16.0 km
Displacement B has no x-component since its direction
is south. Therefore,
B x = 0 and B y = –17 km
The direction of C is 13° north of east. Both its components
are positive. From Fig. 3.9, the side of the triangle
opposite the 13° angle is parallel to the y-axis, so
y
A = 18 km 27° B = 17 km C = 48 km
A A
C
y
B
13°
C y
x
A x
C x
Figure 3.9
Resolving A, B, and C into x- and y-components.
C x = +C cos 13° = +48 km × 0.974 = +46.8 km
C y = +C sin 13° = +48 km × 0.225 = +10.8 km
Now we sum the x- and y-components separately to
find the x- and y-components of the total displacement:
∆x = C x + B x + A x
= 46.8 km + 0 + (–8.17 km) = +38.63 km
∆y = C y + B y + A y
= 10.8 km + (–17 km) + (–16.0 km) = –22.2 km
The magnitude and direction of ∆r can be found from
the triangle in Fig. 3.10. The magnitude is represented by
the hypotenuse:
∆r = (∆x) 2 + (∆y) 2 = (38.63 km) 2 + (–22.2km) 2
= 45 km
The angle q is
q = tan –1 o pposite
= tan –1 22.
2 km
= 30°
adjacent
3 8.
63
km
Since +x is east and –y is
south, the direction of the
displacement is 30° south
of east. The magnitude
and direction of the displacement
found using
components agree with
the displacement found
graphically in Fig. 3.3.
Discussion Note that the x-component of one displacement
was found using the sine function while another was
found using the cosine. The x-component (or the y-
component) of the vector can be related to either the sine or
the cosine, depending on which angle in the triangle is used.
Practice Problem 3.2
Coordinate Axes
38.63 km
θ
22.2 km
Changing the
Find the x- and y-components of the displacements for
the three legs of the trip if the x-axis points south and the
y-axis points east.
y
∆r
Figure 3.10
Finding the magnitude and
direction of ∆r.
x