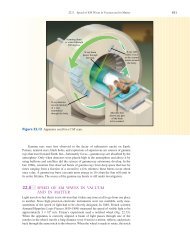
Subtracting Vectors Components of a Vector

3.2 Vector Addition and Subtraction Using Components 59
Components of vectors were introduced in Chapter 2, but only in cases where the
vectors were all parallel to a single axis. If a vector lies in the xy-plane but is not parallel
to either axis, then both its x- and y-components are nonzero.
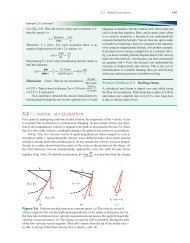
Consider the velocity vector v in Fig. 3.5. We can think of v as the sum of two vectors,
one parallel to the x-axis and the other parallel to the y-axis. The magnitudes of
these two vectors are the magnitudes (absolute values) of the x- and y-components of v.
We can find the magnitudes of the components using the right triangle in Fig. 3.5 and the
trigonometric functions in Fig. 3.6. The length of the arrow represents the magnitude of
the vector (v = 9.4 m/s), so
adjacent
cos 58° = = v hy potenuse
v x opposite
and sin 58° = = v y
hy potenuse
v
Now we must determine the correct algebraic sign for each of the components.
From Fig. 3.5, the vector along the x-axis points in the positive x-direction and the vector
along the y-axis points in the negative y-direction, so in this case,
v x = +v cos 58° = 5.0 m/s and v y = –v sin 58° = –8.0 m/s
Using the right triangle in Fig. 3.7 gives the same values for the x- and y-components of
v since cos 32° = sin 58° and sin 32° = cos 58°.
y
58°
v x
v
v y
Figure 3.5 Resolving a
velocity vector v into x- and
y-components.
x
Problem-Solving Strategy: Finding the x- and y-Components of a Vector
from Its Magnitude and Direction
1. Draw a right triangle with the vector as the hypotenuse and the other two sides
parallel to the x- and y-axes.
2. Determine one of the unknown angles in the triangle.
3. Use trigonometric functions to find the magnitudes of the components. Make
sure your calculator is in “degree mode” to evaluate trigonometric functions of
angles in degrees and “radian mode” for angles in radians.
4. Determine the correct algebraic sign for each component.
We must also know how to reverse the process:
b
f
90°
Right triangle
c
q
a
f = 90° – q
Problem-Solving Strategy: Finding the Magnitude and Direction of a Vector
Afrom Its x- and y-Components
1. Sketch the vector on a set of x- and y-axes in the correct quadrant, according to
the signs of the components.
2. Draw a right triangle with the vector as the hypotenuse and the other two sides
parallel to the x- and y-axes.
3. In the right triangle, choose which of the unknown angles you want to determine.
4. Use the inverse tangent function to find the angle. The lengths of the sides of the triangle
represent A x and A y . If q is opposite the side parallel to the x-axis, then
tan q = opposite/adjacent = A x /A y . If q is opposite the side parallel to the y-axis,
then tan q = opposite/adjacent = A y /A x . If your calculator is in “degree mode,” then
the result of the inverse tangent operation will be in degrees. [In general, the inverse
tangent has two possible values between 0 and 360° because tan a = tan (a + 180°).
However, when the inverse tangent is used to find one of the angles in a right triangle,
the result can never be greater than 90°, so the value the calculator returns is the
one you want.]
5. Interpret the angle: specify whether it is the angle below the horizontal, or the
angle west of south, or the angle clockwise from the negative y-axis, etc.
6. Use the Pythagorean theorem to find the magnitude of the vector.
A = A 2 x + A
2 y
sin q = ______________
side opposite ∠q
= _ b
hypotenuse c
cos q = ______________
side adjacent ∠q
= _ a
hypotenuse c
tan q = ______________
side opposite ∠q
= _ b
side adjacent ∠q a
Figure 3.6 Trigonometric
functions (see Appendix A.7 for
more information).
y
32°
v y
v x
v
Figure 3.7 Resolving the
velocity vector into components
using a different right triangle.
x