LECTURE 3: Polynomial interpolation and numerical differentiation

2 Polynomial interpolation
2.1 Interpolating polynomial
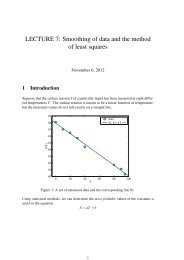
Given a set of n+1 data points {x i ,y i }, we want to find a polynomial curve that passes
through all the points. Thus, we look for a continuous curve which takes on the values y i
for each of the n+1 distinct x i ’s.
A polynomial p for which p(x i )=y i when 0≤i≤n is said to interpolate the given set of
data points. The points x i are called nodes.
The trivial case is n=0. Here a constant function p(x)=y 0 solves the problem.
The simplest case is n=1. In this case, the polynomial p is a straight line defined by
( ) ( )
x−x1 x−x0
p(x)= y 0 + y 1
x 0 − x 1 x 1 − x
( ) 0
y1 − y 0
= y 0 + (x−x 0 )
x 1 − x 0
Here p is used for linear interpolation.
As we will see, the interpolating polynomial can be written in a variety of forms, among
these are the Newton form and the Lagrange form. These forms are equivalent in the
sense that the polynomial in question is the one and the same (in fact, the solution to the
interpolation task is given by a unique polynomial)
We begin by discussing the conceptually simpler Lagrange form. However, a straightforward
implementation of this form is somewhat awkward to program and unsuitable for
numerical evaluation (e.g. the resulting algorithm gives no error estimate). The Newton
form is much more convenient and efficient, and therefore, it is used as the basis for
numerical algorithms.
2.2 Lagrange form
First define a system of n+1 special polynomials l i known as cardinal functions. These
have the following property:
{
0 if i≠ j
l i (x j )=δ i j =
1 if i= j
The cardinal functions l i can be written as the product of n linear functions (the variable
x occurs only in the numerator of each term; the denominators are just numbers):
( ) x−x j
l i (x)= (0≤i≤n)
x i − x j
=
n
∏
j≠i
j=0
( )( )
x−x0 x−x1
...
x i − x 0 x i − x 1
Thus l i is a polynomial of degree n.
( )( ) ( )
x−xi−1 x−xi+1 x−xn
...
x i − x i−1 x i − x i+1 x i − x n