12.010 HW 3 Solution 1 10/30/2000. 12.215 Homework #3 ... - MIT

12.010 HW 3 Solution 1 10/30/2000.
12.215 Homework #3 Solution Due Monday 10/30/2000
Latitude and Longitude determination.
(a) Find the time and the value of the maximum angle between the sun and its reflection
using the data given below (Note: Acroread has an option that allows text to be
copied from a PDF file, therefore it should not be necessary to re-type any of the
values). (10 points)
Sextant 10/00
75
74
2*Sun Elev (deg)
73
2*Sun Elev (deg)
73
72
72
72
71
Y = M0 + M1*x + ... M8*x 8 + M9*x 9
M0
-858.71
M1
113.17
M2
-3.4318
R
0.99882
70
15.4 15.6 15.8 16.0 16.2 16.4 16.6 16.8
GMT Hrs
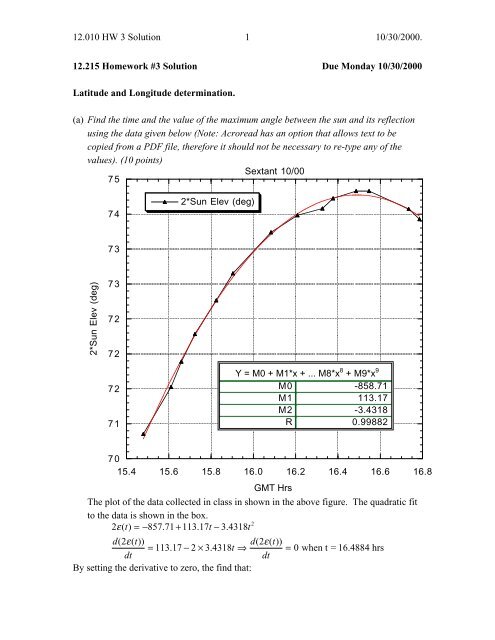
The plot of the data collected in class in shown in the above figure. The quadratic fit
to the data is shown in the box.
2
2ε( t) = − 857. 71 + 113. 17t − 3.
4318t
d( 2ε( t))
d( 2ε( t))
= 113. 17 − 2 × 3.
4318t
⇒ = 0 when t = 16.4884 hrs
dt
dt
By setting the derivative to zero, the find that:

12.010 HW 3 Solution 2 10/30/2000.
(a) Sun reached maximum elevation at 16.4884 hrs UT = 16 hrs 29 min 18 sec
(b) Find the mean index errors for the near and distance objects (5 points)
Mean index error for nearby objects is 11.0’
Mean index error of distant objects is 14.9’
(c) At the time of the maximum angle between the sun and its reflection, find the right
ascension (RA) and declination of the Sun, and the Greenwich Mean Sidereal Time
(GMST). You can use the nautical almanac in Lindgreen Library or the on-line
almanac referenced on the course web page. (10 points)
From the web site http://aa.usno.navy.mil/AA/data/docs/WebMICA_2.html that directly
allows calculations of the positions of astronomical positions we obtain for the
topocentric position of the Sun (these positions refer to a coordinate system whose origin
is at the surface of the Earth. An approximate position must be given for these positions).
2000 Oct 20 16:29:18.0 (UT1)
Object R.A. Dec. Dist. Z.D. Az. Elong. Diam. Mag
h m o ' A.U. o o o ' "
Sun 13 42.4 -10 37 0.995 51 181 ---- 32 08.0 ----
The other type of position is geocentric, apparent (meaning the value that would be seen)
coordinates and these are given below for the Sun. These values should differ at most by
the radius of the Earth divided by the distance to the sun (approximately 8.8”).
Date Time Right Declination Distance Equation
(UT1) Ascension of Time
h m s h m s o ' " AU m s
2000 Oct 20 16:29:18.0 13 42 25.924 - 10 36 46.37 0.995513510 +15 18.5
Greenwich Sidereal time has its own look up table and the value is.
Date Time Sidereal Time
h m s h m s
2000 Oct 20 16:29:18.0 18 27 03.5103
RA of Sun 13h 42m 25.92s 13.7072 hrs
Declination of Sun -10 o 36’ 46.37” -10.6129 deg
GST 18h 27m 03.51s 18.4510 hrs
(d) Using the mean index error for distance objects, compute the elevation angle to the
Sun at its maximum (5 points)

12.010 HW 3 Solution 3 10/30/2000.
Based on the quadratric fit in part (a), the maximum value of 2*elevation to Sun is
74.2879 degrees. Since when we knew the elevation angle was zero, the mean reading on
the Sextant was 14.9’ (0.2483 degree), the index error should be subtracted from the
above value and then divided by 2 to obtain the elevation angle.
Maximum elevation of Sun = 37.0198 deg.
(e) Compute the approximate atmospheric bending contribution to this measured
elevation to the sun (10 points)
The refraction correction is 1’/(tan ε + 0.03).
At 37.0198 deg., refraction correction is 1.3’ = 0.0213 deg which should be subtracted
from the apparent elevation.
(f) Given the declination of the Sun and the in vacuum estimate of the elevation angle to
the Sun, compute the latitude of the Green building. (10 points)
The figure below shows the geometry of the latitude determination
ε obs
∆ε Refraction
ε true
To Sun
φ
δ (negative)
To Sun
φ = [90 - ( ε obs -∆ε ) + δ]
The latitude, φ, is given by (90-ε c )-δ s = 42.3796 degrees = 42 o 22.8’ (Actual 42 o 21.6’)

12.010 HW 3 Solution 4 10/30/2000.
(g) Given the RA of the sun and the GST when the sun was at its maximum elevation
angle, compute the longitude of the Green building (10 points)
The longitude is RA s -GST = -4.7438 hrs = -71.157 deg = 71 o 9.4’ (Actual 71 o 4.8’)
(h) What would be the effect on the results from parts (f) and (g) if the near object index
error correction were used (10 points)
A change in the index error would effect the latitude (the effect is half the size since we
observed a reflection). There would be no effect on longitude.