Finding probabilities involving Z scores

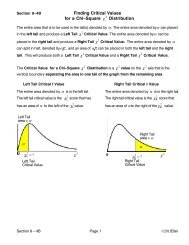
Example 5Finding the area to the left of a positive Z scoreP( z < 1.41 )If we want to find the probability of selecting one number from the z distribution and having thatnumber be less than the z value of 1.41 we need to find the area to the LEFT of z = 1.41The number at the intersection of the 1.4 row and the 0.01Positive Z Scorescolumn is 0.9207Standard Normal (Z) Distribution: Cumulative Area to the LEFT of ZZ 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.091.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319This means that the area to the left of z = 1.41 is 0.9207the area to the left ofz = 1.41 is .9207left tail area= .1539left tail area= .92070z =1.41positivevalueP( z < 1.41 ) = 0.9207Finding the area to the Right of a positive Z scoreP( z > 1.41 )If we want to find the probability of selecting one number from the z distribution and having thatnumber be more than the z value of 1.41 we need to find the area to the RIGHT of z = 1.41The total of the yellow and white areas is 1 so the right area (in white) = 1 – the left areaIf the area to the Left of Z = 1.41 is 0.9207then the area to the Right of Z = 1.41 is 1 – .9207 = .0793P( z > 1.41 ) = 1 –0.9207 = .0793Example 6Section 6 – 3B Lecture Page 10 of 16 © 2012 Eitel