Static analysis of cable structures 1. Introduction Cable structures ...

Static analysis of cable structures1. IntroductionCable structures are lightweight structures of flexible type. The typical cables structure is usuallycomposed of curved members. These members have only axial stiffness related to tension. Theycan carry neither bending nor compression. Some of them are load bearing ones, some aretightening.They allow spanning large distances. Therefore, they are used in the construction of large spanroof girders, shell-like roofs and hanging bridges.2. Types of cable structuresSingle cableqNNDouble cable girdersInitially tightened – they reach large stiffness. Hence, they exhibit smaller displacements thansingle cablesLoad-bearing cableTensile hangerTightening cableJahwert’s girderThere are also less frequently used double cable girders with compressive hangers.

Pylons may have various cross-sections– masts with guysMastGuy (cable)3. Basic equation for a single cableLet us consider a single cable subjected to the axial tightening force and transverse loading.NAqlR A =2flCqlR B =2qBNSince the cable carries no bending we can write down the equation of equilibrium of moments withrespect to the centre point C for a half of the cable∑ql l ql lNf − ⋅ + ⋅2 2 2 4M leftC =and get the basic relation between the tightening force and the uniform transverse loading2qlN = 8 f0

where the transformation matrix isKe= TTe~KeTeThe direction cosine c ab is defined asT⎡C0⎤T e = ⎢ ⎥ with⎣0C ⎦⎡c⎢C = ⎢c⎢⎣c( a , b)~c ab = cos ∠The first part of the element stiffness matrix can be transformed as followsT⎡CK1e= ⎢⎣ 0⎡ T ~C Kii= ⎢T ~⎢⎣− C K1, eii1,e⎡ ~0 ⎤ Kii1,e⎥⎢T ~C ⎦⎢⎣− Kii1,T ~C − C KT ~C C Keii1,ii1,e~− K~K⎤eC⎥C ⎥⎦and similarly for the second part we getKii1,eii1,e⎤⎡C⎥⎢⎥⎦⎣0⎡ T ~C Kii= ⎢T ~⎢⎣− C Kxxyxzx⎡T ~0⎤C Kii⎥ = ⎢T ~C⎦⎢⎣− C KCT ~− C K2, eii 2,2 eT ~ii 2, eCC Kii2, eWe can substitute the explicit form of the matrices and get1, eii1,eccc⎤eC⎥C ⎥⎦xyyyzycccxzyzzz⎤⎥⎥⎥⎦T ~− C KT ~C Kii1,eii1,e⎤⎡C⎥⎢⎥⎦⎣00⎤⎥ =C⎦T ~C K=ii1,eC =2⎡ cxxEA ⎢⎢cxxcL0⎢⎢c⎣xxcEALyxzx0⎡c⎢⎢c⎢⎣ccxx yx2cyxczxxxyxzxccyxcccxyyyzyccxxccccczxxzyzzzzx yx2czx⎤⎡1⎥⎢⎥⎢0⎥⎦⎢⎣0⎤⎥⎥⎥⎥⎦0000⎤⎡c⎥⎢0⎥⎢c0⎥⎦⎢⎣cxxxyxzcccyxyyyzccczxzyzz⎤⎥⎥ =⎥⎦EAL0⎡c⎢⎢c⎢⎣cxxyxzx0000⎤⎡c⎥⎢0⎥⎢c0⎥⎦⎢⎣cxxxyxzcccyxyyyzccczxzyzz⎤⎥⎥ =⎥⎦T ~C K=NLii 2, e⎡⎢⎢⎢⎢⎣C =NL⎡c⎢⎢c⎢⎣cxxyxzxcccxyyyzycccxzyzzz⎤⎡0⎥⎢⎥⎢0⎥⎦⎢⎣00⎤⎡c⎥⎢0⎥⎢c1⎥⎦⎢⎣c⎤⎥⎥ =⎥⎦2 2( c ) ( ) ( ) ⎤xy + cxzcxycyy+ cxzcyz cxyczy+ cxzczz2 2( cxycyy+ cxzcyz) ( cyy+ cyz) ( cyyczy+ cyzczz)2 2( c + ) ( + ) ( + ) ⎥ ⎥⎥⎥ xy czycxzczzcyyczycyzczzczyczz⎦010xxxyxzThe elements of the second submatrix can be rewritten if the orthogonality conditions for thedirection cosines are used. We have for instance:cccyxyyyzccczxzyzzNL⎡0⎢⎢0⎢⎣0cccxyyyzycccxzyzzz⎤⎡c⎥⎢⎥⎢c⎥⎢⎦⎣cxxxyxzcccyxyyyzccczxzyzz⎤⎥⎥ =⎥⎦c2 2 2xx + cxy+ cxz= 1so the first diagonal term can be given asc2xy+ c2xz=21−cxxThere is also

cxxcyx+ cxycyy+ cxzcyz= 0so the first off-diagonal term can be given ascxycyy+ cxzcyz= −cxxcyxUsing the similar relations the entire second part of the stiffness matrix can be rewritten and finallywe getKe⎡ Kii= ⎢⎣−K1, eii1,e− KKii1,eii1,e⎤ ⎡ Kii⎥ + ⎢⎦ ⎣−K2, eii 2, e− KKii 2, eii 2, e⎤⎥⎦where:KKii 2, eii1,e==NL2⎡ cxxEA ⎢⎢cxxcL0⎢⎢c⎣xxcyxzx2( 1−c )⎡⎢⎢−c⎢⎢−c⎣xxxxxxccyxzxcxx yx2cyxc− czxccyxxx yx2( 1−cyx)− cyxcczxccxxcczxzx yx2czx− c− cxx⎤⎥⎥⎥⎥⎦cczx⎤yx zx( )⎥ ⎥⎥ 21−czx⎥ ⎦Thus we have expressed the stiffness matrix in terms of direction cosines between the local axis x ~and the global axes x, y and z. Because of such a relatively simple form, usually the elementmatrices are directly given in the global co-ordinates using the co-ordinates of nodes. Let usconsider the elementxyx iz iy iiy kx ke z Lkkzx ~The cosines required to express the element stiffness matrix can be given ascccxxyxzx= cos ∠= cos ∠= cos ∠( x,x~ )( y,x~ )( z,x~ )xk− xi=Ly k − y i=Lzk− zi=LThus, with these definitions there is no necessity for the transformation of co-ordinates.After the assembly of the global stiffness matrix K and inclusion of support conditions the global setof equations is formulatedKq = PThe global stiffness matrix has the dimension n×n, where n = 3s and s is the number of free(unsupported) nodes.

Solution of this equation gives the nodal displacements in the vector q. Then the equilibriumconditions in the deformed configuration must be checked.The new co-ordinates of nodes are obtained fromx ' = x + uiy ' = yiiz ' = z + wx ' = xkkkiikiky ' = ykz ' = zand the displacements u i , v i and w i come from q.The current length of the element is:i+ vii+ u+ vk+ wkkso the length increment isL'=( x ' −x') 2 + ( y ' −y') 2+ ( z ' −z' ) 2kikiki∆ L'=The current value of the axial force in the element is222( xk' −xi') + ( y k ' −yi ') + ( zk' −zi') − L0N' = N + ∆N'where the current force increment is obtained from the Hooke’s law∆L'∆ N'= EA Having found the current axial forces we can calculate the out-of-balance nodalL0forces ∆Q x ', ∆Q y ' and ∆Q z ' assembled into a vectorQ y 'Q x ' x⎡∆Qx' ⎤m⎢ ⎥∆Q ' =⎢∆Qy'Q⎥z 'N r 'N r ' = −∑N e ' ce = 1⎢⎣∆Q' ⎥yz ⎦Let us denote the resultant from the axial forces in the m-elements coinciding at a node as N r '.Then, using the equilibrium conditions at the node we getor in the matrix notationwhere⎡Q⎢Q ' =⎢Q⎢⎣Qxyz' ⎤⎥'⎥' ⎥⎦Q ' +xQ ' +yQ ' +zzm∑e = 1m∑e = 1m∑e = 1N ' cos ∠eN ' cos ∠eN ' cos ∠eQ ' = −⎡cos∠⎢c = ⎢cos∠⎢⎣cos∠m∑ N ee = 1( x,x~ )( y,x~)= 0= 0( z,x~ ) = 0' c( x,x~) ⎤ ⎡cxx ⎤⎥( )⎢y,x~⎥ =⎢cyx( ) ⎥ ⎢ ⎥ ⎥⎥ z,x~⎣czx⎦⎦

The external forces at the nodes areP ' P + P= 0where P 0 is the vector of initial (tightening) nodal forces and P is the vector of external imposedloads.The out-of-balance forces arem0 ∑N e 'e=1∆Q'= P'−Q'= P + P +In the next iteration the equilibrium equation readsK'∆ q'= ∆Q'Solving of these equations yields the vector of displacement increments, which are used tocalculate the new values of current displacementsq' = q + ∆q'From this point the calculations are repeated to get the new values of out-of-balance forces, etc.The iterations stop when the current value of the out-of-balance forces falls below a tolerance∆Q ' ≤ tolcThe presented algorithm follows the line of the Newton method. Let us now briefly present themethods of iterative solving of non-linear equations.The Newton methodP∆Q'- a new stiffness matrix at each iterationPQ'qq ∆q' ∆q''q realThe modified Newton methodPP∆Q'Q'q∆q'q realq- the initial stiffness matrix used at eachiteration- slower convergence but low computationcost at each iteration

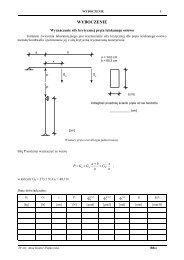
The Newton-Raphson methodPP 3P 2P- loading divided into increments- much better convergence in highly nonlinearcasesP 1q5. ExampleWe consider a plane cable system consisting of 3 elements.Initial configurationHAR Ay1xCP 02DP 033 4 3BR BH3Node co-ordinates:x A = 0.0y A = 0.0x B = 10.0y B = 0.0x C = 3.0y C = 3.0x D = 7.0y D = 3.0Data:EA = 8000 kNInitial tightening load – two nodal forces P 0 = 5 kNThe reactions in the initial configuration are∑M B∑: 10R− 5 ⋅ 7 − 5 ⋅ 3 = 0 ⇒ RAM CA =∑y : RB = 5kN: 3RA − 3H= 0 ⇒ H = 5kNThe axial forces in the inclined cables can be obtained from the equilibrium of the node A or B5kNHAR AN 1∑2y : N = 5kN ⇒ N121 =7.07107kNAnd from the symmetry N 3 = N 1 .The force in the cable CD comes from the equilibrium of the node CN 1 CN 2P 0∑x22: N1 = N2⇒ N2=5kN

The cable system in this configuration is now loaded by a set of two external loads P = 12 kNA xBH13H3R AC 2 DR ByP 0P 0P P3 4 3Initial lengths for the elements are22( 3 − 0) + ( 3 − 0) = 4.24264 L0,3L =0,1=mThe direction cosines are:ccLxx,1yx,122( 7 − 3) + ( 3 − 3) 4.0m0 ,2 ==xC− x=Ly=C0,1− yL0,1AA3 − 0= = 0.7071074.242643 − 0= = 0.7071074.24264ccxx,2yx,2xD− x=L0,2yD− y=L0,2CC7 − 3= = 1.04.03 − 3= = 0.04.0The element stiffness matricesK=AA,1=EAL0,180004.24264⎡0.5⎢⎣0.5cc⎡ c⎢⎢⎣cxxcxx,3yx,32xx,1,1 yx,1xB− x=L0,3yB− y=Lc0.5⎤⎥ +0.5⎦K0,31DD10 − 7= = 0.7071074.24264⎡ K= ⎢⎣−Kcxx,1yx,12cyy,10 − 3= = −0.7071074.24264AA,1AA,1⎤ N⎥ +⎥⎦L7.071074.2426410,1⎡ 0.5⎢⎣−0.5− KKAA,1AA,1⎤⎥⎦2( 1−c )⎡⎢⎢⎣− cxx,1cxx,1yx,1− ccxx,1yx,12( 1−cyy,1)− 0.5⎤⎡943.643⎥ = ⎢0.5 ⎦ ⎣941.976⎤⎥ =⎥⎦941.976⎤⎥943.643⎦K2⎡ K= ⎢⎣−KAA,2AA,2− KKAA,2AA,2⎤⎥⎦

K=AA,2=EAL0,28000 ⎡1⎢4.0 ⎣0⎡ c⎢⎢⎣cxx0⎤⎥ +0⎦2xx,2c,2 yx,254.0⎡0⎢⎣0ccxx,2yx,22cyy,2⎤ N⎥ +⎥⎦L20,20⎤⎡2000.0⎥ = ⎢1⎦⎣ 02( 1−c )⎡⎢⎢⎣− cxx,20 ⎤⎥1.250⎦xx,2cyx,2− ccxx,2yx,22( 1−cyy,2)⎤⎥ =⎥⎦K=AA,3=EAL0,380004.24264⎡ c⎢⎢⎣cxx⎡ 0.5⎢⎣−0.52xx,3c,3 yx,3cK− 0.5⎤⎥ +0.5 ⎦3c⎡ K= ⎢⎣−Kxx,3yx,32cyy,3AA,3AA,3⎤ N⎥ +⎥⎦L7.071074.2426430,3⎡0.5⎢⎣0.5− KKAA,3AA,3⎤⎥⎦2( 1−c )⎡⎢⎢⎣− cxx,3xx,3cyx,3− ccxx,3yx,32( 1−cyy,3)0.5⎤⎡ 943.643⎥ = ⎢0.5⎦⎣−941.976⎤⎥ =⎥⎦− 941.976⎤⎥943.643 ⎦The pattern of global stiffness matrix assembly and support conditions inclusion isK =ACDBA C D BK 1K 2K 3and the remaining fragment of the matrix K corresponds to the free nodes C and D.This remaining fragment is⎡2943.64⎢⎢941.976K =⎢−2000.0⎢⎣ 0.0941.976944.8930.0−1.250− 2000.00.02943.64− 941.9760.0 ⎤⎥−1.250⎥− 941.976⎥⎥944.893 ⎦The load vector corresponding to the free nodes C and D has two forces P in the y direction andzero forces in the x directionThe solution of the equilibrium equation⎡ 0.0 ⎤⎢ ⎥⎢12.0P = ⎥⎢ 0.0 ⎥⎢ ⎥⎣12.0⎦Kq = P is⎡− 0.0029922⎤⎢⎥⎢0.0157036q =⎥⎢ 0.0029922 ⎥⎢⎥⎣ 0.0157036 ⎦Now we can find the new co-ordinates of free nodes

The current element lengths arexyyCCDD' = 3.0 − 0.0029922 = 2.99701' = 3.0 + 0.0157036 = 3.01570x ' = 7.0 + 0.0029922 = 7.00299' = 3.0 + 0.0157036 = 3.0157022( 2.99701−0.0) + ( 3.01570 − 0.0) = 4.25165m 'L =1' =L322( 7.00299 − 2.99701) + ( 3.01570 − 3.01570) 4.00598mL 2 ' ==The length increments are∆ L 0,1'= 4.25165 − 4.24264 = 0.00901m= ∆L0,3'∆ L 0 ,2 ' = 4.00598 − 4.0 = 0.00598mThe increments of axial forces∆L0,1'0.00901∆ N1' = EA = 8000 ⋅ = 16.9894kN = ∆N3'L4.24264∆N0,1∆L' = EAL' 0.00598= 8000 ⋅4.00,22 =0,211.9680kNand the current values of the axial forcesN 1' = N1+ ∆N1'= 7.07107 + 16.9894 = 24.0605kN = N3'N ' = N + ∆N2 ' = 5.0 + 11.96802 2=The current values of the direction cosines areccccxx,1yx,1xx,3yx,32.99701−0== 0.7049054.251653.01570 − 0== 0.7093014.25165ccxx,2yx,2= 1.0= 0.016.9680kN10 − 7.00299== 0.7049054.251650 − 3.01570== −0.7093014.25165The out-of-balance forces can be found from the equilibrium of nodes24.0605 C16.96805 + 12x∆Q∆Qxy' = −24.0605⋅ 0.704905 + 16.9680 = 0.00763kN' = −24.0605⋅ 0.709301+12 + 5 = −0.06614kNy

And similarly, from the equilibrium of the node D we getto complete the vector∆Q∆Qxy' = −0.00763kN' = −0.06614kN⎡ 0.00763 ⎤⎢ ⎥⎢− 0.06614∆Q' =⎥⎢−0.00763⎥⎢ ⎥⎣−0.06614⎦The stiffness matrices in the current configuration are formed using the following submatricesK=K=EA ⎡ c= ⎢L0,1⎢⎣cxx8000 ⎡0.496891⎢4.24264 ⎣ 0.50⎤ N ⎡1'⎥ + ⎢⎥⎦L1'⎢⎣− c2( 1−c )2xx,1cxx,1cyx,1xx,1− c cAA,1' 22,1cyx,1cyy,1xx,1cyx,1⎡⎢⎣K=EA ⎡ c= ⎢L0,3⎢⎣cxx80004.24264xx,1yx,1( 1−cyy,1)0.50 ⎤ 24.0605 ⎡0.503108⎥ + ⎢0.503108⎦4.25165 ⎣ − 0.50EA ⎡ c= ⎢L0,2⎢⎣cxx8000 ⎡1⎢4.0 ⎣00⎤⎥ +0⎦16.96804.00598⎡0⎢⎣0⎤ N ⎡2'⎥ + ⎢⎥⎦L2' ⎢⎣− c0⎤⎡2000.0⎥ = ⎢1⎦⎣ 0⎤⎥ =⎥⎦− 0.50 ⎤ ⎡939.794⎥ = ⎢0.496891⎦⎣939.9802( 1−c )2xx,2cxx,2cyx,2xx,2− c cAA,2' 22,2cyx,2cyy,2xx,2cyx,20.496891− 0.50⎤ N ⎡3'⎥ + ⎢⎥⎦L3' ⎢⎣− c2( 1−c )2xx,3cxx,3cyx,3xx,3− c cAA,3 '22,3cyx,3cyy,3xx,3cyx,3− 0.50 ⎤ 24.0605 ⎡0.503108⎥ + ⎢0.503108⎦4.25165 ⎣ 0.50xx,3yx,3( 1−cyy,3)0 ⎤⎥4.23567⎦⎤⎥ =⎥⎦xx,2yx,2( 1−cyy,2)⎤⎥ =⎥⎦0.50 ⎤ ⎡ 939.794⎥ = ⎢0.496891⎦⎣−939.980939.980⎤⎥951.482⎦− 939.980⎤⎥951.482 ⎦Following the same assembly and support conditions pattern we get the “active” part of the globalstiffness matrix in the form⎡2939.79⎢⎢939.980K ' =⎢−2000.0⎢⎣ 0.0939.980955.7180.0− 4.23567− 2000.00.02939.79− 939.980and solving the equilibrium equations with out-of-balance forceswe get the following increments of displacementsK'∆ q'= ∆Q'⎡ 0.0000182 ⎤⎢⎥⎢− 0.0000875∆q' =⎥⎢−0.0000182⎥⎢⎥⎣−0.0000875⎦With these values the total current displacements can be found0.0 ⎤⎥− 4.23567⎥− 939.980⎥⎥955.718 ⎦

⎡u⎢⎢v⎢u⎢⎣vCCDD' ⎤ ⎡−0.0029922 + 0.0000182⎤⎡− 0.0029738⎤⎥'⎢⎥ ⎢⎥⎥ ⎢0.0157037 − 0.0000852⎥ = ⎢0.0156162= ∆q'+ q =⎥' ⎥ ⎢ 0.0029922 − 0.0000182 ⎥ ⎢ 0.0029738 ⎥⎥ ⎢⎥ ⎢⎥' ⎦ ⎣ 0.0157037 − 0.0000852 ⎦ ⎣ 0.0156162 ⎦The co-ordinates of nodes in the current deformed configurationThe current element lengths areThe length increments areThe increments of axial forcesand the current values of the axial forcesxyyCCDD' ' = 3.0 − 0.0029738 = 2.997026' ' = 3.0 + 0.0156162 = 3.016162x ' ' = 7.0 + 0.0029738 = 7.002974''= 3.0 + 0.0156162 = 3.016162L 1' ' = 4.251600m = L3''L 2 ' ' =4.005948m∆ L0 ,1' ' = 0.008960m = ∆L0,3''∆L 0 ,2 ' ' =0.005948m∆ N1' ' = 16.8951kN = ∆N3''∆N''2 =The current values of the direction cosines are11.8960kNN 1' ' = N1+ ∆N1'' = 23.9662kN = N3''N 2 ''= N2+ ∆N2'' = 16.8960kNccxx,1yx,1cc= 0.704917= 0.709290xx,2yx,2= 1.0= 0.0ccxx,3yx,3= 0.704917= −0.709290The current out-of-balance forces can be found from the equilibrium of nodes23.9662 C16.89605 + 12x∆Q∆Qxy''= −23.9662⋅ 0.704917 + 16.8960 = 0.00182kN''= −23.9662⋅ 0.709290 + 12 + 5 = 0.00101kNy

These values are several times smaller than the out-of-balance forces in the first iteration, whatconfirms the convergence behaviour of the solution process.They are also relatively small compared to the current values of forces in the elements (about0.001%), so the iterations can be stopped at this point.