Modeling of Mechanical (Lumped Parameter) Elements

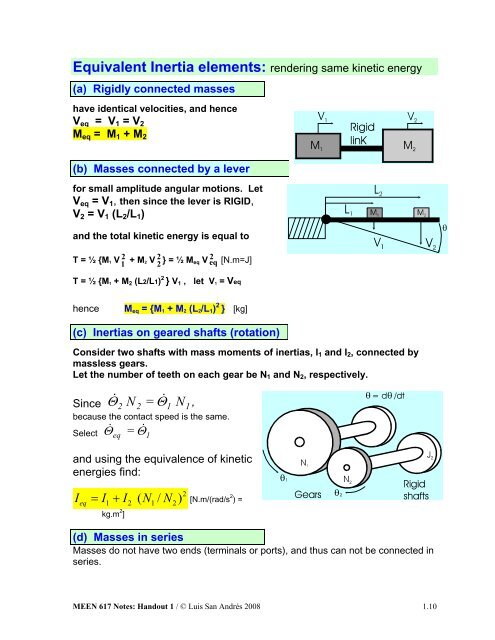
Equivalent Inertia elements: rendering same kinetic energy(a) Rigidly connected masseshave identical velocities, and henceV eq = V 1 = V 2M eq = M 1 + M 2(b) Masses connected by a leverfor small amplitude angular motions. LetV eq = V 1 , then since the lever is RIGID,V 2 = V 1 (L 2 /L 1 )and the total kinetic energy is equal toT = ½ {M 1 V21+ M2 V22} = ½ Meq V2 eq [N.m=J]T = ½ {M 1 + M 2 (L2/L1) 2 } V 1 , let V 1 = VeqhenceM eq = {M 1 + M 2 (L 2 /L 1 ) 2 } [kg](c) Inertias on geared shafts (rotation)Consider two shafts with mass moments of inertias, I 1 and I 2 , connected bymassless gears.Let the number of teeth on each gear be N 1 and N 2 , respectively.Since Θ = N ,2 N 2 Θ11because the contact speed is the same.ΘΘSelect eq = 1and using the equivalence of kineticenergies find:I I I N N2eq=1+ 2(1/ 2)[N.m/(rad/s 2 ) =kg.m 2 ](d) Masses in seriesMasses do not have two ends (terminals or ports), and thus can not be connected inseries.MEEN 617 Notes: Handout 1 / © Luis San Andrés 2008 1.10