WUCT121 Discrete Mathematics Logic Tutorial Exercises Solutions

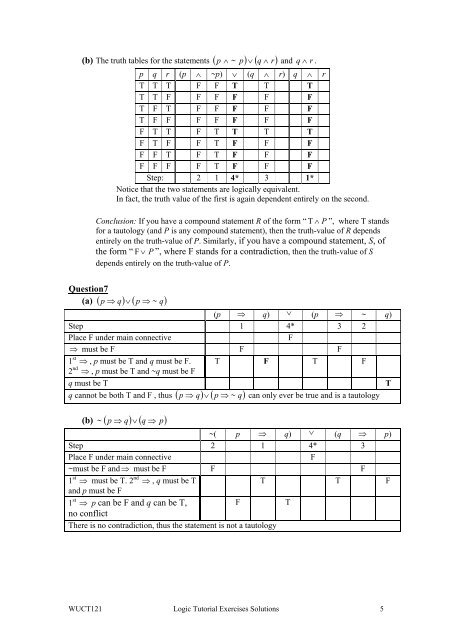
(b) The truth tables for the statements ( p p) ∨ ( q ∧ r)∧ ~ and q ∧ r .p q r (p ∧ ~p) ∨ (q ∧ r) q ∧ rT T T F F T T TT T F F F F F FT F T F F F F FT F F F F F F FF T T F T T T TF T F F T F F FF F T F T F F FF F F F T F F FStep: 2 1 4* 3 1*Notice that the two statements are logically equivalent.In fact, the truth value of the first is again dependent entirely on the second.Conclusion: If you have a compound statement R of the form “ T ∧ P ”, where T standsfor a tautology (and P is any compound statement), then the truth-value of R dependsentirely on the truth-value of P. Similarly, if you have a compound statement, S, ofthe form “ F ∨ P ”, where F stands for a contradiction, then the truth-value of Sdepends entirely on the truth-value of P.Question7(a) ( p ⇒ q) ∨ ( p ⇒ ~ q)(p ⇒ q) ∨ (p ⇒ ~ q)Step 1 4* 3 2Place F under main connectiveF⇒ must be F F F1 st ⇒ , p must be T and q must be F. T F T F2 nd ⇒ , p must be T and ~q must be Fq must be TTp ⇒ q ∨ p ⇒ ~ q can only ever be true and is a tautologyq cannot be both T and F , thus ( ) ( )(b) ~ ( p ⇒ q) ∨ ( q ⇒ p)~( p ⇒ q) ∨ (q ⇒ p)Step 2 1 4* 3Place F under main connectiveF~must be F and ⇒ must be F F F1 st ⇒ must be T. 2 nd ⇒ , q must be TT T Fand p must be F1 st ⇒ p can be F and q can be T,FTno conflictThere is no contradiction, thus the statement is not a tautologyWUCT121 Logic Tutorial Exercises Solutions 5