DETERMINANTS AND EIGENVALUES 1. Introduction Gauss ...

More documents

Recommendations

Info

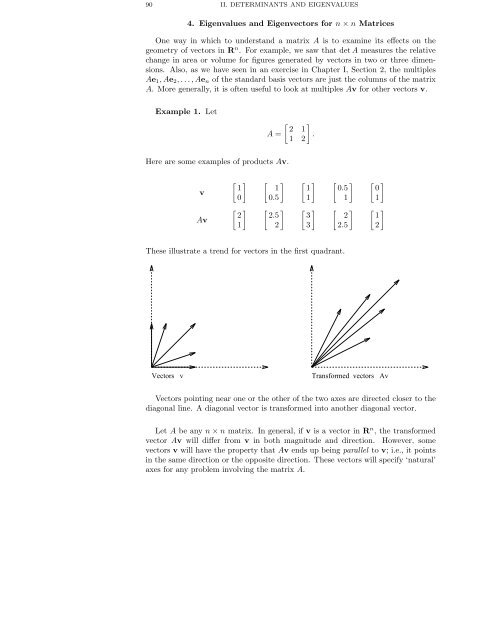
90 II. DETERMINANTS AND EIGENVALUES4. Eigenvalues and Eigenvectors for n × n MatricesOne way in which to understand a matrix A is to examine its effects on thegeometry of vectors in R n . For example, we saw that det A measures the relativechange in area or volume for figures generated by vectors in two or three dimensions.Also, as we have seen in an exercise in Chapter I, Section 2, the multiplesAe 1 ,Ae 2 ,...,Ae n of the standard basis vectors are just the columns of the matrixA. More generally, it is often useful to look at multiples Av for other vectors v.Example 1. LetA =[ ]2 1.1 2Here are some examples of products Av.vAv[ ] [ [ [ [ ]1 1 1 0.5 00 0.5]1]1]1[ ] [ ] [ ] [ [ ]2 2.5 3 2 11 2 3 2.5]2These illustrate a trend for vectors in the first quadrant.Vectors vTransformed vectors AvVectors pointing near one or the other of the two axes are directed closer to thediagonal line. A diagonal vector is transformed into another diagonal vector.Let A be any n × n matrix. In general, if v is a vector in R n , the transformedvector Av will differ from v in both magnitude and direction. However, somevectors v will have the property that Av ends up being parallel to v; i.e., it pointsin the same direction or the opposite direction. These vectors will specify ‘natural’axes for any problem involving the matrix A.
4. EIGENVALUES AND EIGENVECTORS FOR n × n MATRICES 91vvAVPositive eigenvalueAvNegative eigenvalueVectors are parallel when one is a scalar multiple of the other, so we make thefollowing formal definition. A non-zero vector v is called an eigenvector for thesquare matrix A if(1) Av = λvfor an appropriate scalar λ. λ is called the eigenvalue associated with the eigenvectorv.In words, this says that v ≠ 0 is an eigenvector for A if multiplying it by A hasthe same effect as multiplying it by an appropriate scalar. Thus, we may thinkof eigenvectors as being vectors for which matrix multiplication by A takes on aparticularly simple form.It is important to note that while the eigenvector v must be non-zero, the correspondingeigenvalue λ is allowed to be zero.Example 2. LetA =[ ]2 1.1 2We want to see if the system[ ][ ] [ ]2 1 v1 v1=λ1 2 v 2 v 2has non-trivial solutions v 1 ,v 2 . This of course depends on λ. If we write this systemout, it becomesor, collecting terms,In matrix form, this becomes(2)2v 1 + v 2 = λv 1v 1 +2v 2 =λv 2(2 − λ)v 1 + v 2 =0v 1 +(2−λ)v 2 =0.[ ]2 − λ 1v = 0.1 2−λ
Page 4 and 5: 74 II. DETERMINANTS AND EIGENVALUES
Page 6 and 7: 76 II. DETERMINANTS AND EIGENVALUES
Page 8: 78 II. DETERMINANTS AND EIGENVALUES
Page 11 and 12: 2. DEFINITION OF THE DETERMINANT 81
Page 13 and 14: 3. SOME IMPORTANT PROPERTIES OF DET
Page 19: 4. SOME IMPORTANT PROPERTIES OF DET
Page 23 and 24: 4. EIGENVALUES AND EIGENVECTORS FOR
Page 31 and 32: 5. DIAGONALIZATION 101are eigenvect
Page 33 and 34: 5. DIAGONALIZATION 103Example 3. Co
Page 35 and 36: 6. THE EXPONENTIAL OF A MATRIX 1053
Page 37 and 38: 6. THE EXPONENTIAL OF A MATRIX 107(
Page 39 and 40: 7. REVIEW 109⎡3. A = ⎣ 0 1 1⎤

DETERMINANTS AND EIGENVALUES 1. Introduction Gauss ...

Create successful ePaper yourself

Delete template?

Save as template?