Final Exam Solution - King Fahd University of Petroleum and Minerals

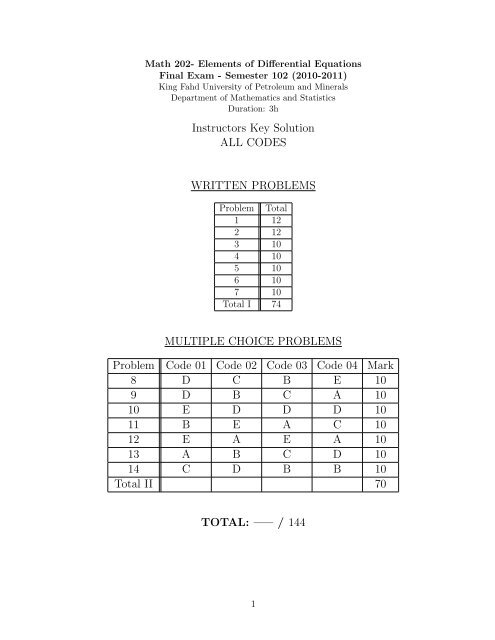
Math 202- Elements of Differential EquationsFinal Exam - Semester 102 (2010-2011)King Fahd University of Petroleum and MineralsDepartment of Mathematics and StatisticsDuration: 3hInstructors Key SolutionALL CODESWRITTEN PROBLEMSProblem Total1 122 123 104 105 106 107 10Total I 74MULTIPLE CHOICE PROBLEMSProblem Code 01 Code 02 Code 03 Code 04 Mark8 D C B E 109 D B C A 1010 E D D D 1011 B E A C 1012 E A E A 1013 A B C D 1014 C D B B 10Total II 70TOTAL: —– / 1441

Exercise 1 (12 points)Consider the following differential equationy ′′ − 2xy ′ + 4y = 0.Find the power series solutions about the ordinary point x = 0.Solutiony = ∑ ∞n=0 C nX n , y ′ = ∑ ∞n=1 C nX n−1 , y ′′ = ∑ ∞n=2 n(n − 1)C nX n−2 (1 point)Substituting in the DE gives:∑ ∞n=2 n(n − 1)C nX n−2 − ∑ ∞n=1 2nC nX n + ∑ ∞n=0 4C nX n = 0. (2 points)With k = n−2 we have, ∑ ∞n=2 n(n−1)C nX n−2 = ∑ ∞k=0 (k+2)(k+1)C k+2X k . (1 point)Thus ∑ ∞k=0 (k + 2)(k + 1)C k+2X k − ∑ ∞k=1 2kC kX k + ∑ ∞k=0 4C kX k = 0. (2 points)Hence, (2C 2 + 4C 0 ) + ∑ ∞k=1 [(k + 2)(k + 1)C k+2 − 2kC k + 4C k ] X k = 0. (2 points)Which gives:2C 2 + 4C 0 = 0, (1 point)and(k + 2)(k + 1)C k+2 − (2k − 4)C k = 0, for k = 1, 2, ... (1 point)Thus C 2 = −2C 0 and C k+2 =(2k−4)(k+1)(k+2) C k, for k = 1, 2, ...Finally y(x) = C 0 + C 1 x − 2C 0 x 2 − 1 3 C 1x 3 − 130 C 1x 5 + ... (2 points)or also y(x) = C 0 (1 − 2x 2 ) + C 1 (x − 1 3 x3 − 130 C 1x 5 + ...).2

Exercise 2 (12 points)Consider the following differential equationa) Find the indicial equation roots.x 2 y ′′ − xy ′ + 5 (x − 1)y = 0.4b) Let y 1 = ∑ n≥0 C nX n+r 1, with C 0 = 1 be the power series solution corresponding tothe largest root of the indicial equation. Find the value of C 1 + C 2 .Solutiona) The indicial equation is of the form r(r − 1) + a 0 r + b 0 = 0 with: (1 point)a 0 = lim x→0 x(− x ) = −1 and bx 2 0 = lim x→0 x 2 [ 5( x−1 )] = − 5 . (1 point)4 x 2 4The indicial equation is: r(r − 1) − r − 5 = 4 r2 − 2r − 5 = (r − 5)(r + 1 ) = 0. (1 point)4 2 2Hence r 1 = 5 > r 2 2 = − 1 . (1 point)2Total: 4 pointsb) We have r 1 = 5 2the largest root, theny 1 = ∑ ∞n=0 C nx n+ 5 2 , y ′ 1 = ∑ ∞n=0 (n + 5 2 )C nx n+ 3 2 and y ′′1 = ∑ ∞n=0 (n + 5 2 )(n + 3 2 )C nx n+ 1 2 .⇒ (1 point)Substituting in the DE gives:∑ ∞n=0 (n+ 3 2 )(n+ 5 2 )C nx n+ 5 2 − ∑ ∞n=0 (n+ 5 2 )C nx n+ 5 2 + 5 4∑ ∞n=0 C nx n+ 7 2 − 5 4∑ ∞n=0 C nx n+ 5 2 = 0⇒ (1 point)Thus ∑ ∞[n=0 (n +3)(n + 5) − (n + 5) − ∑ 52 2 2 4]Cn x n+ 5 2 + 5 ∞4 m=1 C m−1x m+ 5 2 = 0.⇒ (1 point)Hence, 0 + ∑ ∞n=1 [n(n + 3)] C nx n+ 5 2 + 5 4∑ ∞n=1 C n−1x n+ 5 2 = 0. ⇒ (1 point)Finally we have ∑ ∞[n=1 n(n + 3)Cn + 5C ]4 n−1 xn+ 5 2 = 0. ⇒ (2 points)The recurrence relation is: C n = − 54n(n+3) C n−1, for n = 1, 2, ... ⇒ (1 point)With C 0 = 1 we get C 1 = − 516 and C 2 = 5128 .The value of C 1 + C 2 is − 35 . ⇒ (1 point)128Total: 8 points3

Exercise 3 (10 points)Find the solution of the following initial value problem( )( 1 −2−1X ′ =X, X(0) =3 −42).SolutionFirst we need to find the determinant of (A − λI).∣ 1 − λ −23 −4 − λ ∣ = (1 − λ)(−4 − λ) + 6 = λ2 + 3λ + 2. ⇒ (1 point)The characteristic equation is then λ 2 + 3λ + 2 = 0.The eigenvalues of A are λ 1 = −2 and λ 2 = −1. ⇒ (1 point)For λ 1 = −2:( ) ( )3 −2 | 0 3 −2 | 0(A − λI)K = 0 ⇒⇒⇒ (1 point)3 −2 | 0 0 0 | 0( 2)Let k 2 = r then k 1 = 2r and the eigenvector K 3 1 = r3. ⇒ (1 point)1For λ 2 = −1:(A − λI)K = 0 ⇒( 2 −2 | 03 −3 | 0) ( )2 −2 | 0⇒⇒ (1 point)0 0 | 0). ⇒ (1 point)( 1Let k 2 = s then k 1 = s and the eigenvector K 2 = s1Then the general solution is X(t) = c 1( 231)e −2t + c 2( 11)e −t ⇒ (1 point)To satisfy the initial condition, we get 2 3 c 1 + c 2 = −1 and c 1 + c + 2 = 2. ⇒ (1 point)Therefore c 1 = 9 and c 2 = −7.⇒ (1 point)( 6Finally, the solution of the IVP is X(t) =9) ( −7e −2t +−7)e −t ⇒ (1 point)4

Exercise 4 (10 points)Solve the following differential equation using an appropriate substitution:Solutiondydx = y2 + 2xyx 2 .Let y = ux, then dy = x du + u. ⇒ (2 points)dx dxSubstitution in the DE gives: x du + u = u2 x 2 +2ux 2dx x 2= u 2 + 2u ⇒ (1 point)Therefore du = u2 +udx xwhich is separable. ⇒ (1 point)We obtaindu= dx ⇒ ( 1 − 1 )du = dx . ⇒ (2 points)u(u+1) x u u+1 xThus ln |u| − ln |u + 1| = ln |x| + ln c ⇒ ln | u | = ln |cx|.⇒ (1 point)u+1Henceu= xc ⇒ 1 − xu+1 x+y= xc. ⇒ (2 points)Finally y = cx21−cx . ⇒ (1 point) 5

Exercise 5 (10 points)Let y 1 = x be a solution of the Homogeneous differential equation :x 2 y ′′ − (x 2 + 3x)y ′ + (x + 3)y = 0.Find a second solution y 2 (x) linearly independent from y 1 .SolutionFirst we write the standard form y ′′ − (1 + 3 x )y′ + x+3 y = 0. ⇒ (2 points)x 2Then P (x) = −(1 + 3 ). ⇒ (1 point)x∫Hence y 2 = y e − ∫ P (x)dx1 dx ⇒ (2 points)y12y 2 = x ∫ ex+3 ln xdx = x ∫ x 3 e xdx. ⇒ (3 points)x 2x 2We then have y 2 = x ∫ xe x dx = x(xe x − e x ) = x 2 e x − xe x . ⇒ (2 points)6

Exercise 6 (10 points)a) Show that the functions f 1 = e x cos x and f 2 = e x sin x constitute a fundamentalset of solutions of the homogeneous differential equation 3y ′′ − 6y ′ + 6y = 0.b) Find the particular solution of the differential equation 3y ′′ − 6y ′ + 6y = e x sec x.Solutiona) The wronskian of f 1 and f 2 is W =∣e x cosxe x cosx − e x sinxe x sinxe x sinx + e x cosx∣⇒ (1 point)W = e 2x sinxcosx + e 2x cos 2 x − e 2x sinxcosx + e 2x sin x = e 2x ≠ 0. ⇒ (1 point)Therefore f 1 and f 2 are two linearly independent solutions of the second order homogeneousdifferential equation. ⇒ (1 point)We deduce that f 1 and f 2 form a fundamental set of solutions. ⇒ (1 point)Total: (4 points)b) We use variation of parameters: y p = u 1 y 1 + u 2 y 2 . ⇒ (1 point)Let W 1 =∣0 e x sinx13 ex secx e x sinx + e x cosx∣ = − 1 3 e2x tanx. ⇒ (1 point)Then u ′ 1 = W 1W= − 1tanx. Therefore u 3 1 = 1 ln |cosx|. ⇒ (1 point)3Let W 2 =∣e x cosx 0e x cosx − e x sinx1 3 ex secx∣ = 1 3 e2x . ⇒ (1 point)Then u ′ 2 = W 2W= 1. Therefore u 3 2 = 1 x. ⇒ (1 point)3Thus y p = 1 3 ex (cosx ln |cosx| + xsinx). ⇒ (1 point)Total: (6 points)7

Exercise 7 (10 points)Consider the system of differential equations( tX ′ = AX +t).Let φ(t) =system.( −2 e3t1 e 3t )be the fundamental matrix of the associated homogeneousFind the general solution of this system.SolutionThe general solution of the system should be written:X(t) = φ(t)c + X p (t), with c = (c 1 , c 2 ) t . ⇒ (1 point)We have |φ(t)| = −3e 3t . Thus φ −1 = − 1 3 e−3t ( e3tX p (t) = φ ∫ φ −1 F (t)dt = φ ∫ − 1 3 e−3t ( e3tX p (t) = φ ∫ ( ) 0− 1 3 e−3t dt =−3t( ) ()−2 e3t0X p (t) =1 e 3t − 1 3 te−3t − 1 =9 e−3tFinally X(t) = φ(t)c +( −13 t − 1 9− 1 3 t − 1 9−e 3t). ⇒ (2 points)−1 −2) ( )−e 3t tdt ⇒ (2 points)−1 −2 t( ) ( )−2 e3t ∫ 01 e 3t te −3t dt ⇒ (2 points)( −13 t − 1 9− 1 3 t − 1 9). ⇒ (1 point)). ⇒ (2 points)8

Exercise 8If we convert the Cauchy-Euler equation −2x 2 y ′′ + xy ′ − 2y = 0 into a second orderdifferential equation with constant coefficients y ′′ + ay ′ + by = 0 thena + b =A) − 1 2B) − 3 2C) 1 2D) − 1 3E) − 2 39

Exercise 9If the linear operator D 3 + aD 2 + bD + c annihilates (1 + e −x ) 2 thena + b + c =A) 5B) 4C) 3D) 6E) 210

Exercise 10The set {2x, x −1 , x −1 ln(x)} forms a fundamental set of solutions to the differentialequation x 3 y ′′′ + 4x 2 y ′′ + xy ′ − y = 0 on the interval (0, ∞).The Wronskian of {2x, x −1 , x −1 ln(x)} is:A) 8 x 4B) − 8 x 2C) 8 x 3D) 8 x 5E) − 8 x11

Exercise 11Consider the following differential equation( y2x − 2e3y)dx + (2yln(x) − 3e 3y )dy = 0.3 x x 2The integrating factor that makes the differential equation exact is:A) x 2B) xC) yD) y 2E) xy12

Exercise 12Which one of the following statements is TRUE about the ODEA) x = 0 is an irregular singular point.(x 4 − x 2 )y ′′ + (2x − 2)y ′ + (x 3 + x 2 )y = 0.B) x = 1 is an irregular singular point.C) x = −1 is an ordinary point.D) The singular points are x = 1 and x = −1 only.E) Every point, except x = 0, is an ordinary point.13

Exercise 13Given the system of differential equations⎛X ′ = AX, with A = ⎝2 −1 20 1 0−1 0 0Knowing that 1 and 1 + i are eigenvalues of A, Determine which of the functionsbelow is a solution of this system:⎛⎞1 + 10cos(t) + 10sin(t)A) ⎝ −1 ⎠ e t−1 − 10sin(t)⎛⎞10 + cos(t) + sin(t)B) ⎝ −10 ⎠ e −t−10 + sin(t)⎛10⎞C) ⎝ cos(t) ⎠ e tsin(t)⎛⎞1 + cos(t) − sin(t)D) ⎝ −1 ⎠ e −t−1 − cos(t)⎛⎞cos(t) + sin(t)E) ⎝ 11 − sin(t)⎞⎠⎠ e t 14

Exercise 14⎛Consider A = ⎝0 1 −10 0 20 0 0⎞⎠The matrix exponential e At is given by:⎛⎞1 t t 2 − tA) ⎝ 0 1 2t ⎠0 0 1⎛0 t t⎞B) ⎝ 0 0 2t ⎠0 0 0⎛0 −t t⎞C) ⎝ 0 0 −2t ⎠0 0 0⎛t t t⎞D) ⎝ −t 0 3t ⎠t 0 0⎛1 t 2t⎞E) ⎝ −3t 0 3t ⎠t 0 −t15