MAT 2355 Final Exam - Université d'Ottawa

MAT 2355 Final ExamDecember 20, 2005.Duration: 3 hoursFamily Name:First Name:Student number:123456TotalAdviceTake 5 minutes to read the entire paper before you begin to write, and read eachquestion carefully. Make a note of the questions you feel confident you can do, and thendo those first: you do not have to proceed through the paper in the given order.Instructions1. You have 3 hours to complete this exam.2. This is a closed book exam, and no notes of any kind are permitted. Calculators areallowed, but may only be used for computations and not for storage of data or text.The use of cell phones or any other text-storage devices is not permitted.3. The correct answer requires reasonable justification written legibly and logically –youmust convince me that you know why your solution is correct.4. Questions 1–6 are each worth an equal number of points. Questions 3, 4 and 5 havebonus parts worth in total an extra 10% of the paper and should not be tried untilall other parts of questions 1-6 have been completed and checked.5. Please use the space provided, including the backs of pages if necessary. If you needscrap paper, please ask.Good luck! Bonne chance!1

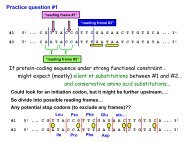
1. Consider the following 4 lines in the plane:L 1 = {(x, y) ∈ R 2 | x + y =0}L 2 = {(x, y) ∈ R 2 | y = −1}L 3 = {(x, y) ∈ R 2 | x − y =0}L 0 = {(x, y) ∈ R 2 | y =0}a) Sketch L 1 ,L 2 and L 3 carefully on the same set of labelled axes, and indicate thecoordinates of the point of intersection of L 2 and L 3 .b) Completely describe the isometry f = R L3 R L2 R L1 . Justify your answer. (You donot need to compute a formula for f: you may proceed by replacing R L3 R L2 byR L′3R L′2for appropriate new lines L ′ 2,L ′ 3, and then by replacing R L′2R L1 by R L′′ R2L ′ 1for appropriate new lines L ′′2,L ′ 1.)c) Using (b), or otherwise, completely describe the isometry g = fR L0 . Justify youranswer. (You do not need to compute a formula for g.)2

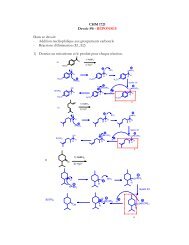
2. Let f : R 2 → R 2 be defined byf(v) = 1 5[ ] [ ]−3 4 2v + , for v ∈ R 2 .4 3 −1a) Show that f is an orientation reversing isometry of R 2 .b) Find the formula for f(f(v)), for v ∈ R 2 .c) Is f a reflection or a glide reflection? Give details for your response, including equationsfor any lines, and components for any vectors necessary for the complete description.4

3. Let H = {v ∈ R 3 | a · v = b} and K = {v ∈ R 3 | c · v = d} be planes in R 3 , whereb, d ∈ R are scalars, and a, c ∈ R 3 are both zero. Suppose that M is another plane in R 3which is not parallel to H or K.a) If P, Q are two points in H, give the vector parametric form for the line ←→ PQ.b) Show carefully that if P, Q are two points in H, then the line ←→ PQ is contained in H.c) Define what it means for two lines L 1 and L 2 in R 3 to be parallel. (Use the defintionfrom class: do not talk about their direction vectors.)d) Show that if H and K are parallel, then the lines M ∩ H and M ∩ K are also parallel.(Use the defintion in (c).)e) (Bonus) Show that if H and K are perpendicular, then R H (K) =K, where R Hdenotes the reflection in H.6

⎡4. Let A = 1 ⎣ 2 −1 2⎤32 2 −1 ⎦.−1 2 2a) Show that g defined by g(v) =Av is an orientation-preserving isometry of S 2 .b) Explain why g is a rotation about a = √ 33 (1, 1, 1) ∈ S2 .c) Find θ ∈ [−π, π) such that g is rotation by the angle θ about the point a ∈ S 2 in (b).Be sure you get the sign of θ correct. (You do not need to check your answer usingthe formula R a,θ (v) =(v · a)(1 − cos θ)a + (cos θ)v + (sin θ)(a × v).)d) Explain how you would, had you the time, express g as a product of reflections ingreat circles.e) (Bonus) Express g as a product of reflections in great circles.8

5. The latitude and longitude of Ottawa, and Perth (Australia) are given below:Latitude LongitudeOttawa 45 ◦ 52 ′ N 75 ◦ 22 ′ WPerth 31 ◦ 57 ′ S 115 ◦ 52 ′ ENote that Perth is in the southern hemisphere.a) Find the (θ, ϕ) coordinates of Ottawa and Perth from the given data. Express youranswer in degrees and minutes, correct to the nearest minute.b) Let N, Ott and P respectively denote the North pole, Ottawa and Perth and considerthe spherical triangle ∆N Ott P . Find the vertex angle ˆN in degrees and minutes,correct to the nearest minute. (Draw yourself a picture looking down from the northpole and remember that 0 ≤ ˆN ≤ 180 ◦ .)c) Assuming that that the earth is a sphere of radius 6380 km, find the shortest distancefrom Ottawa to Perth. Express your answer in kilometres, correct to 3 significantfigures, i.e., in the form n 1 .n 2 n 3 × 10 k where n 1 ,n 2 ,n 3 and k are integers, 9 ≥ n 1 > 0and 9 ≥ n 2 ,n 3 ≥ 0.d) (Bonus) If you were to fly from Ottawa to Perth along the arc of the great circle Ott P,find your heading as you arrive in Perth. Express the angle part of your answer indegrees and minutes, correct to the nearest minute.10

6. Let N =(0, 0, 1) andf : S 2 −{N} −→ H = {(x, y, 0) | x, y ∈ R}be the stereographic projection, and let ϕ, θ denote the spherical polar coordinates on S 2 .a) Describe geometrically how f is defined. (Do not give an algebraic formula for f.)b) Let α ∈ (0, π 2 ) and C α = {P ∈ S 2 | ϕ(P )=α} be the circle on S 2 which is aline of latitude in the northern hemispshere. By computing the length of the segmentOf(P ), show that f(C α ) is a circle in H, centred on O =(0, 0, 0), with radiussin α1−cos α .(Hint: You do not need to use an algebraic formula for f: look along a line in H thatis perpendicular to the segment Of(P ) and discover some similar triangles.)c) Now suppose C is any great circle on S 2 containing N. Describe the image of C −{N}under the stereographic projection, giving all details, using a geometric argument.(Do not use an algebraic formula for f.)d) Which (if any) of the following are true for f? (No justification is necessary.)i) It is an isometry.ii) It preserves area.iii) It preserves angles.iv) It preserves the shape of geodesics.12

This page is intentionally (almost) blank.13

This page is also intentionally (almost) blank.14