Recapitulation - Σχολή Μηχανολόγων Μηχανικών Ε.Μ.Π.

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και ΚατασκευώνΜΗΧΑΝΙΣΜΟΙ&ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ∆ΙΑΣΜΟ ΜΗΧΑΝΩΝ- 19.1 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και ΚατασκευώνCopyright © ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευών - 2012.Με επιφύλαξη παντός δικαιώµατος. All rights reserved.Απαγορεύεται η χρήση, αντιγραφή, αποθήκευση και διανοµή της παρούσης εργασίας, εξ ολοκλήρου ή τµήµατοςαυτής, για πάσης φύσεως εµπορικό ή επαγγελµατικό σκοπό. Επιτρέπεται η ανατύπωση, αποθήκευση και διανοµήγια σκοπό µη κερδοσκοπικό, εκπαιδευτικής ή ερευνητικής φύσεως, υπό την προϋπόθεση να αναφέρεται η πηγήπροέλευσης και να διατηρείται το παρόν µήνυµα.- 19.2 -

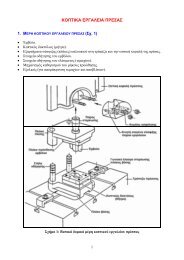
Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευών- Σε µία σύνδεση ανωτέρας τάξεως δεν προσµετρούµε ως µέλος εκείνο το στοιχείο πουπαρεµβάλλεται µεταξύ των συνεργαζοµένων καµπυλών (επιφανειών). Μία τέτοια τυπικήπερίπτωση αποτελεί ένας τροχός, προσαρµοσµένος στο άκρο ενός µέλους και δυνάµενοςνα κινηθεί επί επίπεδης επιφάνειας. Είτε ο τροχός περιστρέφεται γύρω από τον άξονά τουείτε ο τροχός είναι ‘µπλοκαρισµένος’, η κινηµατική κατάσταση του µηχανισµού στονοποίο ανήκει ο τροχός δεν µεταβάλλεται. Γι’ αυτό και δεν προσµετρούµε τον τροχό ωςµέλος, ούτε και τη δυνατότητα περιστροφής του γύρω από τον άξονά του ως ΒαθµόΕλευθερίας του µηχανισµού.ΠαράδειγµαΓια την απεικονιζόµενη διάταξη:Α) Να αναγνωρισθούν τα είδη κινηµατικής σύζευξης σε κάθε µία από τις θέσεις σύνδεσης.Β) Να υπολογισθεί (αναλυτικά και αιτιολογηµένα) το πλήθος των βαθµών ελευθερίας.Γ) Να βρεθεί εάν πρόκειται για υπερστατική κατασκευή ή στερεό σώµα ή µηχανισµό.Σχήµα 1: Εξεταζόµενη διάταξηΟι θέσεις σύνδεσης είναι οι: Α, B, C, D.Θέση A: περιστροφική άρθρωση µεταξύ µέλους (ΑΒ) και βάσηςΘέση Β: περιστροφική άρθρωση µεταξύ µέλους (ΑΒ) και (ΒD) KAIπεριστροφική άρθρωση µεταξύ µέλους (ΑΒ) και (ΒC)(∆ΙΠΛΗ άρθρωση)Θέση C: σύνδεση ανωτέρας τάξεως µεταξύ µέλους (BC) και βάσηςΘέση D: περιστροφική άρθρωση µεταξύ µέλους (ΒD) και εµβόλου D KAIπρισµατική άρθρωση µεταξύ εµβόλου (D) και βάσης(∆ΙΠΛΗ άρθρωση)Για τον τύπο του Kutzbach:n = 3 µέλη (ΑΒ, BC, BD) + 1 βάση + 1 έµβολο = 5Πλήθος συνδέσεων µε (1-ΒΕ): A,B,B,D,D, άρα f =5 1Πλήθος συνδέσεων µε (2-ΒΕ) (ανωτέρας τάξεως): C, άρα f2=1Με αντικατάσταση στον τύπο του Kutzbach, προκύπτει:F = 3 n −1 − 2 f − f = 3 5 −1 − 2× 5 − 1× 1 = 12 −10 − 1 = 1( ) ( )1 2Άρα, η εξεταζόµενο διάταξη διαθέτει F=1 Βαθµό Ελευθερίας.Επειδή F>0, η εξεταζόµενη διάταξη είναι µηχανισµός.Παρατήρηση:Εάν προέκυπτε F=0, τότε η εξεταζόµενη διάταξη θα ήταν στερεό και ισοστατικό σώµα.Εάν προέκυπτε F

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και ΚατασκευώνΑναπαράσταση θέσεως µε τη χρήση του οµογενούς µετασχηµατισµούΈστω το αδρανειακό σύστηµα αναφοράς ΣΣ{ I } και το τοπικό σύστηµα αναφοράς ΣΣ{ B }, τοοποίο προκύπτει από µία µεταφορά του ΣΣ{ I } και από µία στροφή του ΣΣ{ I }. Επίσης, έστωσηµείο ενδιαφέροντος P , µε γνωστό διάνυσµα θέσης r Bως προς το ΣΣ{ B }, και έστω ότιαναζητούµε την γραφή του διανύσµατος θέσης του σηµείου P ως προς το ΣΣ{ I }. Ισχύει: r = H rόπου ο τελεστής H I , B είναι ο πίνακας του οµογενούς µετασχηµατισµού.Στις 2∆, το διάνυσµα θέσης r Bενός σηµείου P ως προς το ΣΣ{ B } είναι:II , B ⎡ xB⎤rB= ⎢y ⎥⎣ B ⎦και ο πίνακας του οµογενούς µετασχηµατισµού είναι:HI , B⎡cosϑ−sinϑxo⎤=⎢sinϑcosϑy⎥⎢ o ⎥⎢⎣0 0 1 ⎥⎦Ο τετραγωνικός υποπίνακας από H I , B ( 1,1)έως και I , B ( 2, 2)ο υποπίνακας-στήλη από H ( ) έως και ( )BH είναι το µητρώο στροφής, ενώI , B 1,3 H I , B 2,3 είναι το διάνυσµα θέσης r o.Στις 3∆, ο πίνακας του οµογενή µετασχηµατισµού προκύπτει ίσος µε:⎡nx ox ax xo⎤⎢ny oy ay y⎥oH I , B = ⎢⎥⎢ nz oz az zo⎥⎢⎥⎣ 0 0 0 1 ⎦Ο τετραγωνικός υποπίνακας από H ( ) έως και ( )I B, 1,1⎡nx ox ax⎤R =⎢ny oy a⎥⎢ y ⎥⎢⎣nz oz a ⎥z ⎦ενώ ο υποπίνακας-στήλη από H ( ) έως και ( )I B, 1, 4Υπάρχουν τρεις ειδικές περιπτώσεις στροφής:• Στροφή περί του x − άξονα• Στροφή περί του y − άξονα⎡1 0 0 ⎤RI , B=⎢0 cosϑ sinϑ⎥⎢−⎥⎢⎣0 sinϑcosϑ⎥⎦RI , B⎡ cosϑ0 sinϑ⎤=⎢0 1 0⎥⎢ ⎥⎢⎣−sinϑ0 cosϑ⎥⎦H I , B 3,3 είναι το µητρώο στροφής:H I , B 3, 4 είναι το διάνυσµα θέσης r o.- 19.5 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευών• Στροφή περί του z − άξονα⎡cosϑ−sinϑ0⎤RI , B=⎢sinϑcosϑ0⎥⎢ ⎥⎢⎣0 0 1⎥⎦Σχετικά µε την σύνθεση οµογενών αναπαραστάσεων, ισχύει:HI , v= HI ,1H1,2 H2,3...Hv−2, v−1Hv−1,vόπου ΣΣ{ I } είναι το αδρανειακό σύστηµα αναφοράς και ΣΣ{ 1 } , ΣΣ{ 2 }, …, ΣΣ{ v } είναιτοπικά συστήµατα αναφοράς, ενώ ο οµογενής µετασχηµατισµός H I ,1 , περιγράφει τηµετάβαση από το ΣΣ{ I } στο ΣΣ{ 1 } , ο οµογενής µετασχηµατισµός H 1,2 , περιγράφει τηµετάβαση από το ΣΣ{ 1 } στο ΣΣ{ 2 } και εν γένει ο οµογενής µετασχηµατισµός H ( ν −1 ),νπεριγράφει τη µετάβαση από το ΣΣ{ v − 1}στο ΣΣ{ v } .Εξίσωση θέσεως αρθρωτού µηχανισµούΜε κατάλληλη χρήση του οµογενούς µετασχηµατισµού, είναι δυνατή η κατάστρωση τηςεξίσωσης θέσεως ενός αρθρωτού µηχανισµού. Τυπικά παραδείγµατα είναι οι κλειστέςκινηµατικές αλυσίδες µε 3 µέλη και µε 4 µέλη.(α)(β)Σχήµα 2: (α) Κλειστή κινηµατική αλυσίδα (ABCA) µε 3 µέλη και (β) κλειστή κινηµατικήαλυσίδα (ABCDA) µε 4 µέληΟι εξισώσεις θέσεως της κλειστής κινηµατικής αλυσίδας µε 3 µέλη (βλ. Σχήµα 2α) είναι:AC = AB cosϑ+ BC cosϑ( ) ( ) ( )( AB) sinϑ= ( BC)sin1 3ϑ1 3Οι εξισώσεις θέσεως της κλειστής κινηµατικής αλυσίδας µε 4 µέλη (βλ. Σχήµα 2β) είναι:l = l cos ϑ + ϑ + ϑ + l cos ϑ + ϑ + l cos ϑ( ) ( ) ( )( ϑ ϑ ϑ ) ( ϑ ϑ ) ( ϑ )4 3 1 2 3 2 1 2 1 10 = l sin + + + l sin + + l sin3 1 2 3 2 1 2 1 1Αναλυτικός (αλγεβρικός) υπολογισµός ταχύτηταςΠροκύπτει από τη χρονική παραγώγιση των εξισώσεων θέσεως του µηχανισµού.Αναλυτικός (αλγεβρικός) υπολογισµός επιτάχυνσηςΠροκύπτει από τη χρονική παραγώγιση των εξισώσεων ταχύτητας του µηχανισµού.- 19.6 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευών∆ιανυσµατικός υπολογισµός ταχύτηταςΈστω µηχανισµός και έστω αδρανειακό σύστηµα αναφοράς I , το οποίο επιλέγουµεαυθαίρετα. Έστω σηµείο Ρ του µηχανισµού και έστω τοπικό σύστηµα αναφοράς loc , τοοποίο, επίσης, επιλέγουµε αυθαίρετα. Σε έναν αρθρωτό µηχανισµό, είναι συνήθης πρακτική οορισµός ενός τοπικού συστήµατος συντεταγµένων σε κάθε µέλος του µηχανισµού. Ηταχύτητα του σηµείου P υπολογίζεται διανυσµατικά από την εξίσωση:υP, I= υloc, I+ υP, loc+ ω ⊗ rP , loc̃ ̃ ̃ ̃ ̃όπου: είναι η ταχύτητα του σηµείου Ρ ως προς το αδρανειακό σύστηµα αναφοράς IP,Iυ̃υ̃loc , I: είναι η γραµµική ταχύτητα του τοπικού συστήµατος αναφοράς loc ως προς τοαδρανειακό σύστηµα αναφοράς I (λόγω µεταφοράς του τοπικού συστήµατοςαναφοράς loc ως προς το αδρανειακό σύστηµα αναφοράς I )P,locυ̃ω̃ :r̃P , loc: είναι η γραµµική ταχύτητα του σηµείου Ρ ως προς το τοπικό σύστηµα αναφοράς loc(λόγω µετακίνησης του Ρ ως προς το τοπικό σύστηµα αναφοράς loc )είναι η γωνιακή ταχύτητα του σηµείου Ρ ως προς το τοπικό σύστηµα αναφοράς loc(λόγω περιστροφής του Ρ ως προς το τοπικό σύστηµα αναφοράς loc ): είναι το διάνυσµα θέσεως του σηµείου Ρ ως προς το τοπικό σύστηµα αναφοράς locr P ,: εφαπτοµενική συνιστώσα ταχύτητας̃ locω ⊗ ̃Παρατήρηση: Εάν το σηµείο ενδιαφέροντος Ρ ανήκει σε µέλος, το µήκος του οποίου δενµεταβάλλεται κατά τη διάρκεια της λειτουργίας του µηχανισµού, τότε ισχύει υP, loc= 0 . Σε̃ ̃αντίθετη περίπτωση, ισχύει υP, loc≠ 0 . Τυπικές περιπτώσεις δυνατότητας (όχι υποχρεωτικά)̃ ̃µεταβολής µήκους ενός µέλους µηχανισµού είναι ο τηλεσκοπικός βραχίονας και τοσυρµατόσχοινο ανάρτησης βάρους σε έναν γερανό (π.χ. κατά την ανύψωση βάρους).∆ιανυσµατικός υπολογισµός επιτάχυνσηςΓια το προαναφερθέν σηµείο Ρ, η επιτάχυνση υπολογίζεται διανυσµατικά από την εξίσωση:( r )aP, I= aloc, I+ aP, loc+ 2ω ⊗ υP, loc+ ̇ ω ⊗ rP , loc+ ω ⊗ ω ⊗P,loc̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃όπου: είναι η επιτάχυνση του σηµείου Ρ ως προς το αδρανειακό σύστηµα αναφοράς IP,Iããloc , I: είναι η γραµµική επιτάχυνση του τοπικού συστήµατος αναφοράς loc ως προς τοαδρανειακό σύστηµα αναφοράς I (λόγω µεταφοράς του τοπικού συστήµατοςαναφοράς loc ως προς το αδρανειακό σύστηµα αναφοράς I )P,locã: είναι η γραµµική επιτάχυνση του σηµείου Ρ ως προς το τοπικό σύστηµα αναφοράς(λόγω µετακίνησης του Ρ ως προς το τοπικό σύστηµα αναφοράς loc )2ω ⊗υ̃P,loc: είναι η επιτάχυνση Coriolis̃̇ ω ⊗ r ̃ P , loc: είναι η εφαπτοµενική συνιστώσα της επιτάχυνσης̃ω ⊗ ( ω ⊗ r , ) : είναι η κάθετη συνιστώσα της επιτάχυνσης (κεντροµόλος)̃ ̃ ̃ P loc: είναι η γωνιακή ταχύτητα του σηµείου Ρ ως προς το τοπικό σύστηµα αναφοράς locω̃(λόγω περιστροφής του Ρ ως προς το τοπικό σύστηµα αναφοράς loc )- 19.7 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευώνr̃P , loc: είναι το διάνυσµα θέσεως του σηµείου Ρ ως προς το τοπικό σύστηµα αναφοράς locΠαρατήρηση: Εάν το σηµείο ενδιαφέροντος Ρ ανήκει σε µέλος, το µήκος του οποίου δενµεταβάλλεται κατά τη διάρκεια της λειτουργίας του µηχανισµού, τότε ισχύει υP, loc= 0 , άρα̃ ̃µηδενίζεται και η επιτάχυνση Coriolis. Σε αντίθετη περίπτωση, ισχύει υP, loc≠ 0 και υπάρχει̃ ̃συνεισφορά από την επιτάχυνση Coriolis.Παράδειγµα: Μηχανισµός Στροφάλου - ∆ιωστήρα – ΕµβόλουΓια τον µηχανισµό Στροφάλου - ∆ιωστήρα – Εµβόλου (βλ. Σχήµα 3) στο xy-επίπεδο, ναβρεθούν:(Α) οι εξισώσεις θέσεως,(Β) οι εξισώσεις ταχύτητας (πρώτα αναλυτικά (αλγεβρικά) και κατόπιν διανυσµατικά),(Γ) οι εξισώσεις επιτάχυνσης (πρώτα αναλυτικά (αλγεβρικά) και κατόπιν διανυσµατικά) καινα αναγνωρισθούν οι επί µέρους όροι (π.χ. Coriolis, εφαπτοµενική, κοκ).Επίσης:(∆) να κατασκευασθούν τα διαγράµµατα ταχύτητας και επιτάχυνσης για το µέλος (ΑΒ).∆ίδονται: (AB), (BC): σταθερά µήκη, είσοδος: γωνία θ, έξοδος: γωνία φΣχήµα 3: Μηχανισµός Στροφάλου - ∆ιωστήρα – Εµβόλου στο xy-επίπεδο (απεικονίζεται καιτο αδρανειακό σύστηµα αναφοράς x Ι O Ι y Ι )Υπολογισµός εξισώσεων θέσεωςΟ µηχανισµός Στροφάλου - ∆ιωστήρα – Εµβόλου προκύπτει από την κλειστή κινηµατικήαλυσίδα µε 3 µέλη (βλ. Σχήµα 2α), εάν το τµήµα (AC) αφαιρεθεί και θεωρηθεί ως µεταβλητήαπόσταση u (βλ. Σχήµα 3). Συνεπώς, οι εξισώσεις θέσεως του εξεταζοµένου µηχανισµούπροκύπτουν µε κατάλληλη προσαρµογή των εξισώσεων θέσεως της κλειστής κινηµατικήςαλυσίδας µε 3 µέλη. Ειδικότερα, ισχύει:Οι εξισώσεις θέσεως της κλειστής κινηµατικής αλυσίδας µε 3 µέλη (βλ. Σχήµα 2α) είναι:( AC ) = ( AB) cosϑ1 + ( BC)cosϑ3(Ε1)AB sinϑ= BC sinϑ( ) ( )1 3Αντικαταστάσεις: (AB)->r, (BC) -> l, (AC)->u, θ 1 ->θ, θ 3 ->φΤελικά, οι ζητούµενες εξισώσεις θέσεως προκύπτουν ίσες µε:u = r cosθ+ l cosϕr sinθ= l sinϕΥπολογισµός εξισώσεων ταχύτητας (αλγεβρικά)(Ε2)- 19.8 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και ΚατασκευώνΠροκύπτουν µε χρονική παραγώγιση των εξισώσεων (Ε1):u̇= −r ̇ θ sinϑ − l ̇ ϕ sinϕr ̇ θ cosθ = l ̇ ϕ cosϕ(Ε3)Παρατήρηση: τα µήκη (AB), (BC) είναι σταθερά, άρα δεν συµµετέχουν στην παραγώγιση.Υπολογισµός εξισώσεων επιτάχυνσης (αλγεβρικά)Προκύπτουν µε χρονική παραγώγιση των εξισώσεων (Ε3):2 2u̇̇= −r ̇̇ θ sinϑ − r ̇ θ cosϑ − l ̇̇ ϕ sinϕ − l ̇ ϕ cosϕ2 2r ̇̇ θ cosϑ − r ̇ θ sinϑ − l ̇̇ ϕ cosϕ + l ̇ ϕ sinϕ= 0(Ε4)Υπολογισµός εξισώσεων ταχύτητας (διανυσµατικά)Για το σηµείο Β:Ορίζουµε τοπικό σύστηµα x 1 O 1 y 1 , (σύστηµα {loc}) παράλληλο ως προς το αδρανειακόσύστηµα αναφοράς και µε αρχή αξόνων στη θέση Α (βλ. Σχήµα 4).Σχήµα 4: Ορισµός τοπικού συστήµατος x 1 O 1 y 1Η ταχύτητα στο σηµείο Β, ως προς το αδρανειακό σύστηµα αναφοράς, ισούται µε:υB, I= υloc, I+ υB, loc+ ω ⊗ rB , loc(Ε5)̃ ̃ ̃ ̃ ̃όπουυloc, I= 0 (διότι η αρχή αξόνων του τοπικού συστήµατος συµπίπτει µε το ακλόνητο̃σηµείο Α)υB, loc= 0 (διότι η απόσταση του σηµείου Β από το σηµείο Α είναι σταθερή κατά τη̃λειτουργία του µηχανισµού, δηλαδή το σηµείο Β ούτε προσεγγίζει ούτεαποµακρύνεται από το σηµείο Α)ω = ⎡0 0 ̇ ⎣ θ ⎤̃⎦T[ θ θ ]διότι το σηµείο Β περιστρέφεται γύρω από το Α µε γωνιακή ταχύτηταθ̇ , άξονα περιστροφής κάθετο στο επίπεδο του χαρτιού (z-άξονας) καιφορά ανθωρολογιακήr,cos sin 0 TB loc= r r διάνυσµα θέσεως του σηµείου Β ως προς το τοπικό σύστηµα̃x 1 O 1 y 1 i j kω ⊗ rB , loc= 0 0 ̇ θ = i ( 0 − r ̇ θ sinθ ) − j ( 0 − r ̇ θ cosθ) + k ( 0 − 0)⇒̃ ̃r cosθr sinθ0- 19.9 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευών⎡−ṙ θ sinθ⎤⎢ ⎥⇒ ω ⊗ rB , loc= r ̇ ⎢ θ cosθ̃ ̃⎥⎢ 0 ⎥⎣ ⎦Αντικαθιστώντας όλα τα ανωτέρω στην εξίσωση (Ε5), προκύπτει:⎡−ṙ θ sinθ ⎤ ⎡−ṙ θ sinθ⎤⎢ ⎥ ⎢ ⎥υB, I= 0 + 0 + r ̇ θ cosθ ⇒ υB,I= r ̇⎢ ⎥ ⎢ θ cosθ̃̃⎥⎢ 0 ⎥ ⎢ 0 ⎥⎣ ⎦ ⎣ ⎦(Ε6)(Ε7)Για το σηµείο C:Επαναλαµβάνουµε την ίδια διαδικασία, όπως και για το σηµείο Β. Ορίζουµε τοπικό σύστηµαx 2 O 2 y 2 , (σύστηµα {loc}) παράλληλο ως προς το αδρανειακό σύστηµα αναφοράς και µε αρχήαξόνων στη θέση Β (βλ. Σχήµα 5).Σχήµα 5: Ορισµός τοπικού συστήµατος x 2 O 2 y 2Η ταχύτητα στο σηµείο C, ως προς το αδρανειακό σύστηµα αναφοράς, ισούται µε:υC, I= υloc, I+ υC, loc+ ω ⊗ rC , loc(Ε8)̃ ̃ ̃ ̃ ̃όπουυloc, I= υA,I(διότι η αρχή αξόνων του τοπικού συστήµατος x 2 O 2 y 2 συµπίπτει µε το σηµείο̃ ̃Β, η ταχύτητα του οποίου υπολογίσθηκε στην προηγούµενη ενότητα)υC, loc= 0 (διότι η απόσταση του σηµείου C από το σηµείο B είναι σταθερή κατά τη̃λειτουργία του µηχανισµού, δηλαδή το σηµείο C ούτε προσεγγίζει ούτεαποµακρύνεται από το σηµείο B)[ 0 0 ϕ]ω = − ̇̃T[ ϕ ϕ ]διότι το σηµείο C περιστρέφεται γύρω από το B µε γωνιακή ταχύτηταϕ̇ , άξονα περιστροφής κάθετο στο επίπεδο του χαρτιού (z-άξονας) καιφορά ωρολογιακήr,cos sin 0 Tc loc= l −lδιάνυσµα θέσεως του σηµείου C ως προς το τοπικό σύστηµα̃x 2 O 2 y 2 i j kω ⊗ rC , loc= 0 0 − ̇ ϕ = i ( 0 − l ̇ ϕ sinϕ ) − j ( 0 + l ̇ ϕ cosϕ) + k ( 0 − 0)⇒̃ ̃l cosϕ−lsinϕ0⎡−l̇ ϕ sinϕ⎤⇒ ω ⊗ rC , loc=⎢−l̇ ϕ cosϕ⎥̃ ̃ ⎢ ⎥⎢⎣0 ⎥⎦(Ε9)- 19.10 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και ΚατασκευώνΑντικαθιστώντας όλα τα ανωτέρω στην εξίσωση (Ε8), προκύπτει:⎡−r ̇ θ sinθ ⎤ ⎡−l ̇ ϕ sinϕ ⎤ ⎡−r ̇ θ sinθ − l ̇ ϕ sinϕ⎤⎢ ⎥ ⎢ ⎥υC, I= 0 + r ̇ θ cosθ ⎢lϕ cosϕ ⎥⎢ ⎥ + − ̇ ⇒ υC,I= r ̇⎢ ⎥ ⎢ θ cosθ − l ̇ ϕ cosϕ⎥ (Ε10)̃̃⎢ 0 ⎥ ⎢⎣0 ⎥⎦⎢ 0 ⎥⎣ ⎦ ⎣ ⎦Από το Σχήµα 3, προκύπτει ότι:- η οριζόντια συνιστώσα της ταχύτητας στο σηµείο C ισούται µε u̇- η κατακόρυφη συνιστώσα της ταχύτητας στο σηµείο C είναι µηδενική, διότι στο σηµείοC η υπάρχουσα πρισµατική άρθρωση εµποδίζει κατακόρυφες µετακινήσειςΜε βάση αυτές τις παρατηρήσεις, η εξίσωση (Ε10) γράφεται και ως εξής:⎡−ṙ θ sinθ ⎤ ⎡−l̇ ϕ sinϕ⎤⎢ ⎥ u rθ sinθ lϕ sinϕυC,I0 rθ cosθ ⎢lϕ cosϕ⎥ ⎡ ⎤ ⎡−̇ − ⎤= + ̇̇⎢ ⎥ + − ̇⎢ ⎥⇒ ⎢ = ⎢ ⎥0⎥(Ε11)̃⎢rθ cosθ − lϕ cosϕ0 ⎥ ⎢ 0 ⎥⎣ ⎦̇⎣ ̇ ⎦⎣ ⎦ ⎣ ⎦Παρατήρηση: Οι εξισώσεις (Ε3) και (Ε11) ταυτίζονται, ως αναµενόταν.Υπολογισµός εξισώσεων επιτάχυνσης (διανυσµατικά)Για το σηµείο Β:Με βάση το ήδη ορισθέν τοπικό σύστηµα x 1 O 1 y 1 , η επιτάχυνση στο σηµείο Β, ως προς τοαδρανειακό σύστηµα αναφοράς, ισούται µε:( r )aB, I= aloc, I+ aB, loc+ 2ω ⊗ υB, loc+ ̇ ω ⊗ rB , loc+ ω ⊗ ω ⊗B,loc(Ε12)̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃όπουaloc, I= 0 (διότι η αρχή αξόνων του τοπικού συστήµατος συµπίπτει µε το ακλόνητο̃ ̃σηµείο Α)aB, loc= 0 (διότι η απόσταση του σηµείου Β από το σηµείο Α είναι σταθερή κατά τη̃ ̃λειτουργία του µηχανισµού)2ω ⊗ υ B , loc= 0 η επιτάχυνση Coriolis είναι µηδενική διότι υB, loc= 0 (βλ. ενότητα για̃ ̃ ̃̃ταχύτητα στο σηµείο Β)[ θ θ ]r,cos sin 0 TB loc= r r διάνυσµα θέσεως του σηµείου Β ως προς το τοπικό σύστηµα̃x 1 O 1 y 1Tω = ⎡0 0 ̇ ⎣ θ ⎤̃⎦(βλ. ενότητα για ταχύτητα στο σηµείο Β)̇ ω ⊗ r ̃ B , loc: είναι η εφαπτοµενική συνιστώσα της επιτάχυνσης̃ i j k̇ ω ⊗ rB , loc= 0 0 ̇̇ θ = i ( 0 − r ̇̇ θ sinθ ) − j ( 0 − r ̇̇ θ cosθ) + k ( 0 − 0)⇒̃ ̃r cosθr sinθ0ω ⊗̃( ω r , ) B loc̃⊗ ̃̇̃⎡−ṙ̇ θ sinθ⎤⎢ ̇̇ ⎥⇒ ω ⊗ rB , loc= ⎢ rθ cosθ⎥̃⎢⎣: είναι η κάθετη συνιστώσα της επιτάχυνσης (κεντροµόλος)0⎥⎦(Ε13)- 19.11 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευών ⎡−r ̇ θ sinθ⎤ i j k⎢ ⎥ω ⊗( ω ⊗ rB , loc ) = ω ⊗ r ̇ θ cosθ = 0 0 ̇ θ ⇒̃ ̃ ̃ ̃⎢ ⎥⎢ 0 ⎥⎣ ⎦−ṙ θ sinθ r ̇ θ cosθ02 2⇒ ω ⊗( ω ⊗ rB , loc ) = i ( 0 − r ̇ θ cosθ ) − j ( 0 + r ̇ θ sinθ) + k ( 0 − 0)⇒̃ ̃ ̃2⎡−ṙ θ cosθ⎤⎢ 2 ⎥⇒ ω ⊗( ω ⊗ rB , loc ) = −ṙ ⎢ θ sinθ̃ ̃ ̃⎥⎢ 0 ⎥⎣ ⎦Αντικαθιστώντας όλα τα ανωτέρω στην εξίσωση (Ε12), προκύπτει:2 2⎡−r ̇̇ θ sinθ ⎤ ⎡−r ̇ θ cosθ ⎤ ⎡−r ̇̇ θ sinθ − r ̇ θ cosθ⎤⎢ ⎥ ⎢ 2 ⎥ ⎢ 2 ⎥aB, I= 0 + 0 + 0 + r ̇̇ θ cosθ + −r ̇ θ sinθ ⇒ aB,I= r ̇̇⎢ ⎥ ⎢ ⎥ ⎢ θ cosθ − r ̇ θ sinθ̃ ̃ ̃ ̃ ̃⎥⎢ 0 ⎥ ⎢ 0 ⎥ ⎢ 0 ⎥⎣ ⎦ ⎣ ⎦ ⎣ ⎦(Ε14)(Ε15)Για το σηµείο Γ:Επαναλαµβάνουµε την ίδια διαδικασία, όπως και για το σηµείο Β. Με βάση το ήδη ορισθέντοπικό σύστηµα x 2 O 2 y 2 , η επιτάχυνση στο σηµείο C, ως προς το αδρανειακό σύστηµααναφοράς, ισούται µε:( r )aC , I= aloc, I+ aC , loc+ 2ω ⊗ υC, loc+ ̇ ω ⊗ rC , loc+ ω ⊗ ω ⊗C,loc(Ε16)̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃όπουaloc, I= aB,I(διότι η αρχή αξόνων του τοπικού συστήµατος x 2 O 2 y 2 συµπίπτει µε το σηµείο̃ ̃Β, η επιτάχυνση του οποίου υπολογίσθηκε στην προηγούµενη ενότητα)aC, loc= 0 (διότι η απόσταση του σηµείου C από το σηµείο B είναι σταθερή κατά τη̃ ̃λειτουργία του µηχανισµού)2ω ⊗ υ C , loc= 0 η επιτάχυνση Coriolis είναι µηδενική διότι υC, loc= 0 (βλ. ενότητα για̃ ̃ ̃̃ταχύτητα στο σηµείο C)[ ϕ ϕ ]r,cos sin 0 Tc loc= l −lδιάνυσµα θέσεως του σηµείου C ως προς το τοπικό σύστηµα̃x 2 O 2 y 2Tω = [ 0 0 − ̇ ϕ](βλ. ενότητα για ταχύτητα στο σηµείο C)̃̇ ω ⊗ r ̃ C , loc: είναι η εφαπτοµενική συνιστώσα της επιτάχυνσης̃ i j k̇ ω ⊗ rC , loc= 0 0 − ̇̇ ϕ = i ( 0 − l ̇̇ ϕ sinϕ ) − j ( 0 + l ̇̇ ϕ cosϕ) + k ( 0 − 0)⇒̃ ̃l cosϕ−lsinϕ0ω ⊗̃( ω r , ) C loc⊗̃ ̃⎡−l̇̇ ϕ sinϕ⎤⇒ ̇ ω ⊗ rC , loc=⎢−l̇̇ ϕ cosϕ⎥̃ ̃ ⎢ ⎥⎢⎣0 ⎥⎦: είναι η κάθετη συνιστώσα της επιτάχυνσης (κεντροµόλος)(Ε17)- 19.12 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευών ⎡−l ̇ ϕ sinϕ⎤ i j kω ⊗ ( ω ⊗ rc , loc ) = ω ⊗⎢− l ̇ ϕ cosϕ ⎥= 0 0 − ̇ ϕ ⇒̃ ̃ ̃ ̃ ⎢ ⎥⎣⎢ 0 ⎦⎥ −l̇ ϕ sinϕ −l̇ ϕ cosϕ02 2⇒ ω ⊗ ( ω ⊗ rC , loc ) = i ( 0 − l ̇ ϕ cosϕ ) − j ( 0 − l ̇ ϕ sinϕ) + k ( 0 − 0)⇒̃ ̃ ̃2⎡−l̇ ϕ cosϕ⎤⎢ 2 ⎥⇒ ω ⊗ ( ω ⊗ rB , loc ) = ⎢ l ̇ ϕ sinϕ⎥(Ε18)̃ ̃ ̃⎢ 0 ⎥⎣ ⎦Αντικαθιστώντας όλα τα ανωτέρω στην εξίσωση (Ε16), προκύπτει:2 2⎡−r ̇̇ θ sinθ − r ̇ θ cosθ ⎤ ⎡−l ̇̇ ϕ sinϕ ⎤ ⎡−l̇ ϕ cosϕ⎤⎢ 2 ⎥ ⎢ 2 ⎥aC , I= r ̇̇ θ cosθ − r ̇ θ sinθ 0 0⎢lϕ cosϕ ⎥⎢ ⎥ + + + − ̇̇ + ⎢ l ̇⎢ ⎥ϕ sinϕ⎥ ⇒̃ ̃ ̃⎢ 0 ⎥ ⎢⎣ 0 ⎥⎦ ⎢ 0 ⎥⎣⎦⎣ ⎦2 2⎡−r ̇̇ θ sinθ − r ̇ θ cosθ − l ̇̇ ϕ sinϕ − l ̇ ϕ cosϕ⎤⎢2 2 ⎥⇒ aC , I= r ̇̇ θ cosθ − r ̇⎢ θ sinθ − l ̇̇ ϕ cosϕ + l ̇ ϕ sinϕ⎥(Ε19)̃⎢0⎥⎣⎦Σε συνέχεια των παρατηρήσεων επί του Σχήµατος 3, προκύπτει ότι:- η οριζόντια συνιστώσα της επιτάχυνσης στο σηµείο C ισούται µε u̇̇- η κατακόρυφη συνιστώσα της επιτάχυνσης στο σηµείο C είναι µηδενική, διότι στοσηµείο C η υπάρχουσα πρισµατική άρθρωση εµποδίζει κατακόρυφες µετακινήσειςΜε βάση αυτές τις παρατηρήσεις, η εξίσωση (Ε19) γράφεται και ως εξής:2 2⎡u̇̇ ⎤ ⎡−r ̇̇ θ sinθ − r ̇ θ cosθ − l ̇̇ ϕ sinϕ − l ̇ ϕ cosϕ⎤⎢ 2 20⎥ = ⎢⎥(Ε20)⎣ ⎦ r ̇̇ θ cosθ − r ̇⎣ θ sinθ − l ̇̇ ϕ cosϕ + l ̇ ϕ sinϕ⎦Παρατήρηση: Οι εξισώσεις (Ε4) και (Ε20) ταυτίζονται, ως αναµενόταν.∆ιάγραµµα ταχύτητας και επιτάχυνσης για το µέλος (ΑΒ)Το σηµείο Α είναι ακλόνητο, άρα διαθέτει µηδενική ταχύτητα και επιτάχυνση.Από τον υπολογισµό της ταχύτητας στο σηµείο Β, προκύπτει ότι το σηµείο Β εµφανίζει µόνοεφαπτοµενική συνιστώσα ταχύτητας ίση µε⎡−ṙ θ sinθ⎤⎢ ⎥υB, I= ( υB,I ) = r ̇ θ cosθεϕαπτ ⎢ ⎥(Ε21)̃ ̃⎢ 0 ⎥⎣ ⎦Από τον υπολογισµό της επιτάχυνσης στο σηµείο Β, προκύπτει ότι το σηµείο Β εµφανίζειµόνο εφαπτοµενική συνιστώσα ταχύτητας ίση µε⎡−ṙ̇ θ sinθ⎤⎢ ⎥( aB,I ) = r ̇̇ θ cosθεϕαπτ ⎢ ⎥(Ε22)̃⎢ 0 ⎥⎣ ⎦και κάθετη (κεντροµόλο) συνιστώσα ταχύτητας ίση µε- 19.13 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευών2⎡−ṙ θ cosθ⎤⎢ 2 ⎥( aB,I ) = −ṙ θ sinθκεντροµ ⎢ ⎥(Ε23)̃⎢ 0 ⎥⎣ ⎦Βάσει αυτών των πληροφοριών, τα διαγράµµατα ταχύτητας και επιτάχυνσης είναι αυτά πουαπεικονίζονται στο Σχήµα 6.(α)(β)Σχήµα 6: ∆ιάγραµµα (α) ταχύτητας και (β) επιτάχυνσης για το µέλος (ΑΒ)Συντελεστής Αναλογίας (Mechanical Advantage)Με τη βοήθεια των µηχανισµών, είναι δυνατός ο πολλαπλασιασµός ή υπο-πολλαπλασιασµόςενός εξωτερικά ασκουµένου αιτίου (δύναµης ή ροπής). Eάν F in είναι η ‘είσοδος’ (εξωτερικάασκούµενο αίτιο) σε έναν µηχανισµό και F out είναι η ‘έξοδος’ (το, ασκούµενο από τονµηχανισµό, αποτέλεσµα), τότε ο Συντελεστής Αναλογίας (Mechanical Advantage) ορίζεταιως:⎛ F ⎞out( MA) = ⎜ ⎟(Ε24)⎝ Fin⎠Για τον υπολογισµό του λόγου (ΜΑ), είναι δυνατόν να χρησιµοποιηθεί η Αρχή ∆ιατήρησηςτης Ισχύος, η οποία ισχύει για συντηρητικά συστήµατα (δηλαδή για συστήµατα µε µηδενικέςαπώλειες). Σύµφωνα µε την εν λόγω αρχή, ισχύει:P = P(Ε25)inόπου Pinκαι Poutείναι η ισχύς ‘εισόδου’ και η ισχύς ‘εξόδου’ του µηχανισµού.Υπενθυµίζεται ότι στην περίπτωση περιστρεφόµενης κίνησης, η ισχύς ορίζεται ως:P = Mω(Ε26)όπου M είναι η αναπτυσσόµενη ροπή και ω είναι η αντίστοιχη γωνιακή ταχύτητα. Επίσης,στην περίπτωση ευθύγραµµης κίνησης, η ισχύς ορίζεται ως:P = Fiυ(Ε27)̃ ̃όπου είναι η αναπτυσσόµενη δύναµη, είναι η ταχύτητα του σηµείου εφαρµογής τηςF̃υ̃δύναµης , ενώ το σύµβολο i δηλώνει την πράξη του εσωτερικού γινοµένου.F̃Παρατήρηση: Από την εξίσωση (Ε27) προκύπτει ότι σε µία δύναµη, η οποία κινεί το σηµείοεφαρµογής της κάθετα ως προς τη διεύθυνσή της, αντιστοιχεί µηδενική ισχύς.out- 19.14 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και ΚατασκευώνΕνεργειακή Αρχή LagrangeΓια τη µελέτη ενός (οποιουδήποτε) µηχανισµού, χρειάζεται η καταγραφή των εξισώσεωνισορροπίας του. Προς τούτο, είναι δυνατόν να εφαρµόσουµε τον πρώτο νόµο του Νεύτωνα.Ωστόσο, σε πολυβάθµια δυναµικά συστήµατα, αυτή είναι µία διαδικασία αρκετά επίπονη καιδύσκολη. Αντί, λοιπόν, της Νευτώνειας προσέγγισης, προτιµούµε την ενεργειακή προσέγγισηκατά Lagrange, η οποία χαρακτηρίζεται από τρία σηµαντικά πλεονεκτήµατα:1. Αποτελεί την πλέον γενική ενεργειακή διατύπωση, στην οποία εµπλέκονται όλες οιµορφές ενέργειας και ισχύος που εµφανίζονται στα δυναµικά συστήµατα (δυναµικήενέργεια, κινητική ενέργεια, διάχυση ισχύος και εξωτερική ισχύς του συστήµατος).Συνεπώς, εφαρµόζεται σε όλες, ανεξαιρέτως, τις περιπτώσεις, όπως σε γραµµικά και µηγραµµικάµηχανικά συστήµατα, σε υδραυλικά συστήµατα, σε ηλεκτρικά συστήµατακαθώς και σε συνδυασµούς αυτών (συζευγµένα συστήµατα).2. Εµπλέκει µόνο ενεργειακές ποσότητες, οι οποίες αποτελούν βαθµωτά µεγέθη. Η συνολικήενέργεια του συστήµατος δεν είναι τίποτε άλλο παρά απλή πρόσθεση αυτών τωνβαθµωτών µεγεθών. Αντιθέτως, οι δυνάµεις, ως διανυσµατικά µεγέθη, απαιτούνδιανυσµατικές µεταξύ τους πράξεις, οι οποίες, σε ορισµένες περιπτώσεις (π.χ. εύκαµπτοςροµποτικός βραχίονας) είναι, σαφώς, πιο σύνθετες.3. Οι ενεργειακές ποσότητες σχετίζονται µε µαθηµατικές εκφράσεις τετραγωνικής µορφής,συνεπώς το τελικό ενεργειακό αποτέλεσµα δεν επηρεάζεται από τη σειρά µε την οποίααναγράφονται οι µετατοπίσεις σε µία µεταβολή. Αντιθέτως, η διαχείριση δυνάµεωναπαιτείται ιδιαίτερη προσοχή στην προσήµανσή τους.∆ιευκρινίζεται, ότι µε την Ενεργειακή Αρχή Lagrange καταλήγουµε στις εξισώσειςισορροπίας του συστήµατος, δηλαδή στις Νευτώνειες εξισώσεις ισορροπίας, µε έναν πολύαπλό και πρακτικό τρόπο.Η µαθηµατική έκφραση της Ενεργειακής Αρχής Lagrange είναι:∂ ⎛ ∂L⎞ ∂LPCPt⎜ ⎟ − + ∂ =∂∂t ⎝ ∂q̇ ⎠ ∂q ∂q̇ ∂q̇ (Ε28)Όρος αδράνειας(αντιστοιχεί σεδυνάµειςαδρανείας Fm)Όρος ελαστικότητος(αντιστοιχεί σεδυνάµεις ελατηρίουF )kΌρος διάχυσης(αντιστοιχεί σεδυνάµειςαπόσβεσης Fc)Όρος διέγερσης(αντιστοιχεί σεεξωτερικέςδυνάµεις F )όπου q είναι ανεξάρτητη κινηµατική µεταβλητή (Βαθµός Ελευθερίας) του συστήµατος, ωςPCσυµβολίζεται η ενέργεια, η οποία διαχέεται λόγω της απόσβεσης του συστήµατος, ως Ptσυµβολίζεται η ισχύς που προσφέρεται στο σύστηµα από τις εξωτερικές δυνάµεις και ως Lσυµβολίζεται η αποκαλούµενη ‘ενεργειακή µεταβλητή Lagrange’. Εξ ορισµού, ισχύει:L = T − U(Ε29)- 19.15 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευώνόπου ως T συµβολίζεται η κινητική ενέργεια του συστήµατος, η οποία συσσωρεύεται στιςµάζες του συστήµατος, ενώ ως U συµβολίζεται η δυναµική ενέργεια, η οποία συσσωρεύεταιστα ελατήρια του συστήµατος. Η εξίσωση (Ε.28) γράφεται τόσες φορές, όσες είναι οιανεξάρτητες µεταβλητές q που διαθέτει το σύστηµα. Ισοδύναµα, η εξίσωση (Ε28) γράφεταιτόσες φορές, όσοι είναι οι Βαθµοί Ελευθερίας του εξεταζοµένου συστήµατος.ΠαράδειγµαΈστω η τροχαλία του Σχήµατος 7, µαζικής ροπής αδρανείας Ι, εξωτερικής ακτίνας R,εσωτερικής ακτίνας r και αµελητέας µάζας. Ασκώντας (προς τα κάτω) µία κατακόρυφηδύναµη F, επιτυγχάνεται η κατακόρυφη ανύψωση της µάζας m, η οποία είναι ανηρτηµένηµέσω αβαρούς και µη-ελαστικού σχοινιού. Να βρεθεί η εξίσωση κίνησης της εξεταζόµενηςτροχαλίας, εφαρµόζοντας την Ενεργειακή Αρχή Lagrange και θεωρώντας αµελητέες τιςόποιες τριβές.Σχήµα 7: Εξεταζόµενη τροχαλίαΈστω ότι u είναι η µετατόπιση του σηµείου εφαρµογής της δύναµης F και έστω ότι µε hσυµβολίζεται η κατακόρυφη ανύψωση της µάζας m.Η κινητική ενέργεια του εξεταζόµενου συστήµατος (συσσωρεύεται σε στοιχεία αδρανείαςτου συστήµατος) ισούται µε:2 2T = 0.5m ḣ+ 0.5 I ̇ θ(Ε30)Η δυναµική ενέργεια του εξεταζόµενου συστήµατος (συσσωρεύεται είτε ως ενέργειαπαραµόρφωσης σε παραµορφώσιµα στοχεία, π.χ. ελατήρια, είτε ως ενέργεια εξ αιτίας τουβαρυτικού πεδίου) ισούται µε:U = m g h(Ε31)Η προσφερόµενη στο σύστηµα ισχύς (οφείλεται στο εξωτερικά ασκούµενο αίτιο) ισούται µε:Pt= F u̇ (Ε32)Η διαχεόµενη (καταστρεφόµενη) στο σύστηµα ισχύς (ενέργεια διαχέεται είτε σε στοιχείααπόσβεσης είτε λόγω τριβών) είναι µηδενική, διότι στο σύστηµα δεν υπάρχουν στοιχείααπόσβεσης ή τριβές:Pc= 0(Ε33)Τα εµπλεκόµενα κινηµατικά µεγέθη είναι η κατακόρυφη µετατόπιση h της µάζας Μ, ηκατακόρυφη µετατόπιση u της δύναµης F και η γωνία θ της τροχαλίας. Ωστόσο, η γεωµετρία- 19.16 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευώντης τροχαλίας υπαγορεύει το συσχετισµό µεταξύ των µεγεθών u,θ και h,θ. Ειδικότερα,ισχύουν οι ακόλουθες σχέσεις:h = rθ(Ε34)καιu = Rθ(Ε35)Συνεπώς, εµφανίζονται 3 κινηµατικά µεγέθη (u,h,θ) και 2 εξίσωσης συσχέτισης αυτών τωνµεγεθών. Εποµένως, το σύστηµα εµφανίζει 3-2=1 ανεξάρτητο κινηµατικό µέγεθος.Ισοδύναµα, το εξεταζόµενο σύστηµα διαθέτει 1 Βαθµό Ελευθερίας. Μπορούµε να επιλέξουµεαυθαίρετα ένα από τα προαναφερθέντα κινηµατικά µεγέθη ως Βαθµό Ελευθερίας (ΒΕ). Έστωότι επιλέγουµε τη γωνία θ ως (ΒΕ). Τότε θα ισχύει:( ̇ ) 22 2 2θ ̇ θ ̇ θ ( )T = 0.5m r + 0.5 I = 0.5 mr + IU = m g rθPt= F Rθ̇(Ε36)(Ε37)(Ε38)Εφαρµόζοντας την Ενεργειακή Αρχή Lagrange για τον (ΒΕ) q = θ , η ενεργειακή µεταβλητήLagrange L του συστήµατος προκύπτει ίση µε:2 2L = T − U = 0.5 ̇ θ ( mr + I ) − m g rθ(Ε39)Συνεπώς, ισχύουν και τα ακόλουθα:∂ L =2( mr + I )̇ θ∂ ̇ θ(Ε40)d ⎛ ∂L ⎞ d = (( mr ) ) + I ̇ θ = ( mr 2 + I )̇̇⎜ ⎟θdt ⎝ ∂ ̇ θ ⎠ dt(Ε41)⎛ ∂L⎞− ⎜ ⎟ = m g r⎝ ∂θ⎠(Ε42)∂P C= 0∂ ̇ θ(Ε43)∂P t= F R∂ ̇ θ(Ε44)Αντικαθιστώντας στην εξίσωση (Ε28), προκύπτει:2mr + I ̇̇ θ + m g r = F R(Ε45)( )Η εξίσωση (Ε45) αποτελεί την εξίσωση κίνησης του εξεταζοµένου συστήµατος. Ταυτίζεται,δε, µε την εξίσωση ισορροπίας ροπών του συστήµατος.Παρατήρηση: Εάν η µάζα M τρ της τροχαλίας δεν είναι αµελητέα, τότε, θεωρώντας ότι ητροχαλία βρίσκεται σε ένα σταθερό ύψος Η ως προς το επίπεδο µηδενικής δυναµικήςενέργειας, η δυναµική ενέργεια του συστήµατος καθίσταται ίση µε:U = m g h + Mτρg H(Ε46)Ωστόσο, επειδή το ύψος Η είναι χρονικά σταθερό και ανεξάρτητο της γωνίας θ, ο όροςMτρ g H αποτελεί µία σταθερά στη µεταβλητή Lagrange L του συστήµατος, συνεπώς δενσυµµετέχει στις παραγωγίσεις (βλ. Ε40,Ε41,Ε42), άρα, τελικά, δεν συµµετέχει και στηνεξίσωση κίνησης του συστήµατος.- 19.17 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και ΚατασκευώνΕφαρµογή: Γερανός µε φορείο κινούµενο επί σταθερού βραχίοναΈστω η διάταξη του Σχήµατος 8, στην οποία ένα φορείο µάζας Μ κινείται οριζόντια και προςτα δεξιά, επί βραχίονα, ο οποίος βρίσκεται σε σταθερό ύψος h. Από το κέντρο βάρους τουφορείου αναρτάται αβαρές και µη-ελαστικό συρµατόσχοινο, στο ελεύθερο άκρο Ρ του οποίουείναι σταθερά προσδεδεµένη µάζα m. Ζητείται η εξίσωση κίνησης του εξεταζοµένουσυστήµατος, χρησιµοποιώντας την Ενεργειακή Αρχή Lagrange, θεωρώντας ότι κατά τηνκίνηση του φορείου το µήκος L του συρµατοσχοίνου παραµένει σταθερό (δηλαδή, η κίνησητου φορείου δεν συνοδεύεται µε ταυτόχρονη ανύψωση ή απόθεση της µάζας m) καιαµελώντας τις τριβές.Σχήµα 8: Γερανός µε φορείο κινούµενο επί σταθερού βραχίοναΗ κινητική ενέργεια του εξεταζόµενου συστήµατος ισούται µε:2 2 2̇ ̇ ̇ (Ε47)T = 0.5 M u + 0.5m x + 0.5m yΗ δυναµική ενέργεια του εξεταζόµενου συστήµατος ισούται µε (έστω επίπεδο µηδενικήςδυναµικής ενέργειας για Y I =0):U = M g h + m g y(Ε48)Η προσφερόµενη στο σύστηµα ισχύς (οφείλεται στο εξωτερικό αίτιο F το οποίο θέτει σεκίνηση το φορείο) ισούται µε:Pt= F u̇ (Ε49)Η διαχεόµενη στο σύστηµα ισχύς είναι µηδενική, διότι στο σύστηµα δεν υπάρχουν στοιχείααπόσβεσης ή τριβές:Pc= 0(Ε50)Στις εξισώσεις (Ε47-Ε50), τα εµπλεκόµενα κινηµατικά µεγέθη είναι οι µεταβλητές u, x και y.Ωστόσο, από την Ενότητα 3 (Short notes) των Εκπαιδευτικών Σηµειώσεων, είναι γνωστό ότιοι εξισώσεις θέσεως του σηµείου Ρ είναι:x = u − l sinϕ ⎫ ⎧ẋ= u̇− l ̇ ϕ cosϕ⎫⎬ ⇒ ⎨ ⎬y = h − l cosϕ ⎭ ⎩ ẏ= l ̇(Ε51)ϕ sinϕ⎭Συνεπώς, συνολικά εµπλέκονται 4 κινηµατικά µεγέθη (u,x,y,φ) και 2 εξίσωσης συσχέτισηςαυτών των µεγεθών. Εποµένως, το σύστηµα εµφανίζει 4-2=2 Βαθµούς Ελευθερίας.Μπορούµε να επιλέξουµε αυθαίρετα δύο από τα προαναφερθέντα κινηµατικά µεγέθη. Έστω- 19.18 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και Κατασκευώνότι επιλέγουµε την οριζόντια µετατόπιση u και τη γωνία φ. Σε αυτήν την περίπτωση, οιεξισώσεις (Ε47-Ε50) γράφονται ως εξής:Κινητική ενέργεια εξεταζόµενου συστήµατος:( ̇ ϕ ϕ ) ( ̇ ϕ ϕ )22 20.5 0.5 cos 0.5 sinT = M u̇ + m u̇ − l + m l(Ε52)∆υναµική ενέργεια εξεταζόµενου συστήµατος:Προσφερόµενη ισχύς:∆ιαχεόµενη ισχύς:( cos )U = M g h + m g h − l ϕ(Ε53)Pt= F u̇ (Ε54)Pc= 0(Ε55)Για την εύρεση των εξισώσεων κίνησης του εξεταζοµένου συστήµατος, θα πρέπει ναεφαρµοσθεί η Ενεργειακή Αρχή Lagrange∂ ⎛ ∂L⎞ ⎛ ∂L⎞ ⎛ ∂Pc⎞ ⎛ ∂Pt⎞⎜ ⎟ − ⎜ ⎟ + ⎜ ⎟ = ⎜ ⎟∂t ⎝ ∂q̇ ⎠ ⎝ ∂q ⎠ ⎝ ∂q̇ ⎠ ⎝ ∂q̇⎠δύο φορές (µία για τη µεταβλητή u και µία για τη µεταβλητή φ). Ειδικότερα, θα ισχύει:Α. Για την ανεξάρτητη κινηµατική µεταβλητή q = uΓια τον αδρανειακό όρο:( )∂Lq= u ∂L∂ T −U⎯⎯→ = =∂q̇ ∂u̇ ∂u̇2{( 0.5 M u̇0.5m( u̇l ̇ ϕ cosϕ ) ( ) ) ( ( ))}2 0.5m l ̇ ϕ sinϕ 2M g h m g h l cosϕ(Ε56)∂= + − + − + − ⇒∂u̇∂L⇒ = M u̇+ m( u̇− l ̇ ϕ cosϕ)(Ε57)∂u̇Παραγωγίζοντας ως προς το χρόνο, προκύπτει:∂ ⎛ ∂L⎞ ∂2⎜ ⎟ = ( M u̇ + m( u̇ − l ̇ ϕ cosϕ )) = M u̇̇ + mu̇̇− ml ̇̇ ϕ cosϕ + ml ̇ ϕ sinϕ(Ε58)∂t ⎝ ∂u̇⎠ ∂tΓια τον όρο ελαστικότητας:∂Lq= u ∂L∂ ( T −U)− ⎯⎯→− = = 0(Ε59)∂q ∂u ∂uΓια τον όρο διάχυσης:∂PCq=u ∂PC⎯⎯→ = 0(Ε60)∂q̇∂u̇Για τον όρο διέγερσης:∂Pt q=u ∂Pt ∂ ∂Pt⎯⎯→ = { F u̇} ⇒ = F(Ε61)∂q̇ ∂u̇ ∂u̇ ∂u̇Αντικαθιστώντας στην εξίσωση (Ε56) µε τις εξισώσεις (Ε58-Ε61), προκύπτει:2M u̇̇ + mu̇̇ − ml ̇̇ ϕ cosϕ + ml ̇ ϕ sinϕ= F(Ε62)- 19.19 -

Μηχανισµοί & Εισαγωγή στο Σχεδιασµό Μηχανών – Ακαδηµαϊκό έτος: 2011 - 2012©Ε.Μ.Π. – Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο ∆υναµικής και ΚατασκευώνΒ. Για την ανεξάρτητη κινηµατική µεταβλητή q = ϕΓια τον αδρανειακό όρο:∂Lq= ϕ ∂L∂ ( T −U)⎯⎯⎯→ = =∂q̇∂ ̇ ϕ ∂ ̇ ϕ2{( 0.5 M u̇0.5m( u̇l ̇ ϕ cosϕ ) ( ) ) ( ( ))}2 0.5m l ̇ ϕ sinϕ 2M g h m g h l cosϕ∂= + − + − + − =∂ ̇ ϕ( m( u̇l ̇ ϕ cosϕ )( l cosϕ ) m( l ̇ ϕ sinϕ )( l sinϕ))= − − + =⎛⎜⎝̇⎞̇̇ ⎟⎠2 2 2 2= − mlu cosϕ + ml ϕ cos ϕ + ml ϕ sin ϕ =( ̇ ( ))̇ ̇= − mlu cosϕ + ml 2 ϕ cos 2 ϕ + sin 2 ϕ = − mlu cosϕ + ml2 ϕ ⇒∂L2⇒ = − mlu̇cosϕ+ ml ̇ ϕ∂ ̇ ϕΠαραγωγίζοντας ως προς το χρόνο, προκύπτει:∂ ⎛ ∂L⎞⎜ ⎟ = − mlu̇̇cos∂t⎝ ∂ ̇ ϕ ⎠+ mlu̇̇ sin + ml ̇̇Για τον όρο ελαστικότητας:∂Lq= ϕ ∂L∂ ( T −U)− ⎯⎯⎯→− = =∂q∂ϕ∂ϕ2ϕ ϕ ϕ ϕ2{( 0.5 M u̇ 0.5m( u̇l ̇ ϕ cosϕ ) ( ) ) ( ( ))}2 0.5m l ̇ ϕ sinϕ 2M g h m g h l cosϕ∂= + − + − + − =∂ϕ( m( u̇l ̇ ϕ cosϕ )( l ̇ ϕ sinϕ ) m( l ̇ ϕ sinϕ )( l ̇ ϕ cosϕ )) m g ( l sinϕ)̇( )= − + − =̇ ̇ ̇ ̇2 2 2 2= mluϕ sinϕ − ml ϕ sinϕ cosϕ + ml ϕ sinϕ cosϕ − m g l sinϕ⇒(Ε63)(Ε64)∂L⇒ − = mlu̇ ̇ ϕ sinϕ − m g l sinϕ(Ε65)∂ϕΓια τον όρο διάχυσης:∂PCq=ϕ ∂PC⎯⎯⎯→ = 0(Ε66)∂q̇∂ ̇ ϕΓια τον όρο διέγερσης:∂Pt q=ϕ ∂Pt ∂ ∂Pt⎯⎯⎯→ = { F u̇} ⇒ = 0(Ε67)∂q̇∂ ̇ ϕ ∂ ̇ ϕ ∂ ̇ ϕΑντικαθιστώντας στην εξίσωση (Ε56) µε τις εξισώσεις (Ε64-Ε67), προκύπτει:2− mlu̇̇ cosϕ + mlu̇ ̇ ϕ sinϕ + ml ̇̇ ϕ + mlu̇̇ ϕ sinϕ − m g l sinϕ= 0 ⇒⇒ − mlu + mlu ̇ + ml ̇̇ − m g l =2̇̇ cosϕ 2 ̇ ϕ sinϕ ϕ sinϕ0(Ε68)Οι εξισώσεις (Ε62) και (Ε68) αποτελούν τις εξισώσεις κίνησης του εξεταζοµένουσυστήµατος.Παρατήρηση: Εάν κατά την κίνηση του φορείου, πραγµατοποιείται ταυτόχρονα καιανύψωση του φορτίου, τότε η ποσότητα L (µήκος συρµατοσχοίνου) µεταβάλλεται µε το χρόνο(άρα συµµετέχει στις χρονικές παραγωγίσεις).- 19.20 -