THE Q-HOMOTOPY ANALYSIS METHOD (Q-HAM) - IJAMM

62
Int. J. of Appl. Math and Mech. 8 (15): 51-75, 2012.
M. A. El-Tawil and S. N. Huseen
∑ (
Equation (23) is a family of approximation solutions to the problem (18) in terms of the
convergence parameters .
)
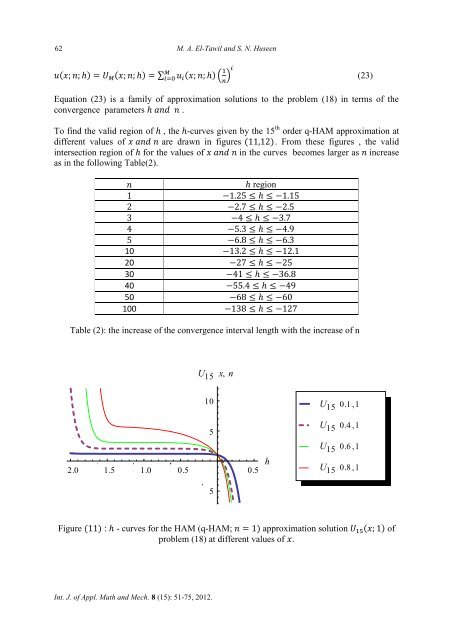
To find the valid region of , the -curves given by the 15 th order q-HAM approximation at
different values of are drawn in figures . From these figures , the valid
intersection region of for the values of in the curves becomes larger as increase
as in the following Table(2).
10
20
30
40
50
100
region
Table (2): the increase of the convergence interval length with the increase of n
U 15 x, n
2.0 1.5 1.0 0.5 0.5 h
10
5
5
U 15 0.1 ,1
U 15 0.4 ,1
U 15 0.6 ,1
U 15 0.8 ,1
Figure : - curves for the HAM (q-HAM; approximation solution of
problem (18) at different values of .
(23)