THE Q-HOMOTOPY ANALYSIS METHOD (Q-HAM) - IJAMM

70
solutions
3.0
2.5
2.0
1.5
Int. J. of Appl. Math and Mech. 8 (15): 51-75, 2012.
M. A. El-Tawil and S. N. Huseen
0.5 1.0 1.5 2.0 2.5 3.0
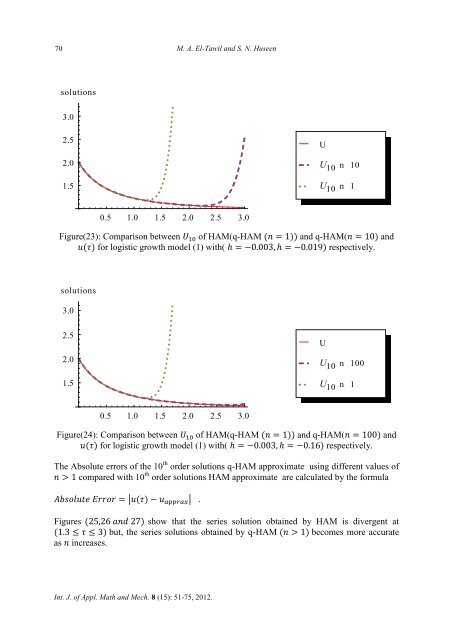
Figure(23): Comparison between of HAM(q-HAM and q-HAM( and
for logistic growth model (1) with( respectively.
solutions
3.0
2.5
2.0
1.5
0.5 1.0 1.5 2.0 2.5 3.0
Figure(24): Comparison between of HAM(q-HAM and q-HAM( and
for logistic growth model (1) with( respectively.
The Absolute errors of the 10 th order solutions q-HAM approximate using different values of
compared with 10 th order solutions HAM approximate are calculated by the formula
| | .
U 10 n 10
U 10 n 1
Figures show that the series solution obtained by HAM is divergent at
but, the series solutions obtained by q-HAM becomes more accurate
as increases.
U
U
U 10 n 100
U 10 n 1