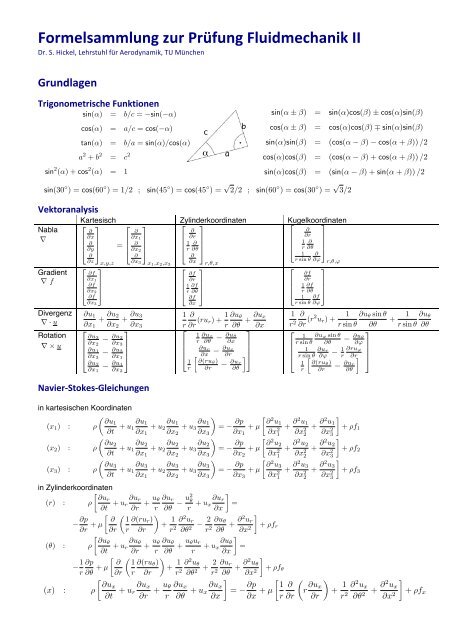
Formelsammlung zur Prüfung Fluidmechanik II

A Mathematischerr Anhang sin ⇤⇥ r, ,⇥ 

71 

A Mathematischer Anhang ⇤⇤ 

⌅ 

71 

A.3 Trigonometrische Funktionen 

0 30 45 Di 60erential-Vektoroperator 

90 

⇥ ⇧ ⇤x⇧f 

⌅ ⌅ ⇤ ⇤ ⇧r ⌃ 

Divergenz 

72 

⇤y 

sin( ) 0 1/2 2/2 3/2 1 

AA.3 Mathematischer 

Vektoranalysis Kartesische Koordinaten: 

⌅ f = ⌥ 1 ⌅⇧f 

⇧ 

A Mathemati 

⇤r 

⇧⇤ ⌃ 

A.3 Vektoranalysis 

⌅Anhang⌅ ⇥ 

⇤z⇧fx,y,z 

71 

cos( Formelsammlung ) 1 3/2 2/2 1/2 zur 0 ⇤ 

A Mathematischer 

Prüfung Fluidmechanik sin( ) = Anhang b/c = II sin( ) 

Di 

tan( 

erential-Vektoroperator 

⌅ ⌅ 

Di Dr. ) S. erential-Vektoroperator 

Hickel, 0 Lehrstuhl 3/3 für Aerodynamik, 1 3 TU München 

A Mathematischer Anhang 

⇥ ±⇤ = ⇧ ⇧x 

⇤x 

Zylinderkoordinaten: 

⇤ 

In Zylinderkoordinaten div 

⌃ ⇤ cos( ) = a/c = cos( 

71 

) 

⇤y ⌅ u (r, ⇥· ⇤,x) u In Kugelkoordinaten ⇥ (r, ⇤, ⌅) 

A.3 Kartesische Vektoranalysis 

Koordinaten: 

⇤ 

Kartesische Koordinaten: 

⇥ 

⇤⇤ 

⌅ A.3 Vektoranalysis 

⇥ 

⇤z x,y,z 

tan( ) = b/a = sin( )/cos( ) 

⇤ 

Di 

A.3 

erential-Vektoroperator 

In kartesischen 

Grundlagen sin( Trigonometrische ) cos( 

Koordinaten 

) 

(x, y, z) 

Funktionen 

a 2 + b 2 = c 2 

⇥ = ⇧ ⇤ 

⇥ = ⇧ ⇤⇤r 

⌅ 

⇧f 

1 ⇤ ⌃⇧f 

⇤x 

Di erential-Vektoroperator 

⇥ 

Kartesische ⇤ ⇤ 

⇤y = ⌃ 

0 Koordinaten: 

⌅ 

⇧ ⇤x 


⇧r 

⇤ r ⇤⇥⌅⇧r 

72 ⇤ 

⇤ 

0 1 


⇥ · u sin 2 ( )+cos 2 ( ) = 1 

Trigonometrische ⇥= ⇤u ⌃ 

⌅ f = ⌥ 1 ⇧f 


⇤ ⇤y ⌅ 1 

⌅ 

+ ⇤u 2 

+ ⇤u ⇧ r ⇧⇤⇥ 

⌃ 

⌅ f = ⌥ 1 ⇧f 

⇧⇤x 

r ⇧⇤ r, ,x ⌃ 

3 

⇤ 

⇤⇧f 

⇤ 

Kartesische Koordinaten: 

⇤z Funktionen 

30 1/2 ⇤ x,y,z ⇤z⇤x 3/2 1 ⇤x 2 ⇤x 

x,y,z 

3 

⇥ 

⌅ sin( ⌅ ) = b/c = sin( ) sin( ± ⇥) = sin( )cos(⇥) (A.1) ± cos( )sin(⇥) 

45 ⇥ = ⇧ ⇤x 

⇥ = ⇧ 1 ⇧f 

⇤r ⇧x 

Kugelkoordinaten: r sin ⇤ ⇧⌅ 

72 1 ⇤ ⌃ 

A Mathematischer ⇤ 

In 2/2 ⇤ ⌃ 

⇤ r ⇤⇥⌅ 

2/2 

⌅ ⇤ ⇤y ⌅ 

A.3 Vektoranalysis 

cos( ) = a/c = cos( ) cos( ⇥ = ⇧ ⇥ Anhang 

In ⇤x 

Zylinderkoordinaten: (r, ⇤,x) In Kugelkoordinaten ⇤ (r, ⇤, ⌅) 

⇤ 

⇤ 

⇥ 

± ⇥) 

⌃ 

= cos( )cos(⇥) (A.2) ⇥ sin( )sin(⇥) 

60 3/2 ⇤ 

⇤ ⇤y ⌅ 

⇥ ⇤z · u = 1 1/2 ⇤⇥ 

x,y,z 

90 1 tan( r ⇤r (ru r)+ 1 ⇤u 

+ ⇤u ⇤x r, ,x 

⇤ 

x 

0) = b/a r ⇤= Di sin( erential-Vektoroperator 

⇤x )/cos( ) sin( )sin(⇥) ⇤z x,y,z = (cos( (A.3) ⇥) cos( + ⇥)) /2 

⇥ = ⇧ ⇤ 

⇥ = ⇧ ⇤r 

⇤ ⌅ 

⇤ ⌅ Rotation b 

1 ⇤ ⌃ 

⇧f 

⇤r 

1 ⇤ 

⇥ 


InAKugelkoordinaten ⇤ r 

⇧ ⇧f c 

⇤ r ⇤ 

In Zylinderkoordinaten ⌃ 

⇤r 

(r, ⇤,x) 

⌅ 

⇧r 

Kugelkoordinaten: 

1 ⇤ 

⇤ ⌃ 

⇤⇥ ⇤ ⌅ 

Mathematischer 

⇥ 

a 2 ⇤⇥⌅ 

⇥ 

r sin ⇤⇥ 

⌅ f = ⇤ ⌥ 1⌅⇧f 

⇧r 

r, ,⇥ 

⇧f⇧ 

r ⇧⇤ ⌃ 

+ b 2 (r, Anhang = 

, ⇥) ⌅ f = ⌥ 1 ⇧f 

⇤ 

c 2 Kartesische ⇧ Koordinaten: 

r⇤ 

⇧⇤ α ⌃ a 

⇤ 


cos( )cos(⇥) = (cos( (A.4) ⇥)+cos( 71 

⇧r 

+ ⇥)) /2 

⇤x 

⇧f 

sin 2 ⇤x 

⇤ r, ⇥ 

⇥ 

( )+cos 2 ( ) = 1 sin( )cos(⇥) = (sin( (A.5) ⇥)+sin( + ⇥)) /2 

⇥ = ⇧ ⇤r 

⇥ · u = 1 ,x⇤r, ,x 

1 ⇤ ⌃ 

A.3 ⇤ r ⇤⇥ sin( Vektoranalysis 

⌅ ± ⇥) = sin( )cos(⇥) ⇥ ± = ⇧ ⇤ 

r 2 ⇤r (r2 u r )+ 1 ⇤u ⇥ = sin 

⇧ ⇤r 1 ⇧f 

+ 1 

⌅ f = ⌥ 1 ⇧f 

rot u ⇤⌅⇥u 

⇧x 

1 ⇤ 

⇧ 

⌃ ⇤u 

r ⇧⇤ ⌃ 

r sin ⇤ ⇧⌅ ⇤ r ⇤ ⌅ Divergenz 72 

Kugelkoordinaten: ⇧f 

r sin ⇤ 1 

⇤xr ⇤sin 

⇤ 

cos( ⇤ 

)sin(⇥) 

⌃ 

(A.6) 

sin(30 )=cos(60 )=1/2 ; sin(45 )=cos(45 )= ⌅ 2/2 ; sin(60 )=cos(30 )= ⌅ ⇤ 

⇤ ⇤y ⌅ 

⇥ = ⇧ ⇤r 

In Kugelkoordinaten ⇧x 

1 ⇤ 

⇥ 

(r, 

⇥ 

⇤, ⌅) 

r sin ⇤⇥ r, ,⇥ 

⌃ ⇤ r ⇤⇥⌅ 

⇤ 

3/2 

In Kugelkoordinaten ⇤ 

⇤x 

⇤ 

⇤ 

cos( 

r, 

± 

,x 

⇥) = cos( )cos(⇥) ⇥ sin( ⇤z)sin(⇥) x,y,z 

⇤x 

Gradient 

In Zylinderkoordinaten r, (r, ,x ⇤,x) (A.7) 

⇥ Di = erential-Vektoroperator 

⇧ ⇤r 

⇥ Kugelkoordinaten: Vektoranalysis ⇤ 

= ⇧ ⇤r (r, ⇤, ⌅) ⌅ Rotation 

In kartesischen Koordinaten (x, y, z) 

⇧f 

1 

⇤ 1 ⌃⇤ 

⌃ 

⇤ ⌅ 

⇤ 

div u ⇥· u 

r ⇤ 

⇧r⌅ 

r ⌅⇤ 

⌅ Divergenz 

⇧u 

⇧f 

⇤ 3 ⇧u 

⌅ 2 

Kartesische ⌅ f sin( = ⌥)sin(⇥) 1 ⇧f 

1 ⇤1 

⇤ = (cos( ⇥) cos( + ⇥)) /2 0 30 45 60(A.8) 

90 

Kartesisch Koordinaten: Zylinderkoordinaten: 

Kugelkoordinaten: ⇧f 

⇧ 

⇧r 

r sin r⇤⇥ 

sinr 

⇥⇧⇤ 

⇤⇥ 

⌃ 

⇧x 2 ⇧x 3 

Zylinderkoordinaten Kugelkoordinaten 

72 

⌅ ⌅ 

⇤ ⇥ 

⇥ 

⇥ 

⇥ 

Nabla cos( )cos(⇥) = (cos( ⇥)+cos( + ⇥)) /2 sin( ) 0 A Mathematischer ⇧r 

⌅ f = ⌥ 1 ⇧f r, ,⇥ r, ,⇥ 

1/2 2/2 3/2 (A.9) 1 

⌅ ⌅ 

⇥ = ⇧ ⇧ r ⇧⇤1 

⌃⇧f 

⌅⇥u = ⌥ ⇧u 1 ⇧u 3 

Anhang 

⇤r 

⇤ 

⇤ 72 In kartesischen 

⇤ 

⌅ f = 

rot ⇧⌥ 

Koordinaten 1⇧x ⇧f u 3 ⇤⇤⌅⇥u 

⇧x 1 ⌃(x, y, z) 

1 ⇤ ⌃ ⇤ sin( r )cos(⇥) = (sin( ⇥)+sin( + ⇥)) /2 cos( ) 1 3/2 2/2 1/2 (A.10) 0 

⇥ = ⇧ ⇤x 

⇤ 

⌅⇤ 

⌃ 

⌅ ⌅ 

1 ⇤ ⇤y ⌅ = ⇧ ⇤x 1 

⇤ ⌃ ⇤ ⇤x 2 ⌅ 

⇥ = ⇧ ⇤r 

1 ⇤ ⌃ 

⇥ A Mathematischer A 

1r sin ⇧f⇤ 

⇧⌅ 

grad f ⇥f 

⇧ r ⇧⇤⇤r 

⌃ 

div ⇧ 

u⇧f 

⇤⇥· u 

Divergenz Divergenz 

⌃ 

⇤ r ⇤ ⌅ 

⇥ · u = ⇤u ⇧u 2 

1 

⇤ ⇧xr 

+ ⇤u ⇧u 1 

r sin ⇤ ⇧⌅ 

⇧x 1 ⇧x 2 2 

⇤ ⌅+ ⇤u 3 

In Zylinderkoordinaten r sin ⇤⇥ ⇤ (r, ⇤,x) 

tan( ) 0 

r, ,⇥ 

⇤ 

⇤ 

3/3 ⇤x 1 1 

⇤x 

⇤ 21 ⇤x 3 

Rotation 

In kartesischen Koordinaten (x, Iny, Zylinderkoordinaten 3 ±⇤ 

In kartesischen (A.11) 

⇤z x,y,z ⇤x 3 x 1 ,x 2 ,x 3 

⇤x 

r sin ⇤⇥ 

⇤ ⌅ 

Koordinaten (x, In y, Zylinderkoordinaten z) 

(r, ⇤,x) In 

z) 

Kugelkoordinaten (r, 

(r, 

⇤, 

⇤,x) 

Rotation 

r, ,x 

r, 

⌅) 

,⇥ 

⇧f ⇥ 

In kartesischen ⇤Koordinaten ⌅ ⌅(x, y, In z) Zylinderkoordinaten ⇤ 

(r, 

⌅ 

,x) ⌅ 

Gradient 

Divergenz Zylinderkoordinaten: 

⇧r ⇤f 

⇧f 

⇧f 

Kugelkoordinaten: 

⌅ f = ⌥ 1 ⇧f 

0⇧ 

r ⇧⇤ ⌃30 ⇥ 45 60 90 

⇥ Divergenz 

⇥ f = ⇧ ⇤x 1 

div udiv u 

⇧r⇥· u⇥· u 

⇧r 

⇤f ⌃ 

⇥ · u ⇤u ⇧u 3 

1 

⇧f ⇤ ⇤x⇤ 

⌅ ⌅ 

sin( ) 0 1/2 2/2 3/2 1 

⇥ = ⌅ ⇧ 2 ⌅ 

⌅ f 1 ⇧f+ ⇤u ⇧u 2 

2 

+ ⇤u 3 

⇥ · u 1 1 ⇧u x 

⇤ 

r ⇧⇤⇤⌃ 

⌅ f 1 ⇧f 

⇤x 1 ⇤x 2 ⇤x 3 

r ⇤r (ru r)+ 1 ⇧u 

⇧x 2 ⇧x 3 

r ⇧⇤ ⇧x 

⇤u 

+ ⇤u x 

⌅⇥u = ⌥ ⇧u 1 ⇧u 3 

rot 

⇧x ⇤f ⇤r 

1 ⇤ ⌃⌅ cos( ) 1 ⇤3/2 r ⇤ ⌅ 2/2 1/2 

⇥ 0 

= ⇧ u⇧ 

⇤⌅⇥u ⇧x rot 3 u ⇧x ⇤⌅⇥u 

1 ⌃ ⌅⇥u = ⌥ ⇧u r ⇧u 

r ⇧⇤ ⌃ r 

x 

⇧ ⇧x ⇧r⇤ 

⌦⌃ 

⇤x 

⇧u ⇧f ⇤r 

1 ⇧f 

In kartesischen In kartesischen Koordinaten Koordinaten ⇤x 3 (x, y, (x, z) In y, Zylinderkoordinaten z) 

2 ⇧u ⇤ (r, 1 

1 ⇧(ru ) ⇧u 

⌃ ,x) In Kugelkoordinaten sin ⇤(r, ⇧⌅ , ⇥) r 

A Mathematischer Anhang ⇧x 1 ⇧x 2 r ⇧r ⇧⇤ 75 

In Kugelkoordinaten (r, ⇤, ⌅) 

Divergenz 

div u ⇤ ⇥· r ⇤ u ⌅ 

⌅ ⇤ 

In ⌅ 1 ⇤ 

div u ⇥· u 

tan( ) 

⇤ 

0 3/3 ⇤x⌅ 

In Kugelkoordinaten (r, ⇤, ⌅) 

⇥ · u 

⇥ 

= 

· u ⇤u = ⇤u 1 

⇧f+ ⇤u 1 

+ ⇤u 2 

r, + ⇤u 2 

,x 1 + ⇤u 3 

3 3 ⇥ ±⇤ · u = 1 ⇤ 

r sin ⇤⇥ 

⌅ 

r, ,⇥ Rotation 

⇤x 

⇤x 

1 ⇧r ⇤x 1 ⇤x 

2 ⇤x 2 ⇤x 3 3 

r ⇤r (ru r)+ 1 ⇤u 

+ ⇤u x 

⇥ · u = 1 ⇤ 

r ⇤ ⇤x r 2 ⇤r (r2 u r )+ 1 ⇤u sin 

+ 1 ⇤u 

In kartesischen Koordinaten (x, y, In (x, z) Zylinderkoordinaten y, z) 

(r, ⇤,x) 

A Mathematischer ⇤ Anhang In Kugelkoordinaten (r, ⇤, ⌅) 

⌅ 

r sin ⇤ 75r sin ⇤ 

⇧u ⇤ 

⇧f 

In kartesischen Rotation ⌅Kugelkoordinaten: 

f = ⌥ 

⇧ 

Koordinaten 1 ⇧f 3 ⇧u 2 

⌅ 

⇤ 

⌅ 

A.5 (x, y, z) 

r ⇧⇤ ⌃ 

⇧r 

In Zylinderkoordinaten 

In Zylinderkoordinaten 

Navier-Stokes-Gleichungen ⇧x 2 

⇧u 3 ⇧x 

(r, 

3 

,x) 

(r, ⇧u 2 ,x) In Kugelkoordinaten 

in 1 ⇧u 

(r, 

Komponentenschreibweise 

⇤ 

⌅ 

x ⇧u 

, ⇥) 

1 ⇧u ⇥ sin ⇤ ⇧u 

· ⇤u 1 

+ ⇤u ⇤ 

2 

+ ⇤u ⇥ 


1 ⇧f 

Divergenz ⌅ f 1 ⇧f 

⌅⇥u = ⌥ ⇧u r ⇧⇤ ⌃ 

r sin 3 

⇥ ⇤x= ⇤ ⇧⌅ 

⇥ · u ⇤r 

1 ⇧f 

1 ⇤x 1 2 ⇤ ⇤x ⌃ 3 

⇥ · u = ⇤u 1 

+ ⇤u 2 

+ ⇤u 3 rot u ⇤⌅⇥u 

⇥ · u = 1 ⇤ 

1 1 

⇧x 2 ⇧u 3 

⇧x 3 

r ⇧⇤ ⇧x 

r sin ⇤ ⇧⇤ ⇧⌅ 

74 ⇧ ⇧x 3 

⇤ 

r sin ⇤ 

r ⇤r (ru r)+ 1 ⇤u 

+ ⇤u x 

r ⇤r (ru ⇧x 

⌅⇥u = ⌥ ⇧u 1 1 ⌃⇧u 3 

r)+ 1 ⇤u 

+ ⇤u x 

⇥ · u 1 ⇤ 

r ⇤ ⇤x r ⇤ r ⇤ r⌅⇤ 

⇤x 

2 ⇤r (r2 u r )+ 1 Gradient ⇤u sin 

+ 1 ⇤u 

⇧u ⇧ 2 ⇧x 3 ⇧u 1 ⇧x 1 ⌃ 

⌅⇥u = ⌥ ⇧u r ⇧u x 

A Mathematischer 

⇧ ⇧x ⇧r ⌦⌃ 

⌅⇥u = ⌥ 1 ⇧u r 1Anhang 

⇧ru ⇥ 

A.5 In kartesischen Navier-Stokes-Gleichungen Koordinaten (x 1 ,x 2 ,x 3 ) 

⇧x ⇧⌅ 

1 ⇧x 2 

in Komponentenschreibweise 

⇧ r sin ⇤ ⇧⌅ r ⇧r⌦ 

⌃ 

⇧u 2 ⇧u 1 

1 ⇧(ru ) ⇧u r sin r ⇤ r sin 

⇤x 

1 ⇧(ru ⇤ ) ⇧u 1 ⇤x 2 ⇤x r 

⇧x 3 

Rotation 

1 ⇧x 2 

r ⇧r ⇧⇤ 

r ⇧r ⇧⇤ 

1 

⇤ 

InA.4 Kugelkoordinaten 

Zylinderkoordinaten kartesischen Kugelkoordinaten Navier-Stokes-Gleichungen Koordinaten r(r, (r, (r, 

sin , ⇤⇥ ⇥) 

⇤,x) , ⇥) 

in Komponentenschreibweise 

r, ,⇥ 

In Zylinderkoordinaten div u ⇥· (r, u,x) 

Navier-‐Stokes-‐Gleichungen 

1 ⇤ 

⇤r (ru r)+ 1 ⇤u 

+ ⇤u Rotation 


x 

⇥ · u 

⇤ 

r ⇤ ⇤x 

⇥ · u = 1 ⌅ 

⇧u⇤ 

Divergenz 

in kartesischen Koordinaten In kartesischen Koordinaten (x, y, z) r ⇤r (ru r)+ 1 ⇤u 

+ ⇤u 3 ⇧u 2 

x 

⇥ · u = 1 = ⇤ 

rot u ⇤⌅⇥u 

⇧x 2 ⇧x 

r 2 ⇤r (r2 u r )+ ⇤u sin 

+ 1 ⇤u 

2 ⇤r (r2 u r )+ 1 ⇤u sin 

+ 1 

grad f ⇥f 

In Zylinderkoordinaten (x 1 ) : ⇤ ⇥ ⌅u (x ⇥ 

1 

(r, ⇤,x) In⌅ 

Kugelkoordinaten (r, ⇤, 

⇤u 

⌅) 

1 ⇧u x ⌅t + u ⌅u 1 ⌅u 1 ⌅u 1 

⇧u 

1 Gradient + u 2 + u 3 = ⌅p ⇤ ⌅ 2 ⌅ 

1 ,x 2 ,x 3 ) 

u 1 

+ µ 

⌅x ⇤ 

1 ⌅x 

r ⇧⇤ ⇧x r sin ⌅ 2 ⌅x 

⇤ ⇤ 3 ⌅x 

r sin ⇤ Vektoridentitäten: 

1 ⌅x 

⌅ 

2 + ⌅2 u 1 

1 ⌅x 2 + ⌅2 u 1 

2 ⌅x 2 + ⇥f 1 

3 

In kartesischen Koordinaten (x 1 ,x 2 ,x 3 ) 

⌅⇥u = ⌥ ⇧u r 1 ⇧u ⇧u x x 

r sin 

⇧u 

1 ⇧u 

⇤ r sin 

⇥ sin ⇤ ⇧u 

3 

(x r ⇤ ⇤x 

2 ⇧ ⇧x ⇧r 


In Kugelkoordinaten (r, , ⇥) 

⌅⇥u = Koordinaten ⌥ ⇧u 1 ⇧u 3 (x, y, z) 

1 

⇥ ⌅u ⇥ 

2 

r ⇧⇤ ⌦⇧x 

⌃ 

r sin ⇤ ⇧⇤ ⇧⌅ 

⇧(ru ) ⇧u r 

⇥ · u = 1 ⇤ 

r 2 ⇤r (r2 u r )+ 1 ⇤u sin ⇥ · u = 

+ 1 ⇤u 1 

⇤u + ⇤u 2 

+ ⇤u In Kugelkoordinaten 

rot u⇧ 

⇤⌅⇥u ⇧x 3 ⇧x 1 ⌃ 

⌅⇥u = 

grad f 

⇥ 

r⌥ 

⇧u⌅t + u ⌅u 2 ⌅u 2 ⌅u 2 

1 + u 2 + u 3 = ⌅p ⇤ ⌅ 2 ⌅ 

u 2 

+ µ 

r ⇧u x 

⌅x 1 ⌅x 

⇧r ⇧⇤ ⌅⇥u = 2 ⌥ ⌅x 1 

⇧u r ⌅x 1 ⇧ru 

1. ⇥ 

⌅( + ⇥) =⌅ 

⇧u (r, , ⇥) 

3 

⇤f 2 ⇥f 

+ ⌅⇥ 

⇧u 1 


Gradient ⇧ ⇧x ⇧r ⌦⌃ 

⇧ r sin ⇤ ⇧⌅ r ⇧r⌦ 

⌃ 

Koordinaten (x, y, z) 

⇤x 

r sin ⇤ r sin div 1 ⇤x 

⇤ u ⇥· 2 ⇤x 

u 3 

⇥ · u = 1 ⇧x 1 ⇧x 2 

Gradient 

(x 1 : 1 

2 ⌅x 

1 

⇧(ru ) ⇧u 

⇤ 

In Zylinderkoordinaten (r, ,x) 

r ⇤r (r2 u r )+ ⇤u sin 

+ 1 ⇤u 

⌅ 

⇧u 3 ⇧u 2 

In kartesischen Koordinaten (x, y, z) In Zylinderkoordinaten 

⇥ f = ⇧ ⇤x r 

1 ⇧(ru ) ⇧u r 

1 

In Kugelkoordinaten r(r, ⇤, ⇧r ⌅) ⌅t 1 

1 

1 

2 + ⌅2 u 2 

1 ⌅x 2 + ⌅2 2 

2 ⌅x 2 + ⇥f 2 

(x 1 ) : ⇥ ⌅u ⇥ 

1 

3 

1 

⇧⇤ 

r 

⇧r 

⇧⇤ 1 ⇤f 

2. ⌅(c )=c⌅ ⌅2 1 

⌃ 

⌅2 1 

(x 3 ) : ⇥ ⌅u ⌅t + u ⌅u 1 ⌅u 1 ⌅u 1 

1 + u 2 + u 3 = ⌅p ⇤ ⌅ 2 ⌅ 

u 1 

+ µ 

⌅x 1 ⌅x 2 ⇥⌅x 3 

3 

⇤ ⇤x ⌅, mit (r, c 1 

⌅t + u ⌅u 3 ⌅u 3 ⌅u 3 

1 + u 2 + u 3 = ⌅p ⌅x 1 ⇤ ⌅x 2 + ⌅2 u 1 

⌅ 2 u 3 

+ µ 

⌅x 1 ⌅x 2 ⌅x ⇤,x) = const 

⇤ 

In⌅ 

kartesischen Koordinaten (x, y, z) 

⇤f 

r sin ⇤ r sin ⇤ 

⇧x1 

2 

⇧u⇧x ⇥3 

sin ⇤ ⇧u 

⇤ ⌅ 

⇤x⇤ 

⌅ 

In Kugelkoordinaten (x 2 ) : ⇥ 

⌅⇥u = 

⇧u r sin 1 ⇤ ⇧u 

(r, ⌅u ⇥ 

⌅x 3 

2 

⇧⇤ 3 

⇤, ⌅) ⇧⌅ 

Gradient In kartesischen 

⇧ ⇧x 

Koordinaten (x, y, z) ⇥ · u 1 ⇧u 3 ⇧u 2 

⇤ 

⇥ · u = ⇤u 1 

+ ⇤u 2 

+ ⇤u r ⇤r (ru r)+ 1 ⇤u 

+ ⇤u 1 ⇧u x ⇧u 

grad⇥ 

3 ⌅t + u ⌅u 2 ⌅u 2 ⌅u 2 

1 + u 2 + u 3 = ⌅p ⇤ 

⌅x 2 + ⌅2 1 ⌅x 2 + ⌅2 u 1 

u 3 

⌅ 2 1 ⌅x 2 + ⌅2 u2 

⌅ ⌅x 2 + ⇥f 1 

3 

3 

2 ⌅x + ⇥f 3 

(x 2 ) : ⇥ ⌅u ⇥ 

2 

3 ⌅ 

⌅t + u ⌅u 2 ⌅u 2 ⌅u 2 

1 + u 2 + u 3 = ⌅p ⇤ ⌅ 2 ⌅ 

u 2 

+ µ 

⌅x 1 ⌅x 2 ⌅x 3 ⌅x 2 u 2 ⌅x 

+ µ 

⌅x 1 ⌅x 2 ⌅x f 3 ⇥f ⌅x 2 

3 ⇧x 1 ⌃ 

⇤f 

⇧x 2 ⇧x r ⇧⇤ ⇧x 

⌅⇥u = ⌥ 1 ⇧u r 1 ⇧ru ⇥ 

3. ⌅( ⌅x ⇥) 

grad f ⇥f 3 

x 

⇧ 

⇤ Vektoridentitäten: 

2 + ⌅2 2 + ⌅2 u 2 

1u 2 ⌅x 

1 = ⌅x ⌅⇥ 2 + ⌅2 2 + ⌅2 u 2 

2u 2 ⌅x 2 + ⇥f 2 

3 

2 

⇥⌅ ⌅x 2 + ⇥f 2 

(x 3 ) : ⇥ ⌅u ⇥ 

3 

⇧u r sin 2 ⇤ ⇧u ⇧⌅ 1 r ⇧r 

⇧x ⇧x 2 

⌅⇥u = ⌥ ⇧u 1 ⇧u ⇧ 

r ⇤ Gradient ⌅⇥u 

⇧x 3 ⇧x 1 ⌃ ⇤x 

= ⌥ ⇧u r ⇧u 

⌦ ⌃ 

⌅ 

x 

⇧ ⇧x ⇧r 

⇥ f = ⇧ ⇤x 

1 ⇧u 1 

⇥ sin ⇤ ⇧u 

⇥ 

(x 3 ) : 1 ⇧(ru ⇥ ⌅u ⇥ 

3 

) ⇧u ⇤f 

r 

⌃ 

⌦⌃ 

r sin ⇤ ⇧⇤ ⇧⌅ 

⇥⇥ ⇥⇥ 

r ⇧r ⇧⇤ 3 ⇤ ⇤x ⇧u 2 ⇧u 1 

1 ⇧(ru ) ⇧u 

In kartesischen ⌅t + u ⌅u 3 ⌅u 3 ⌅u 3 

1 + u 2 + u 3 = ⌅p ⇤ ⌅ 2 ⌅ 

⌅t + u ⌅u 3 ⌅u 3 ⌅u 3 

1 + u 2 + u 3 = ⌅p ⇤ ⌅ 2 ⌅ 

u 3 

+ µ 

⌅x 1 ⌅x 2 ⌅x 3 + 

⌅x 

µ 3 

u 3 

⌅x 

Koordinaten (x, y, 

r 

Zylinderkoordinaten 

in Zylinderkoordinaten ⇤x (r, ⇤,x) 1 ⇤x 2 ⇤x 

In 

z) 

2 ⌅ 

Kugelkoordinaten ⇤f⇧x 1 (r, ⇧x 2 , ⇥) 

r ⇧r ⇧⇤ 

In kartesischen ⌅⇥u Koordinaten = ⌥ 1 ⇧u r 11. 1 ⌅x 

⇧ru⌅( ⇥ + ⇥) 2 ⌅x 

=⌅ 3 ⌅x 

+ ⌅⇥ 3 4. ⌅ ⌅x 2 + 

⌅x ⌅22 + ⌅2 u 3 

u 3 

⇥ 1 

= ⌅x 2 + ⌅2 u 

1 ⌅x 2 + ⌅2 u 3 

2 3 

2⇥ ⌅x 2 + 

⌅x 

⇥f 2 + ⇥f 3 

3 


2 3 

⇧ r sin ⇥ ⇤ ⇧⌅ (x, y, z) r ⇧r 3 ⌦ ⌃ ⇤x 3 

⇤ ⇥⇤f⇤ ⌅ grad f ⇥f 

1 ⇧u 

In Zylinderkoordinaten (r, ,x) ⇥ · u = 1 ⇤ 

In kartesischen⇥ Koordinaten · u = 1 ⇤ 

(x, y, z) 

r ⇤r (ru r)+ 1 ⇤u 

+ ⇤u r 2 ⇤r (r2 u r )+ 1 ⇤u sin 

+ 1 

x ⇧u In Zylinderkoordinaten (r, ⇤,x) In Kugelkoordinaten (r, ⇤, ⇤u ⌅) 

Vektoridentitäten: ⇤f 

grad f ⇥f 

r ⇧⇤ ⇧x 

⇥ r sin ⇤ r sin ⇤ 

⌅⇥u = ⌥ ⇧u r ⇧u x 

⇤ 

⌅ 

⇤ 

⌅ 

1 ⇧u x ⇧u 

1 ⇧u ⇥ sin ⇤ ⇧u 

⇥ f = ⇧ f ⇤x = ⇧ 1 ⇧(ru ) ⇧u r 

5. ⌅ · (a + b) =⌅ · a + ⌅ · b 

⇤x 1 r 

⌅ur 

⇧r 2. ⇧⇤⌅(c )=c⌅ , mit c = const 

(r) : 

1 

⇤f ⇥ 

⌃ 

⇧⇤f 

⇤ ⌃⇤x ⇧x 2 ⌅⌅t + u ⌅u r 

r 

⌅r + u ⌅u r u 2 ⌅ 

r ⌅ r + u ⌅u r 

x = 


⌅x 

In Zylinderkoordinaten (r, ⇤ ⇧r ,x) 

1. ⌅( + ⇤ ⇥) ⌦⌃ 

⇥ x r ⇧⇤ ⇧x 

r sin ⇤ ⇧⇤ ⇧⌅ 

⇤x=⌅ 1 2 ⌅⇤f 

⇧(ru 

+ 

) 

⌅⇥ 

6. ⌅⇥(a + b) =⌅⇥a + ⌅⇥b 

⌅p 

⇧u r 

3. ⌅( ⇥) = ⌅⇥ + ⇥⌅ 

r ⇧r ⇧⇤ r ⇤ ⇤x 


⇥ 

⌅⇥u = ⌥ ⇧u r ⇧u x 

⌅⇥u = ⌥ 1 ⇧u r 1 ⇧ru ⇥ 

⇤f ⇤x ⌅ 

Vektoridentitäten: 3 

⇧ ⇧x ⇧r ⌦⌃ 

⇧ r sin ⇤ ⇧⌅ r ⇧r⌦ 

⌃ 

⇤x 

⇤f 3 

⌅r + µ 1 ⌅(ru r ) 

+ 1 ⌅ 2 ⌅ 

u r 2 ⌅u 

⇥ 

2. ⌅(c In Kugelkoordinaten )=c⌅ ⇤ 

⌅r r ⌅r r 2 ⌅ 2 r 2 + ⌅2 u r 

⇥ f = ⇧ , mit c = 

⇤x 1 

(r, const , ⇥) Gradient ⇥⇥1 

⇧(ru ⇥⇥) 

⇧u 7. ⌅(a · b) =(a · 1⌅)b ⇥⇧(ru +(b ) · ⌅)a ⇧u r + a ⇥⌅⇥b + b ⇥⌅⇥a 

In Kugelkoordinaten ⌅ur 

⇤f 

(r, ⇤, ⌅) 4. ⌅ ⇥ 

= r ⇥ ⇧r ⇧⇤ 

r ⇧r ⇧⇤ 

1. ⌅( : 

+ ⇤f ⌃ ⇤ ⇤x 2 ⌅ 

⇥ ⇤f · u = 1 ⇤ 

⇤x 3 

r 2 ⇤r (r2 u r )+ 1 ⇤u sin 

+ 1 ⇤u ⇥ f = ⇧ ⇤x 1 

⇤⇥) ⇥ =⌅ ⌅⇥ 

2 

⌅t + u ⌅u r 

r 

⌅r + u ⌅u r u 2 

⌅ ⌅x 2 + ⇥f r 

⇤ 

⇤ ⌅u ⌅ur 

⌅ r + ⌅u r 

( ) ⇥ x = 

⌅x 

3. ⌅( ⇥) = ⌅⇥ ⇤f 

1 + ⇤⇧u ⇥⌅ ⌅t + u ⌅u 

r 

⇥ sin ⇤ 

⌅r + u ⌅u 

+ u u ⌅ 

(r) : ⇥ 

r ⌅u 

⌅t + u ⌅u r 

r 

⌅r + u ⌅u r u 2 ⌅ 

⇧u In Kugelkoordinaten (r, ⇤, ⌅) 

⌃ ⇤ ⇤x 2 

r sin ⇤ ⇧⇤ 

⇥ ⌅p 

⌅ ⇧⌅ 5. 

⇥ 

r r⌅ 

⌅ r r + + u u ⌅u r 

x x = = ⌅p ⇤ ⇥ 

⌅ 

⌅x ⌅x ⌅r + µ 1 ⌅(ru r ) 

+ 1 ⌅ 2 u r 2 ⌅u 

⌅r r ⌅r r 2 ⌅ 2 r 2 + ⌅2 u r 

⌅ ⌅x 2 

⇤ ⇤ ⌅ · (a + b) =⌅ · a + ⌅ · b 

r sin ⇤ r sin ⇤ 

⇤f 

⌅⇥u ⌥ 1 ⇧u r 1 ⇧ru ⇥ 

⇤ 

Vektoridentitäten: 

2. ⌅(c )=c⌅ ⌅ 

⇥⇥ ⇥⇥ , mit c = const 

4. ⌅ 

grad ⇤x 3 

f ⇥f 

⇧ 

sin ⇤ ⇧⌅ r ⇧r⌦ 

⌃ 

1 ⇧u ⇥ sin ⇤ ⇧u 

⇥ 

= ⌅r + µ 1 ⌅ 

⇥ 

⌅r r ⌅r (ru r) 

1 ⌅ 2 ⌅ 

1 ⌅p ⌅ u r 2 ⌅u 

2 2 r 2 ⌅2 u r 

⌅ ⌅x 2 + ⇥f r 

r ⇥ 2 

1⇤ ⌅ 

+ µ 1 ⌅(ru ) 

+ 1 ⌅ 2 u 

⌅r 

⌅r r 

⇧(ru ) 

r sin ⇤ ⇧⇤ ⇧⌅ 

⇧u r 6. ⌅⇥(a + 2 ⌅ 

b) =⌅⇥a 2 + 2 ⌅ 

⌅u ⌅u r 

r 2 + ⌅2 u 

( ) : ⇥ 

⌅ 

r ⌅u ⇧r ⇧⇤ ⌅⇥u = ⌥ 1 ⇧u r 

+ ⌅⇥b 

1 ⇧ru ⇥ 1. ⌅( + ⇥) =⌅ + ⌅⇥ 

5. 3. ⌅ Gradient ( ⌅( · (a ): + ⇥) b) = =⌅ ⇥ ⌅⇥ · a ⌅ ⇥⌅· b 

⇧ r sin ⇤ ⇧⌅ r ⇧r⌦ 

⌃ 

⌅t + u ⌅u 

r 

⌅r + u ⌅u 

+ u u ⌅x 2 + ⇥f 

⌅t + u ⌅u 

r 

⌅r + u ⌅u 

+ u u ⌅ 

r ⌅u 

+ u x = 1 ⇤ ⇥ 

⌅p ⌅ 

r ⌅ r ⌅x r ⌅ 

+ µ 1 ⌅(ru ) 

+ 1 ⌅ 2 u 

⌅r r ⌅r r 2 ⌅ 2 + 2 ⌅u r 

r 2 + 

⌅ 

⇤⇤ ⌅ux 

r 

In r kartesischen ⌅ r Koordinaten 1 ⇧(ru ⌅x ) ⇧u 

⇥ ⇤ 

⌅t + u ⌅u x 

r 

⌅r + u ⌅ 

⌅ux 

⌅u x ⌅u x 

(x) : ⇥ 

+ u x = 

(x, r y, z) 

7. ⌅(a r ⌅ ⌅x 

· b) =(a · r⌅)b ⇧r +(b · ⌅)a ⇧⇤ + 2. a⌅(c ⇥⌅⇥b )=c⌅ + b, ⇥⌅⇥a mit c = const 

Vektoridentitäten: 1 ⌅p 

⇤⌅t + u ⌅u x 

r 

⌅r + u ⌅ 

⌅u x ⌅u x 

+ u x = ⌅p ⇤ 1 

⇥⇥ ⇥⇥ 

6. ⌅⇥(a + b) =⌅⇥a + ⌅⇥b 

⇥ 

4. ⌅ ⇥ 

= ⌅ 

⇥ 2 

⇤f 

r ⌅ 

+ µ 1 ⌅ 

⌅r r ⌅r (ru ) 1 ⌅ 2 u 

r 2 ⌅ 2 

2 ⌅ 

⌅p 1 ⌅u r 

⇥ f = ⇧ ⇤x 1 

r grad 2 ⌅2 u 

⌅ ⌅x 2 + ⇥f 

⌅x + µ ⌅ 

r ⌅u ⇥ r ⌅ ⌅x 

x 

+ 1 ⌅ 2 ⌅ ⌅x + µ ⌅ 

r ⌅u ⇥ 

x 

+ 1 ⌅ 2 ⌅ 

u x 

r ⌅r ⌅r r 2 ⌅ 2 + ⌅2 u x 

⌅x 2 + ⇥f x 

u x 

⇤ r ⌅r ⌅r r 2 ⌅ 2 + ⌅2 u x 

3. ⌅( ⇥) = ⌅⇥ + ⇥⌅ 

1. + ⇥) =⌅ + ⌅⇥ Vektoridentitäten: ⇤f ⌃ f ⇥f 

7. 5. ⌅(a ⌅ · b) (a =(a + b) · =⌅ ⌅ux ⌅)b +(b · a + · ⌅)a ⌅ · b a ⇥⌅⇥b + b ⇤ ⇥⌅⇥a 

(x) : ⇥ 

⇤x 2 ⌅ 

⇥ 

⌅t + u ⌅u x 

r 

⌅r + u ⌅⌅x 2 + ⇥f x 

In Kugelkoordinaten (r, ⇤, ) 

⌅u x ⌅u x 

+ u x = 

r ⌅ ⌅x⇤f 

4. ⌅ ⇥ 

= 

⇥⇥ ⇥⇥ 

⇥ 2

lströmungen ! 

Eine komplexe 25 Zahl z = x+iy repräsentiert einen Vektor mit den Komp 

¯z = x iy re i 

2 Potentialströmungen 

z ¯z = |z| 2 = r 2 

y 

"! x z=x+iy 

Kapitel 1 

Wirbel-Strömu 

z1 

¯z = Kartesische |z| 2 r 2 

Re 

Koordinaten Polarkoordinaten 

1z = 1 

Komplexe Zahlen 

z = re 1 i = 1 ¯z 

re i = 1 ¯z = 

r2 |z| ¯z 

2 = ¯z 

"! x 

! 

daß die imaginäre Einheit i= ⌅ 1 die zweite Komponente des Vektor 

! 

! 

z=x+iy 

könneny 

Re 

z=x!iy 

¯z = 

r2 |z| 2 = 

z ¯z ¯z 

!"! x 

der reellen 

"! x 

Analysis entsprechende Operationen definiert 

"! x werde 

wird als C = {x +iy|x, mit z yRe 

⇤= R} x + , iy, i = i 2 ⌅ = 

x, y ⌅ R Re 1, bezeichnet. 1, {F, z} 2 C; {x, y, 

r, ⌅ R 

Eine Funktion f(z) =f R (x, y)+if z I ¯z (x, y) nennt z man analytisch, wenn f R und f I stetig di erenzierbar sind 

Im 

z=x!iy 

Eine und die Funktion Cauchy-Riemann-Di f(z) =f R (x, y)+if erentialgleichungen I (x, y) nennt man erfüllen. analytisch, wenn f R und kartesische f I stetig di erenzierbar Darstellung 

z = x z=x!iy +iy 

z = re 

sind 

Wirbel-Strömungen 

i 

"! x Man kann eine komplexe eine ! zweidimensionale Zahl in kartesischen Potentialströmung Koordinaten oderin inder 

Pol 

vonRe 

F 

und Einedie Funktion Cauchy-Riemann-Di f(z) heißt y konform, erentialgleichungen wenn z=x+iy x, f(z) y ⌅analytisch R erfüllen. ist und f ⇥ (z) r, ⇧= 0gilt. ⌅z=x!iy 

R Die 

x, 

Abbildung 

y ⌅ Rz=x!iy 

"! z ⇥ x (z) in z existiert, muß dF/dz unahängig 

Re(z) 

z ⇥ = 1.1 =x 

f(z) Definitionen r, ⌅ R r = |z| = und x 2 + yG 

2 vo 

Re z=x! 

einmal 

Eine ist dann Funktion winkeltreu f(z) heißt und es konform, gilt ⇥ = wenn . z f(z) = x +iy analytisch ist und f ⇥ (z) z ⇧= = 0gilt. re i 

Diez Abbildung = x +iy Im(z) 

dz = 

z ⇥ z ⇥ =y 

dx wählen und 

= f(z) z = re i erhält 

= atan y x 

x, y ⌅ R x, y ⌅ R r, ⌅ R r, = arg(z) 

ist dann winkeltreu und es gilt ! 

⇥ = . Re(z) =x r = |z| x 2 + yRe(z) 2 =x Als e i ⌅ R 

Wirbel 

x, 

bezeichnet 

y ⌅ R 

= r = cos |z| + = i sin x 2 + ⇤ y 2 |e i man | =1 eine drehen 

z z = x +iy z = 

z=x!iy 

x 

"! x Im(z) =y 

= atan y x 

Re 

= +iy 

arg(z) polare z = re 

z’ Darstellung 

i dF 

Im(z) =y z=x!iy 

z re i 

dz Begri 

= @ @x = des +i@ z 

atan@x Wirbels = y ist daher eher intui 

z 1 Wirbel-Strömungen 

x 

1.1 Definitionen S1 

und Grundbegri e i = cos + i sin e 

z’ 

= x , 

arg(z) +iy 

x, Re(z) y ⌅ R=xDie letzte Re(z) Zeile =x r = bezeichnet r, |z| = ⌅ R xman ⇤ |e i S 

2 + r y= als 2 |z| Eulersche = x 2 + Relation y 2 . 

f(z) 

| 1=1 

x, y ⌅ R e i = cos + i sin eines⇤ Wirbels |e i | =1 bedeutet nicht notwendig 

S1 

! 

z = Im(z) x +iy =y Das konjugiert 

SIm(z) =y Komplexe = z atan = re yi 

von z = erhält atanman y durch Spiegelung an der x-Achse: 

x = arg(z) 

f(z) 

1 

x = r, arg(z) ⌅Re(z) R =x r = 

oder man wählt dz =idy und erhält 

Die Als letzte Wirbel Zeile bezeichnet man man eineals Eulersche Relation . 

z=x!iy ! drehendeDie Bewegung Re(z) letzte=x eZeile i von Fluidelementen bezeichnete r manum alsein !’ Eulersche gemeinsames Relation Zentrum. . Der 

Die ¯z = x 

i z = x +iy 

= cos + i sin ⇤ |z| cos |e= i + 

Zirkulation iy = re 

!’ 

i xi 2 sin + y 2 ⇤ |e i z = reIm(z) i =y = 

| =1 | =1 

Re(z) =x eines Geschwindigkeitsfeldes dF 

u bezglich der Kontur S, 

Das Begri konjugiert des Wirbels Komplexe ist daher voneher z erhält intuitiv manDas und durch Im(z) konjugiert mathematisch Spiegelung =y Komplexe nicht an S2derpräzise von x-Achse: = zatan erhält formulierbar. y man durch DasSpiegelung Vorhandensein 

der x-Achse: 

x, y ⌅ RS 

r, ⌅ R 

2 

definiert S als das Integral der Tangentialgeschwindigkeit entlang von S 

eines Wirbels 

2 

¯z = x z = bedeutet 

iy x = +iy Sre i nicht notwendigerweise, z = re 

2 

i daß Fluidelemente z ¯z = 

26 

rotieren |z| 2 Eulersche = müssen r 2 x = arg(z) r |z| = x 2 + ey i 2 = cos + i sin ⇤ 

Die letzte Zeile bezeichnet Die letzte Zeile man als bezeichnet Eulersche manRelation als Eulersche . Relation Relation . dz = 1 @ 

i @y + @ 

Im(z) =y 

= atan y 

e und umgekehrt : 

¯z = i = cos + i sin 

x iy = re i ⇤ |e i x 

| =1 

= arg(z) @y = @ i @ @y @y 

Das konjugiert Komplexe Das konjugiert von z Komplexe erhält manvon durch z erhält Spiegelung Die man 

Ausgewählte Re(z) =xRechenregeln 

1 

Wichtige elementare Funktionen sind: 

r = |z| = x 2 + y 2 

(S) u · ds . 

Wichtige 26 26 elementare z ¯z = Im(z) |z| 2 Funktionen = =y r 2 26 sind: = atan y x = arg(z) z ¯z = |z| 2 = r 2 z = 1 letzte durch ean i 

re i = 1 = der Zeile Spiegelung cos x-Achse: bezeichnet ¯z 

+ i sin 

¯z = 

r2 2 2|z| Potentialströmungen 

2 = ¯z an⇤ der|e man x-Achse: i | =1 als Eulersche Relation . 

Da dF/dz in beiden Fällen gleich sein muß, müss 

Die letzte Zeile bezeichnet man als Eulersche Relation . 

¯z = x iy = re ¯z i 

Das konjugiert Komplexe 

Die = xletzte iy Zeile = rebezeichnet i man als 

konjugiert 

Eulersche Relation (2.5) zerfüllen. ¯z von 

S komplexe 

. Aus 

z erhält 

diesen 2 Potentialströmungen 

folgt 

man 

wiederum: 

durch Spiegelun 

1. die Exponentialfunktion: 

Das 

1 e i = cos + i sin ⇤ |e i | =1 

Zeile bezeichnetz = 1 konjugiert 

man re als i = 1 Komplexe ¯z 

1. die Exponentialfunktion: 

Eulersche r2 Relation |z| 2 ¯z von z erhält 

Zahl 

1 

man 

3. der Logarithmus: 

. z ¯z z = 1 durch Eine 

re i = 1 Spiegelung Funktion f(z) an 

n¯z ist = 

r2 |z| 

die 2 Oberflächennormale = ¯z der =fx-Achse: 

R (x, y)+if I (x, y) nennt man analytisch, wenn f R und 

z ¯z = |z| 2 = r 2 Das konjugiert 

z ¯z = |z| 2 = r 2 Komplexe von z erhält¯z man = xdurch iy Spiegelung = re an der x-Achse: 

@ 

3. 3. der der Logarithmus: 

e z = e x+iy = e e iy 

und die Cauchy-Riemann-Di z ¯z erentialgleichungen 

auf 2 i 

A und ds ist ein infinitesimales Kurvene 

¯z = erfüllen. 

1 x iy = re i 

3. der Logarithmus: 1 

iert Komplexe Eine Funktion von e z = z erhält e x+iy f(z) man = =f edurch x e R iy (x, Spiegelung y)+if I an (x, der y) x-Achse: Eine nennt Funktion man analytisch, f(z) Eine =f Funktion 

ln z = ln(re 

wenn f R und i ) = ln r +i = 

f I stetig di erenzierbar Um 

|z| +iarg(z) 

densind 

rotationsbehafteten 

+ i2⇤k 

Anteil u ( ) 

R (x, y)+if f(z) heißt I (x, y) konform, nennt man wennanalytisch, f(z) analytisch wenn fist R und f ⇥ I (z) stetig ⇧= 0gilt. di eren D 

z ¯z = |z| 

x iy = und re i die ln ln Cauchy-Riemann-Di 2 = r 

z = z = ln(re i ) i = ) = ln ln r +i r erentialgleichungen 2 z = 1 

re i = 1 ¯z ¯z r2 |z| 2 = ¯z 

z = 1 

re i = 1 ¯z ¯z = 

¯z = 

r2 |z| 2 x ¯z iy = re i 

z ¯z 

z ¯z = |z| 2 = r 2 @x 2 = @2 

@y@x = @2 

@y 2 ) =0 

z ¯z 

2. die trigonometrischen Funktionen: und die 

+i = ln = |z| z |z| = +iarg(z) ln(re i + erfüllen. Cauchy-Riemann-Di erentialgleichungen erfüllen. 

) = i2⇤k + ln i2⇤k 

+i mit = dem |z| +iarg(z) Hauptzweig + i2⇤k k =0und dem u ( 

k-ten ) trennen Nebenzweig zu A 

Eine Funktion 

ist dann winkeltreu und es gilt ⇥ = . 

können, k ⇤= 0. verwendet m 

2. Eine die trigonometrischen 1 

Funktion f(z) heißt Funktionen: konform, wenn f(z) analytisch ist und f ⇥ (z) ⇧= 0gilt. Die Abbildung z ⇥ ⇥ = f(z) 

|z| 2 = r 2 

1 ist mit 

re i = 1 mit dann dem dem cos ¯z winkeltreu z Hauptzweig = eiz + e iz 

Eine 

¯z = 

r2 |z| 2 = ¯z und es gilt ⇥ . 

cos z = eiz + e k iz 

k , =0und sin mit z = dem dem eiz e iz Funktion f(z) heißt konform, wenn f(z) analytisch Potentialfeld ist und f ⇥ (z) eindeutige) ⇧= 0gilt. DieHelmholtz-Ze 

Abbildung z ⇥ 

Um den rotationsbehafteten z = 1 f(z) Eine 

re i = 1 =f Funktion R (x, y)+if 

z ¯z 

¯z ¯z = 

Anteil r2 u ( |z| 

, sin z = eiz k-ten Hauptzweig ) 2 = ¯z 

= |z| 

f(z) I =f (x, 2 = 

y) 

r 

R (x, nennt 2 

y)+if man I (x, analytisch, 1 

y) nennt wenn man analytisch, f R f I wenn stetigfdi R und erenzierbar f I stetigsind 

di erenzierbar sind 

1 

und die Cauchy-Riemann-Di und die Cauchy-Riemann-Di erentialgleichungen 

k-ten der e Bewegung z ¯z 

iz Nebenzweig k =0und Eine eines 

erentialgleichungen erfüllen. 

k ⇤= kFunktion 0. ⇤= dem 0. k-ten ist komplex Nebenzweig di erenzierbar, k ⇤= 0. wenn 

2 

2i 

ist dann winkeltreuFluidelementes und es gilt ⇥ (FE) 

erfüllen. z 

z = 1 

re i = 1 ¯z ¯z = 

r2 |z| 2 = ¯z z = 1 

re i = 1 @ ¯z 2 ¯z 

= 

r2 |z| 2 = ¯z 

@y 2 = @2 

@x@y z = @2 

¯z @x 2 ) =0 

z ¯z = . vom rotationsfreien Anteil 

Ein gegebenes Geschwindigkeitsfeld läß 

u ( ) trennen Eine Eine 

z ¯z zuFunktion Funktion 

können, f(z) f(z) 

2 verwendet 

Eine =f heißt R Funktion (x, konform, 

man y)+if 

2i die 

f(z) I (ohne (x, wenn heißt y) f(z) 

weitere nennt konform, analytisch man Beachtung 

wenn analytisch, 

Eine ist f(z) und Funktion 

der 

analytisch fwenn ⇥ (z) 

Randbedingungen S ⇧= 

1 f 

f(z) 

R 

0gilt. ist und und 

=f 

fDie I fstetig R ⇥ (z) Abbildung (x, erfüllen 

bis 

⇧= di 

y)+if 

auf 

0gilt. erenzierbar also z 

ein 

Die I ⇥(x, jeweils zAbbildung ⇥ y) = sind f(z) nennt die Laplace zman n⇥ Sz ⇥ analyt = Gleich 

Eine Funktion f(z) =f 

f(z 

Eine Funktionistist komplex di Eine di erenzierbar, Funktionwenn 

ist wenn zkomplex di erenzierbar, wenn 

z’ 

ion f(z) =f R Helmholtz (x, y)+if I (x, y) Zerlegung nennt man analytisch, wenn f R und f I stetig di erenzierbar f ⇤ f(z) zf(z 0 ) 

f(z) 

1 

aber rotationsbehafteten Anteil u 

(z 0 ) = sind lim 

( ) ze 

Potentialfeld und ist 

eindeutige) die dann Cauchy-Riemann-Di winkeltreu 

Helmholtz-Zerlegung 

ist dann und es winkeltreu gilt erentialgleichungen ⇥ R (x, y)+if I (x, y) nennt man analytisch, wenn f R und f I stetig di erenzierb 

= 

: 

und . es gilt erfüllen. 

⇥ = und . die Cauchy-Riemann-Di Potentialströmungen ! erentialgleichungen ist =0eineerfüllen. 

Folge z’ der 

und die Cauchy-Riemann-Di erentialgleichungen erfüllen. 

z⇥z 0 z z 

uchy-Riemann-Di Jedes erentialgleichungen S 

0 

Ein 1 erfüllen. kann als Summe eines S 

f(z) 

1 Anteils 

ion f(z) fheißt ⇤ f(z) f(z 0 ) 

(z 0 und konform, ) = 

eines 

lim 

z⇥zwenn divergenzfreien f(z) analytischf ist ⇤ f(z) 0 ) 

f ⇤ gegebenes EineGeschwindigkeitsfeld Funktion 

f(z) f(z 

f(z) 

0 ) 

heißt S1 

Eine konform, läßt Funktion sich wenn in einen f(z) f(z) zrotationsfreien heißt analytisch konform, Eine ist Anteil und zwenn Funktion f ⇥ u f(z) ( ) ⇧= und analytisch 0gilt. f(z) ne 

einen 

Folge Die heißt divergenzfreien S 

f(z) ist Abbildung der 

und konform, z’ 

Rotationsfreiheit 

f 

(z 0 ) = lim 

(z 

Anteils und 0 ) ! = f ⇥ (z) lim 

dargestellt ⇧= 0gilt. Die Abbildung werden: unabhängig z ⇥ z ⇥ vom 

0 0 z z z = f(z) Weg der Annäherung z ⇥ z 

0 z 0 

z⇥z 0 z z 0 

u ⇥ (z) z ⇧= ⇥wenn existiert. = u ( 0gilt. z ⇥ ) = 1 f(z) Die 

der 

+ u ( ) z’ Abbildung analytisch Geschwindigke 

z ⇥istzu 

! 

, S 

⇥ 

aber rotationsbehafteten Anteil u ( ) 2 

ist dann winkeltreu und es Sist zerlegen: gilt ⇥ = . 

1 dann winkeltreu S 0 und es giltist ⇥ = dann . winkeltreu komplexen 

inkeltreu und es gilt ⇥ 1 

S und esPotentials gilt 

2 

= . 

Jede auf einem Kreisring konvergente 

!’ 

Laurentreihe 

S 

⇥ = F (z) . die Potentialfunktion 

f(z) 

1 

!’ 

f(z) 

1 stellt dort eine analytische Fun 

unabhängigvom vomWeg Weg der der Annäherung unabhängig z vom z ⇥z Der rotationsfreie z Anteil, mit ⇥ 0 u Weg z ( 0 ) existiert. =0 der ! Annäherung z z ⇥ z 

, ist der 

z’ 

Gradient einer S 0 existiert. 

Strömung 

mit: 

u = u ( ) + u ( ) , 2 Potentialfunktion u -> Potentialströmung 

Jedeauf auf einem Kreisring konvergente Jede S2 

auf einem Laurentreihe Kreisring stellt stellt konvergente dort dort eine eine Laurentreihe analytische 

⌅⇥ 

( dar. 

! z ) z’ = S2 

Wichtige elementare S 

(1.1) 

S 

2 

stellt Funktion 

Funktionen 

dort dar dar eine 

sind: 

!’ 

z 

!’ z’ 

In deranalytische komplexenFunktion Beschreibung dar definiert man eine 

S 

S 

1 

1 

S 

Sf(z) = a n z n . 

Der divergenzfreie Anteil, f(z) 

1 

1. ⌅ · u ( ) =0 ⇤ divergenzfreier 

mit: ⌅⇥ ⌅⇥ ! 

mit · ⌅⇥ 

u ( ) 1 

S 

=0 

f(z) 

1S 

2 

, ist im allgemeinen n= rotationsbehaftet ⌅ 

⇥ u ( S S 

f(z) ) 2 

1 

S ! 1. die Exponentialfunktion: 

F nach S1 

z: = -> Wirbelströmung 

ds 

Wichtige f(z) f(z) = = elementare a n az n . Funktionen f(z) sind: = a n z n n z n 2 

Wichtige elementare S 

! 

f(z) 

2 

. 

. !’ Funktionen sind: 

!’ ! 

Laurent-Reihen sind eine Verallgemeinerung2. der ⌅⇥u aus der ( ) !’ 

reellen =0 ⇤Analysis rotationsfreier 

1. ⌅ bekannte 

n= · n= u ( ⌅ 

) ⌅=0 ⇤ divergenzfreier n= Anteil, 

8 

S⌅ 

2 

1. Sdie Exponentialfunktion: 

Wichtige elementare 1. die Exponentialfunktion: Ein Zusammenhang e z = e x+iy S= ezwischen x e iy 

2 

Wichtige Funktionen elementare sind: 

w(z) Zirkulation = dF 

Funktionen 

und der Rotation von u ist g 

2 

Die komplexe sind: 

S2 

Integration entspricht dem Wegintegral in zwei Raumdimensionen. 

Laurent-Reihen 2. 

Wirbelströmungen 

⌅⇥u sind sindeine eine Verallgemeinerung Laurent-Reihen 

S 

( ) 2 

S 

dz = @ @x +i@ @x = u iv =(u r 

der sind der aus eine aus der Verallgemeinerung 

2 

der reellen reellen Analysis der bekannten aus der reellen Potenz-Reihen. Analysis Alsbekannten Wirbelstärke Potenz-Reihen. bezeichnet man die 

lementare Funktionen esind: 

z =0 

= e x+iy ⇤ rotationsfreier 

= e x e 

Die Die komplexe Integration entspricht Die komplexe iy Anteil. 

Integralsatz . Allgemein gilt für ein stetig di erenzierbares Geschwindigke 

1. die Exponentialfunktion: 1. die Exponentialfunktion: ekomplex z = e2. x+iy die integriert = trigonometrischen e x e iy muß man also zunächst den genauen Integrationsweg angeben 

dem dem Integration Wegintegral entspricht zwei in zwei Raumdimensionen. dem Wegintegral Wenn inWenn ⇥zwei man 

mit 

Funktionen: 

1. man Raumdimensionen. eine Starrkörperrotation z = eine re 

S i✓ 2 

Funktion , q = |w|, Wenn ↵ mit = man dem atan(v/u). eine Geschwindigkeitsf 

Funktion 

Als Definitionen Wirbelstärke Wichtige bezeichnet elementare man Funktionen die Rotation sind: des Geschwindigkeitsvektors: 

auf einem Gebiet A bis auf isolierte Singularitäten (Punkte z, in denen f(z) nic 

xponentialfunktion: 

komplex integriert muß muß man man komplex also ealso z = zunächst e x+iy Wichtige 

integriert = den eden x muß genauen man also Integrationsweg zunächst den angeben. u genauen · ds = Ist Ist Integrationsweg (⇥aber f(z) u) f(z) · n dA analytisch angeben. . ⇥ Ist aber ⇤ f(z) analytisch 

2. Wirbelstärke die trigonometrischen bezeichnet Funktionen: die Rotation 

2. 

⇥ des 

die trigonometrischencos bzw. ⇤ 8 umläuftZirkulation Funktionen: z = eiz + e iz 

, sin z = eiz e iz 

e z iy elementare Funktionen sind: 

= e x+iy = e x e iy 

der Integrationsweg ist 2 die über S keine die Fläche Singularität, 2iA integrierte, dann ist das Integral wegu 

auf e z auf = e x+iy einem = Geschwindigkeitsfeldes 

eGebiet x e iy AA1. bis bis die auf auf Exponentialfunktion: 

auf isolierte einem Singularitäten Gebiet 1. Adiebis Exponentialfunktion: Wichtige elementare Funktionen auf (Punkte isolierte z, in z, denen Singularitäten denen f(z) flächennormale f(z) nicht (Punkte nicht definiert definiert Wirbelstärke. 

z, ist) denen ist) und und tri f(z) 

Nach trit 

nicht = 

sind: 

t ⌅⇥u x 

Stokes’schem 

definiert ( ) = ist) ⌅⇥u 

Satz 

und= trirot t u = 

cos z = eiz + e iz 

⇥u 3 

, sin z eiz e iz ⇥u 2 

⇥ S 

A 

bzw. umläuft der = der ⌅⇥u Integrationsweg ( ) = 

bzw. 

⌅⇥u Sumläuft Skeine keine der Singularität, Integrationsweg ⇥x 2 ⇥x 3 

⇥x 1 

u 1 e 2 ⇥ 

y 

2. die trigonometrischen 1 

u(x) = ⌃ 

dann dann istSist das keine ⇤das Integral Singularität, kann ⇤sie wegunabhängig: 

alternativ dann ist ⇤durch das Integral Integration wegunabhängig: ⇤der Geschwindigkeit 

rigonometrischen Funktionen: 2 = rot u = ⌃ ⇥u 

2i 

b 

1 ⇥u 3 ⌥ 

⌅ ⇥x 3 ⇥x 1 ⇧ = 

⌅ x 1 ⇥ ⌥ 

cos z eiz + e iz 


⇧ 

Aus ⇥ 

e z = e x+iy 2. die 

= e x trigonometrischen 

Funktionen: 

e iy 

Funktionen: 

e z = e x+iy = e x e dem 

⇥x 

⇥u f(z)dz 

2 

2 

iy 

u 2 

1. Stokes’schen e die Exponentialfunktion: 

u 

2 

Integralsatz 2i resultiert (1.2) dann folgender Zusammenha 

entlang = der f(z)dz A unschließenden = f(z)dz = ···= Kontur S 

0 

f(z)dz berechnet = F (b) F (a) 

⇤ ⇤ 

werden 

cos z = eiz + e 

Wirbellinien iz ⇤ ⇤ 

cos 

, sin z = sind eiz e ⇤ 

Integralkurven iz ⇤ 

z = eiz + e iz 

⇤ ⇤ b 

2 

⇥x ⇤ b ⇥u 1 1. ⇥ 

⇤ tation Starrkörperrotation 

⇤ b 

1 ⇥x 2 ⇥x 3 

u 3 

deseGeschwindigkeitsfeldes: 

mit dem Geschwindigkeitsfeld 

cos 

, 

z = 

sin eiz z = + eiz e iz e iz 


2 

3 

2. die trigonometrischen 2. der Wirbelstärke 

S 

S 1 ⇥ S 2 ⇥⇤ 

Beispiel a 

f(z)dz 2 

f(z)dz 2i = = 

f(z)dz Funktionen: die trigonometrischen 2 

2i Funktionen: 2i e z = e x+iy = e x e iy 

= = ···= 

···= f(z)dz f(z)dz = = F f(z)dz = (b) F (b) F = (a) ···= F (a) f(z)dz = F (b) F (a) 

dx 

Beispiel 1 

= dx 2 

= dx Die Wirbelstärke beträgt dann (⇥ ist die Wink 

3 

(S) = u · ds x = · n dA ⇥. 

⇤ 

S S 1 S 1 S 1 2 S 2 3S 2 S 

S 1 a a S 2 a 

2 ⇥ 


, sincos z = z eiz = eiz e+ iz e iz 

, u(x) sin z = ⌃ 

eiz e iz 

S1 

S ⌅ x 1 ⇥ ⌥ 

A⇧ 

0 

2 

2i 2 2. die trigonometrischen 2i 

Funktionen: 

vergleiche mit Stromlinie 

S1S1 

S1 

dx 1 

Ganz analog zur Stromlinie definiert man die WirbellinieS 

als Integralkurv 

u 

2 

1 

= dx 2 

u 2 

= dx 0 

= ⌃ 

⌅ 0 ⌥ 

⇧ 

3 


u 2⇥ , sin z = eiz e iz − 

3 Die Wirbelstärke beträgt dann 2(⇥ ist die Winkelgeschwindigkeit) 2i 

dx 

S2S2 

S2 

Eine Wirbelfläche ist eine von Wirbellinien aufgespannte Fläche. ds = ⇥ (x(s),t) ⇤ 

0 2. Potentialwirbel mit dem Geschwindigkeitsfeld b 

Eine Wirbelröhre ist eine Röhre, deren Mantel aus Wirbellinien besteht. 

⇥ ⇤ 

Eine Wirbelröhre mit infinitesimal kleinem Querschnitt wird als 

x 

bWirbelfaden (s = ⌃ 

b⌅ 

0) 0 ⌥ 

= x⇧ 

0 . 

bezeichnet. b x S 

2 /r 2 

3 

2⇥ Man beachte, daß 

s ist 

Wirbelmodelle 

S3S 

der Kurvenparameter. u(x) = ⌃ 

in der vektoriellen 

3 

S3 

⌅ x 1 /r 2 ⌥ 

Darstellung d 

⇧ 

gespiegelten Geschwindigkeitsvektor enspricht. Da 

Festkörperrotation 

In der 

Potentialwirbel 

parameterfreien a Darstellung lautet diese0 

2. Potentialwirbel mit dem GeschwindigkeitsfeldDefinition: 

des physikalischen Geschwindigkeitsvektors in der 

mit der Winkelgeschwindigkeit Ω 

mit der Zirkulation Γ 

a a 

a 

dx 

Umläuft oder tri 1 

t= ein dx ⇥ 

2 

geschlossener = dx ⇤ 

3 

x . 

mitIntegrationsweg r = x 2 1 S, der ganz in A liegt, Sing 

2 3 

+ x2 2 . Die Wirbelstärke beträgt 

1 

Umläuft oder oder tri tri t ein t ein geschlossener Umläuft oder Integrationsweg tri t ein geschlossener S, S, der der ganz ganz in Integrationsweg 1Ain liegt, Af(z)df liegt, Singularitäten, = ⇥ 2 /r 2 

2 3 

2 

2 3 

3 

0 

u(x) = ⌃ 

S, ⌅ der 

x 1 /r 

⇥ 

ganz 2 ⌥ 

x x 2 

2 

so ⇧ist 

so in Aistliegt, Singularitäten, so ist 

! = 4 0 5 

S (p)Resf(z p ) . 0, r ⌅= 0 

1 1 

= 1 

⇥ S p ) f(z)df . = ⇥ f(z)df = ⇥ 2⇤i Analog 

u(x) 

zur 

= 4 

Stromfläche 0 definiert 

x 

man = 

2 die Wirbelfläche als eine von Wirbel 

p r 

2 1 

5 

u(x) = 4 x 1 

5 

2 

S 

0 

unbestimmt , r =0 

⇥0 

S (p)Resf(z ⇥ S (p)Resf(z p ) . 

2⇤i 2⇤i 

2⇤i p ) . 

Wirbelröhre als eine Röhre, deren Mantel aus Wirbellinien besteht. Als W 

p p 

p 

S S 

S 

Hierin istmit Wirbelröhre p der r = Index x 2 1 

mitder + infinitesimal x2 2 Singularität . Die Wirbelstärke Obwohl kleinem A, das Querschnitt, ⇥beträgt 

Geschwindigkeitsfeld S (p) die Umlaufzahl sodaß die Fluideigensch 

intuitiv dieser Singu auss 

Hierinististp pder der Indexder der Hierin Singularität ist p der in A, A, Index ⇥ S ⇥(p) S (p) der die die Singularität 

Residuum Umlaufzahl als in 

von 

dieser konstant A, 

f 

dieser ⇥ 

in S (p) 

z 

Singularität angenommen p . 

die Umlaufzahl 0, 

Koordinatenursprung) 

und und Resf(z werden Resf(z dieser r p 

⌅= ) können. das 0 p ) Singularitätüberall das und Resf(z identisch p ) das null. Ei 

= 

Residuumvon vonf fininz p z. 

p . Residuum von f in z p . 

Gegenüberstellung unbestimmt der Eigenschaften 

3. Rankine-Wirbel: , r =0der Wirbelstärke 

Man kann 

und 

sich 

der 

das 

Geschwind 

Modell ein 

2.3.2 Komplexe Darstellung zweidimensionaler Potentialström

f = ⌅ ⇥ ⌅G =0 

Kelvinschen Wirbelsatzes 

orher entstandenen Helmholtzschen Wirbelsätze lauten unter Verwendung der Zirkulation 

. Es wird vorausgesetzt, daß die Strömung reibungsfrei ist, daß die auftretende Volumenkraft 

hat und daß die Strömung barotrop ist. 

tzsche Wirbelsatz lautet: 

nsfreie Fluidelemente bleiben für alle Zeiten rotationsfrei. 

n Satz beweisen, indem man für eine beliebige das infinitesimal kleine Fluidelement umschließ 

infinitesimal kleine Fläche dA einschließt die Zirkulation 

1. barotrope Strömung und daher 

Koordinatenursprung) überall identisch null. Ein bestimmt Um (1.9) 

Fluidpartikel ⇥u werden für= diesen 

dreht ⇧soll. ⇥Fall sich⇥ Der . zu 

also von berechnen 

nicht. einem Punkt benötig au 

Um (1.9) für diesen Fall zu berechnen benötigt man noch eine Beziehung zwischen dx ⇥ und d , die aus 

3. Rankine-Wirbel: Man kann sich das Modell eines Fürrealen ein unbegrenztes Wirbels zusammengesetzt Gebiet V und denken unter ausder 

ein 

folgender Überlegung ⌅⇥ 

1 ⇥ 

radialen folgenderKomponente Überlegung rresultiert, bezeichnet. worinist l der der Ab W 

resultiert, ⌅p =0worin l der Abstand zwischen x ⇥ Festkörperrotation im Kern, r ⇤ r 0 und einemUm durch und 

ist, Potentialwirbel (1.9) dem P auf Schnittpunkt fürder diesen x-Achse 

hat (1.7) die ausserhalb Fall der ist. 

Lösungr>r zuSenkrechten 

berechnen Dieser Abstand 

0 : benötig w 

durch P auf der x-Achse ist. Dieser Abstand wird so gemessen, daß folgender r = er l< tan 0 ist, Überlegung ist wenn unabhängig > 

u ( ) (x) = 1 ⇥resultiert, 90 von : worin . Dannl ist der Ab 

Der Rankinewirbel r = l 

r ⇥ ⇥ 

2. tanf ist isteine unabhängig Potentialkraft von . uund Dann 

" 

daher ist 

ist ein realistischeres Modell eines Wirbels 

realer Wirbel durch P! 

auf der x-Achse 

4 

ist. 

⌅r⌅ 

Dieser 3 dV Abstand w 

bestehend aus einer Festkörperrotation im 

V 

dr = dl tan + ld 

dr = dl tan + ld 

rd 

rd 

r = l tan ist unabhängig cos 2 =0⇤ dl = 

von . Dann ist sin 

Kern und einem Potentialwirbel 

⌅⇥f 

außerhalb 

= cos 2 ⌅ ⇥=0⇤ ⌅G =0 dl = 

sin 2 

wobei l nimmt ⇥ ab, = ⇥(x wenn ) und x ⇥ zunimmt, r = x x . Gleichung (1 

des Kerns. In einem 

l nimmt 

realen 

ab, 

Wirbel 

wenn x 

verläuft ⇥ zunimmt, also : 

dr = dl tan + ld also : rd 

fester Bezugspunkt undcos x ein Punkt des Integr 

die Wirbelstärke jedoch im Gegensatz zum 

2 =0⇤ dl = 

sin 

die Aussage des Kelvinschen 

Rankine-Modell glatt. 

r r Ist die Wirbelstärke konzentriert r in einer r Kurve ( 

dx ⇥ = dl = rd Wirbelsatzes 

dx ⇥ = dl = rd 

0 

0 

sin 2 . 

l nimmt ab, wenn xsin ⇥ zunimmt, 2 . 

also : 

d 

ansonsten, vereinfacht sich das Volumenintegra 

Mit dieser dt =0. 

Mit dieser Beziehung 

Beziehung läßt Insich einem(1.9) realen nach Wirbel kurzer verläuft Rechnung die Wirbelstärke auswerten S: bei und rdx 0 iman ⇥ = Gegensatz erhält 

dl = rd läßt sich (1.9) nach kurze 

für zum Rankine-Modell glatt. 

sin 

Satz von Biot-‐Savart 

2 die Umfangskomponente 

Die historisch der Geschwindigkeit vorher Die Folgerungen entstandenen in einem dieser Zylinderkoordinatensystem, Helmholtzschen Beobachtungen lassen Wirbelsätze sich folgendermaßen das entlang des zusammenfassen: 

Wirbelfadens ds ⇥ r ausgerichtet 

. 

ponente der Geschwindigkeit einem Zylinderko 

⇥ 

Allgemein: Ein Wirbelfaden mit der Zirkulation Γ induziert die Geschwindigkeit: Mit ist: dieser lauten 

u(x) 

Beziehung unter Verwendung 

= 

läßt sich (1.9) der Zirkulation nach kurze 

Hierbei ist das Linienintegral ist: folgendermaßen. entlang Esdes Wirbelfadens S’ zu nehmen. 

4 ⌅r⌅ 3 1. wird Wirbel vorausgesetzt, haben in der Regel daß ein dierotationsbehaftetes Strömung reibungsfrei ponente Geschwindigkeitsfeld. der ist, Geschwindigkeit daß die auftretende 

S Als Sonderfall in einem Volumenkraft 

trittZylinderko 

Potent 

14 32 1 Wirbel-Strömungen 


u = (cos( 2 ) cos( 1 )) 

f ein Potential hat und auf, daß der die nur Strömung in seinem Ursprung barotrop r =0rotationsbehaftet ist. 

ist. 

u = (cos( 2 ) cos( 1 )) 

ist: 4⇥r 

(1.10) 

4⇥r Die Wirbelstärke zeigt gemäß folgender Abbild 

Umfangsgeschwindigkeit am Punkt P 2. für Nicht endlich alle rotationsbehafteten langen geraden Strömungen Wirbelfaden: stellen Wirbel dar. 

Das 

Für 

Vorzeichen 

die korrekten 

der Die 

Vorzeichen Der Zirkulation Wirbelstärke I. Helmholtzsche bestimmt 

muss 

zeigt 

die 

gemäß den 

Rechte-Hand-Regel Wirbelsatz ! Umlaufsinn folgender lautet: : Abbildung > 

beachtet 

0 bedeutet von 

werden. 

links Umlauf nach rechts 

u 

und 

= 

die Geschwindigkeit 

(cos( 2 ) cos( 

zeigt 1 

x)) 

die imZeichenebene math. pos. 4⇥r Sinn, hinein: 

3 

in 

Als Potentialfeld bezeichnet man ein Geschwindigkeitsfeld mit verschwindendem rotationsbehafteten An 

< 0 bedeutet Umlauf die Zeichenebene im math. neg. hinein: Sinn. Gemäß Definition 

teil: mit u ( ) = ⇧ und = ⇧⇥u ⇥ndA 

der komplexen ( ) berechnet. 

Zirkulation 

I 

= ⇧⇥⇧ =0 Da Die . über Wirbelstärke muß 

die-für zeigt den gemäß folgender Abbild Wir 

Potentialwirbel Satz 2 Rotationsfreie Fluidelemente bleiben Wirbelfaden für alle Zeiten rotationsfrei. 

C = gelten, was man durch kurze Rechnung bestätigt 

r Wirbelfaden von links 

die 

nach 

Zeichenebene 

rechts = Daumen 

hinein: 

⇥ 

⇤ 2⇥ 

⌃ Man kann diesen Satz hbeweisen, indem man für eine beliebige das infinitesimal kleine Fluidelement umschließ Wir 

u 

>> 

" 1 

C = w(z)dz Kurve, = idie eine 

⌅ln |z| infinitesimal +iarg(z) ⇧ 

kleine u’ = Fläche " 12 P P 

dA = einschließt . 

2 ⌥ ⌦ 2 r die Zirkulation " = ⇥ndA berechnet. Da über dieser 

infinitesimal kleinen= 

Fläche =0 ⇥ ⇤ const. und n ⇤ const ist gilt für die Zirkulation zu einem Zeitpunkt " 1 t 

2 

S 

x’ 

0 

also (t 0 )=0, wegen ⇥(t 0 )=0. u P Wegen 

u 

des Kelvinschen Wirbelsatzes bleibt diese Eigenschaft aber für alle 

Dipol 

P 

u ! senkrecht zur 

Zeiten erhalten undinduzierte somit h bleibt u ! 

Geschwindigkeit senkrecht für r daszur betre Zeichenebene ende Fluidelement ⇥ =0. 

uϑ in das Blatt hinein = Zeigefinger 

Eine weitere Elementarströmung kann man erzeugen, wenn man eine Senke in ⇥ und Füreine den Quelle Grenzfall in des ⇥ unendlich langen geraden 

u senkrecht zur 

superponiert und dann Für Der den 

II. Grenzfall 

Helmholtzsche des ⇥ ⇥ 

I’ 

unendlich 0 betrachtet: 

Wirbelsatz langenlautet: 

geraden Wirbelfadens ( 1 ⇥ 0, 2 ⇥ ⇥) ergibt sich : ! 

Für den unendlich langen geraden Wirbelfaden folgt aus α 1 =0 und α 2 =π : u = . 

"! 

Für den Grenzfall 2⇥r des unendlich langen geraden 

F (z) = Q Q 

ln(z Satz + u ⇥) 3= Fluidelemente, ln(z . ⇥) 

(1.11) 

Wirbelsätze 

2 

 

2⇥r die zu irgendeinem Zeitpunkt zu einer Wirbellinie gehören, bleiben für alle Zeiten 

⌥ ⌦ 

2 

⌥ ⌦ 

Reiht man unendlich viele dieser unendlich lange 

x 

Es wird vorausgesetzt, Reiht 

Quelle auf dieser man dass unendlich Wirbellinie. Senke 

die Strömung vieleD.h. dieser reibungsfrei 

Wirbellinien unendlichist, langen bewegen 

dass geraden auftretende 

sich Wirbelfäden mit dem 

Volumenkräfte 

Fluid, u 

mit sind = 

konstanter ein 

daher . 

Potential Wirbelstärke materielle 

haben 

1 Linien. 

Man spiegelt den Wirbel I mit entgegengesetzter Zirkulation auf die andere Seite der Wand der und x 1 -Achse erhält 2⇥r aneinander, so so erhält entlang und man die u 

einendass weiteren die Wirbel Strömung Iderbarotrop x 1 -Achseist. 

aneinander, so erhält man die unendlich ausgedehnten, Der Spezialfall ebenen Wirbelschicht eines langen, .Für jeden 

Der mit Beweis 

= Zirkulation Q dieses Satzes . I induziert erfolgt ebenfalls u P in P mittels u ⇥ des normal Kelvinschen zurReiht Wand, Wirbelsatzes, man weswegen 

2 ln z + ⇥ 

z ⇥ 

unendlichindem viele dieser man zunächst unendlich geraden zeigt, lange Wir 

die Normalenkomponente 

Kelvin daß 

der 

In eine 

überlagerten 

einer Fläche, reibungsfreien, die 

Geschwindigkeit 

jemalsbarotropen eine 

auf 

Wirbelfläche 

der Wand 

Strömung, war, 

verschwindet. 

deren dieseVolumenkraft Eigenschaft der ausgerichteten x 1 -Achse für eine alle aneinander, Zylinderkoordinatensystem 

Potentialkraft Zeiten beibehält. so erhält man 

ist, Dies die beha kannu 

Für ⇥ ⇥ 0 

manbleibt einsehen, die Zirkulation wenn manum dieeine Zirkulation geschlossene entlang materielle einer Kurve Kurve auf zeitlich dieserkonstant. 

Wirbelfläche berechnet, die also 

kleinen Fläche ⇥ ⇤ const. und n ⇤ const ist gilt für die Zirkulation zu einem Zeitpunkt t 0 

wegen ⇥(t 0 )=0. Wegen des Kelvinschen Wirbelsatzes bleibt diese Eigenschaft aber für alle 

und somit bleibt für das betre ende Fluidelement ⇥ =0. 

ltzsche Wirbelsatz lautet: 

mente, die zu irgendeinem Zeitpunkt zu einer Wirbellinie gehören, bleiben für alle Zeiten 

ellinie. D.h. Wirbellinien bewegen sich mit dem Fluid, sind daher materielle Linien. 

es Satzes erfolgt ebenfalls mittels des Kelvinschen Wirbelsatzes, indem man zunächst zeigt, 

, die jemals eine Wirbelfläche war, diese Eigenschaft für alle Zeiten beibehält. Dies kann 

wenn man die Zirkulation entlang einer Kurve auf dieser Wirbelfläche berechnet, die also 

uß. Wegen des Kelvinschen Wirbeltheorems muß dies für die Kurve auch zu späteren Zeidaher 

bleibt die Wirbelfläche eine Wirbelfläche. Anschließend argumentiert man, daß die 

F (z) = Q⇥ verschwinden muß. Wegen des Kelvinschen Wirbeltheorems muß dies für die Kurve auch zu späteren Zeiten 

gelten, und daher bleibt die Wirbelfläche eine Wirbelfläche. Anschließend argumentiert man, daß die 

Helmholtz I z . 

Rotationsfreie Fluidelemente bleiben für alle Zeiten rotationsfrei. 

1.3 Wirbeltransportgleichung 

Wäre nun Q beschränkt dann würden sich Quelle und Senke annihilieren und man erhielte keine besonders 

Helmholtz II Schnittlinie Fluidelemente, zweier Wirbelfächen die zu irgendeinem eine Wirbellinie Zeitpunkt ist zu und einer diese Wirbellinie daher für gehören, alle Zeiten bleiben einefür Wirbellinie alle Zeit bleibt. 

Die Bedeutunge 

interessante Strömung. 

der Navier-Stokes 

Wenn aber 

auf dieser Gleichungen 

Q ⌅ 1/⇥ erlaubt 

Wirbellinie. als Wirbellinien Transportgleichungen 

wird, dann ist lim Q⇥ 

sind materielle für 

beschränkt. 

denLinien Impuls 

Man 

und hat 

bezeichnet 

bewegen für die Wirbelstärke 

daher 

⇤ 0 sich mit dem Fluid. 

1 Wirbel-Strömungen M = 

die 

lim 

Wirbeltransportgleichung 

Q⇥ als Dipolmoment da die 

für 

Potentiallinien 

den Wirbelstärkevektor 

den Feldlinien 

⇤. Diese 

eines 

Gleichung 

elektrischen 

erhält 

Dipols 

man 

entsprechen. 

durch 

15 

⇤ 0 

Helmholtz III Der Die III. Zirkulation Helmholtzsche einer Wirbelröhre 

= ⇤ Wirbelsatz lautet: 

Bildung 

Man 

der 

kann 

Rotation 

dann für 

der 

das 

Impulsgleichung. 

komplexe Potential 

Für Strömungen 

des Dipols schreiben 

mit konstanter Dichte 

u · ds auch als Intensität der Wirbelröhre. Hierbei ist 

Satz 4 FürS 

eine Wirbelröhre bezeichnet man = ⇤ unter den Annahmen 

wobei s ein Kurvenparameter der Wirbellinie ist. Der Wirbelstreckungsterm ist von u · zentraler ds auch als Bedeutung Intensität für der Wirbelröhre. Hierbei ist 

F (z) = M S 

(2.15a) 

die1. Dynamik Inkompressible des Wirbelstärkefeldes zStrömung, S eine bezeichnet die ⇤ · Wirbelröhre ⇤u =0 insbesondere man auch umschließende bei als turbulenten Intensität Kurve. der Strömungen. Wirbelröhre. Für zwei beliebige Hierbei solcher ist S eine Kurven die Wirbelröhre S 1 und S 2 gilt 

⌅ 

umschließende Kurve. Für zwei beliebige solcher Kurven S1 und S2 

⌅ 

⌅ 

gilt 

woraus ⌅u die komplexe Geschwindigkeit 

⇥ 

2. äußeres > u 0 Kraftfeld · ds : . Streckung ist Potentialfeld 1 des = lokalen u f · = ds Wirbellinienelements 

= ⇤G 2 = u · ds . 

⌅s 

⌅u S 2 S 1 S ⇥ 

w(z) = dF 

2 

< 0 : dz Stauchung = M z 

Außerdem 2 (2.15b) 

des lokalen bleibt Wirbellinienelements 

die Intensität einer Wirbelröhre für alle Zeiten konstant. 

3. Dichte ⌅s konstant ⇥ = Außerdem const bleibt die Intensität einer Wirbelröhre für alle Zeiten konstant. 

folgt. ⌅u Verschiebt man den Ursprung nach z = z 0 gilt 

Wirbeltransportgleichung : Kippen des Wirbellinienelements 

⌅s 

 

lautetFür dieStrömungen Wirbeltransportgleichung 

eines 

M 

⇤ F (z) = inkompressiblen Fluides konstanter Dichte (Geschwindigkeit ist divergenzfrei!) (2.15c) auf die keine 

Für eine Volumenkräfte zweidimensionale außer (z Strömung zPotentialkräfte 0 ) in der (x einwirken, 1 ,x 2 )-Ebene gilt besitzt für die Wirbelstärke die Wirbelstärke die ⇤folgende nur nochTransportgleichung 

eine Komponente 

⌅⇤⇤ +(u 3 in x 

· ⇤)⇤ 3 -Richtung, die man dann einfach als ⇤ bezeichnet. Der Wirbelstreckungsterm (⇤ · ⇤)u 

=(⇤ · ⇤)u + ⇥⇤ y 

(1.12) 

verschwindet ⌅t Potentiallinie 

identisch und die zweidimensionale Wirbeltransportgleichung lautet 

Vereinfachung für 2-D Strömungen in kartesischen Koordinaten: 

Die Summe ⌅⇤ der Terme auf der linken Seite ist die materielle Ableitung der Wirbelstärke und wird auch 

mit D⇤/Dt ⌅t + u ⌅⇤ ⌅⇤ ⌅ 2 ⇥ 

⇤ 

1 + u 2 = + ⌅2 ⇤ 

w 

. (1.13) 

abgekürzt ⌅x 1 (siehe ⌅x 2 auch Vorlesung Strömungslehre I). Der erste Term auf der rechten Seite 

ier Wirbelfächen eine Wirbellinie ist und diese daher für alle Zeiten eine Wirbellinie bleibt. 

oltzsche Wirbelsatz lautet: 

e Wirbelröhre bezeichnet man 

elröhre umschließende Kurve. Für zwei beliebige solcher Kurven S 1 und S 2 gilt 

· ds = 2 = 

t die Intensität einer Wirbelröhre für alle Zeiten konstant. 

⌅x 2 1 

⌅x 2 2 

ist der sogenannte Wirbelstreckungsterm , der zweite +Q Term!Qauf der rechten Seite ist die Di usion von 

Für Strömungen mit nicht-konstanter Dichte kann man auf gleiche Art und Weise wie für Strömungen mit 

Wirbelstärke. 

x 

konstanter Dichte eine Transportgleichung für die spezifische Wirbelstärke ⇤/⇥ herleiten. Für den Fall einer 

reibungsfreien Mit der Zerlegung Strömung des Geschwindigkeitsvektors erhält man u in eine zur Wirbellinie und damit zu ⇤ parallele und in eine 

Stromlinie

ausgehende Reibungswiderstand kann so alleine natürlich nicht berücksichtigt und werden. Dieser Reibungswiderstand 

macht den Großteil des Gesamtwiderstandes aus, so z.B. ist der⇥ 

Anteil des ! Reibungswiderstandes 

⇥ 

⇧⌅⇤⌃ 

⇥x 

⇧⌅⇤⌃ 

⇥ ⇥y 

⇧⌅⇤⌃ ⇧⌅⇤⌃ 

⇥ 

0,h)=⇥ 

"=const 

für ein Verkehrsflugzeug im Reiseflug ca. 80%. 

!= const = ⇥ ⇥x 

+ ⇥ ⇥y=u 

A = 1 S 

= r sin =v =r cos 

2 Ch . ⌅⇥ 

f(z) = a n z n . 

= r( u sin + v cos )=ru 

⇥ 

⇧⌅⇤⌃ 

⇥x 

⇧⌅⇤⌃ 

⇥ ⇥y ⇥ 

n= ⌅ 

Damit ist für eine Neumann-Randbedingung Wegen ⇧⌅⇤⌃ der Orthogonalität ⇧⌅⇤⌃ 

" 

bekannt von Stromlinien und entlang unddeP 

: 

=u 

Potentialströmungen 

22 

= r sin 

! 

=v =r cos 

Laurent-Reihen 

⇤ 

sind eine Verallgemeinerung der aus der reellen bedingung Analysis bekannten gefordert werden. Potenz-Reihen. Die in der Vorlesung Strömungslehre I be 

2.1 Geschwindigkeitspotential 

!= const 

⇧ · ⇧⇥ =0 

Wegen der Orthogonalität von Stromlinien und Potentiallinien 

2.3.3 ⇥ A ⇥DieElementarströmungen 

xkomplexe Definitionen 2 = h 2 Integration + x 

2 1 . entspricht dem Wegintegral in zwei 2 Potentialströmungen 

Reibungse Raumdimensionen. ekt und kann 

" Wennvon man einer einerotationsfreien Funktion und daher reibungsfreie 

komplex Potentialfunktion 

integriert muß ! ein 

werden. 

exaktes Stromfunktion Integral der inkompressiblen Wird der Gradientenoperator Kontinuitätsgleichung dieser ⇤ Gleichung · u =0. 

In diesem Für eine Abschnitt rotationsfreie werden Strömung die28 man also zunächst den genauen Integrationsweg ⇧ · angeben. ⇧⇥ =0 Ist aber f(z) analytisch 

wichtigsten ist dieElementarströmungen Geschwindigkeit u der zur Gradient Beschreibung einer Potentialfunktion zweidimensionaler ⇥Po- 

tentialströmungen mittels 


auf Das einemGeschwindigkeitsfeld Gebiet A bis auf isolierte einer Singularitäten Potentialströmung (Punkte mitz, Stromfunktion Eine z = denen Wandkontur Inkompressible x + iy, f(z) i= ⇥ ⇧ nicht definiert ist 1, {F, 2-D definiert einer z} man Strömungen wird ⌅Potentialströmung C; die durch ist) Forderung {x, und y, : ⇤, sind tri ⇥} tvollständig ⌅ R. immer F (z) eine istdurch 

eine Stromlinie, analytischedaF 

u = ⇤⇥ u ( . ) des Superpositionsprinzips anhand ihrer komplexen 

= 

Wird eine der 

Darstellung 

Stromfunktion " Gradientenoperator 

besprochen. 

bzw. umläuft Ψ beschreibbar in 

⇥ 

dieser 

⇥⇥ (2.1) Gleichung in Polarkoordinaten au 

ist der Gradient einer Potentialfunktion Φ. Isolinien von man die ⇥ Forderung 

Wegen Φ, d.h. ⇤⇥ Linien ⇥ 0Φ ist = const, das Geschwindigkeitsfeld sind Potentiallinien. rotationsfrei. Eine Strömung y = u, ⇥ 

deren x = Geschwindigkeitsfeld 

v. ⇥r ⇥r + 1 ⇥ 1 ⇥⇥ 

=0 

r ⇥ r ⇥ 

(x 1 ,x 2 )= C der Integrationsweg S keine Singularität, dann eine ist immer zweidimensionale das tangential Integral wegunabhängig: 

Potentialströmung zur Wandoberfäche in dergerichtet komplexenist. Zahlenebene Daher kann dar. eine Da die Wand komp 

28 2 Potentialströmungen 

h x F (z) den, in z 

y zwas existiert, eine Möglichkeit muß dF/dz unahängig zur Darstellung vom Weg von derfesten Annährung Wänden, z + dz ohne ⇥ ztatsä 

sein 

Parallelströmung ⇤ 2x 1 + ⇤f 1 (x 2 ) , ⇤ 

⇤ b einmal dz = dx wählen und 

gemäß (2.1) aus einer skalaren Funktion berechnet werden kann, nennt 

⇥ 

Isolinien man 

⇥⇥ 

Aufgrund der Definitionen von Stromfunktion und von Potentialströmung Ψ, d.h. Linien . Ψ = const, sind Stromlinien. 

Für eine 

Inkompressible 

inkompressible 

Potentialströmungen 

Strömung folgt wegen 

genügen 

⇤ · u =0: 

einer Die Stromfunktion 

⇥r ⇥r 

Potentialfunktion + 1 erhält 

2 Potentialströmungen 2 Potentialströmungen zu begrenzen, bietet. ⇥ Da 1 ⇥⇥ jede Stromlinie ⇥⇥ 

=0 folgt ⇥ u 

r 

Die Differenz hat 

⇥ 

von folgene 

r ⇥ r 

Ψ1 und Eigenschaften: ⇥r + 27 eine u 1 Wand ⇥⇥ 

27 darstellen kann, mu 

28 f(z)dz = f(z)dz = f(z)dz = ···= f(z)dz = F (b) F (a) 

=0 

Bei einer Parallelströmung r ⇥ 

Ψ2 auf zwei Stromlinien S1 

(x 1 ,x 2 Laplacegleichung 

)= C 2 und S2 entspricht dem Volumenfluss pro Einheitsbreite 

Aufgrund ⇥ 

2 ⇥ 

2 ⇥ · ⇥⇥ = ⇤ ⇤⇥ 

⇥ = der Definitionen V21 zwischen diesen Stromlinien. 

x 2 + 

1 x 2 + von Stromfunktion ⇤x ⇤x 

2 x 2 =0. und + ⇤ ⇤⇥ 

= uv + uv =0, ⇥⇥ 

Potentialfunktion ⇤y ⇤y ⇥ u 

folgt r 

1. Linien ⇥(x, 

⇥r + u 1 ⇥⇥ Diese Gleichung ist erfüllt, wenn 

h x handelt es sich um eine konstante Strömung an dF z 2 Potentialströmungen 

y inder eine Stelle feste u einer Richtung, Wanddie eine also Stromlinie durch vorliegt. Das kann entweder dur 

S 

S 

1x 2 + 

1 S 

f 2 (x 1 ) . 

2 a 

parallele Geschwindigkeitsvektoren dargestellt wird. 

lungsprinzip, oder allgemeiner durch das Überlagern von Elementarström 

mit z mit = x z + = iy, x i= + iy, ⇧ i= 1, ⇧ dz = ⇥⇥ 

⇥x +i⇥⇤ ⇥x , 

{F, 1, z} {F, ⌅ C; z} ⌅{x, C; y, {x, ⇤, ⇥} y, ⇤, ⌅ ⇥} R. F ⌅(z) R. ist F (z) eine istanalytische einev 

oder =0 

besprochen Sman wählt dz =idyanalytische und erhält Funktion Funktion und stellt und stellt 

z 1 werden, y) erreicht =const 

r ⇥ werden. sind ⇥⇥Stromlinien: 

(2.2) 

eine zweidimensionale eine zweidimensionale 

3 

⇥ · ⇥⇥ = ⇤ ⇤⇥ und 

⇤x ⇤x + somit ⇤ ⇤⇥ bilden Potential- und Stromlinien Dieseorthogonale Gleichung ist Kurvenscharen. 

erfüllt, wenn ⇥r = u 

(x = uv + uv =0, 

1 ,x 2 )= C Potentialströmung Potentialströmung yin der in komplexen y der komplexen 

u 

Zahlenebene Zahlenebene dar. Da dar. dieDa komplexe die komplexe Ableitung Ableitung von von 

u 

dF 

F (z) in F (z) 

Zwischen ⇤y Potentialfunktion ⇤y und Stromfunktion gelten weiterhin 

Aufgrund Stromlinien der Definitionen sind immer vonorthogonal Stromfunktion zu und Potentiallinien, Potentialfunktion dies folgtaus d⇥ der =0Definition ⇥ dx| gemäß1Definition ⇥⇥ 

Stromlinie 

von Strom- = dy| die 

h x z existiert, in z existiert, 

1x 2 . muß dF/dz muß dF/dz unahängig unahängig vom Weg vom der WegAnnährung der Annährung v z + dzz + ⇥dz z sein. ⇥ z Man sein. x 

dz = 1 ⇥⇥ 

i ⇥y + ⇥⇤ 

⇥y = ⇥⇤ i ⇥⇥ 

⇥y ⇥y kann Man daher kann daher 

⇥⇥ 

Stromlinie 

w 

S 

einmal einmal dz = dx dz wählen = dx wählen und erhält und erhält 

u 

2 

und Potentialfunktion 

und somit bilden Potential- u 

v 

⇥ · ⇥⇥ ⇤ Cauchy-Riemann-Di und 

⇤⇥ 

⇤x ⇤x + ⇤ Stromlinien erentialgleichungen, orthogonale Kurvenscharen. die für ⇥r die = komplexen u 

= u r 

Da2.2 dF/dz u inBernoulli-Gleichung beiden Fällen gleich Beschreibung sein muß, r ⇥ müssen von für ⇥Potentialströmungen und ⇤ die Cauchy-Riemann-Di von e 

⇤⇥ 

Zwischen dF Potentialfunktion Bedeutung und = uv + uv =0, 

⇤y ⇤y Stromfunktion sind (siehe Abschnitt gelten weiterhin 2.3.2): 1 ⇥⇥ 

gemäß Definition = u r 

die 

Also besteht in Polarkoordinaten folgender Zusa 

Cauchy-Riemann-Di 2. Die Di erenz von ⇥ 

Aus obigen Definitionen 

erentialgleichungen, 

folgen ferner 

die 

die 

für 

Cauchy-Riemann 

die komplexen Beschreibung 

Differentialgleichungen 

von Potentialströmungen 1 und ⇥ 2 auf zwei von Stromlinien S 1 und S 2 entspric 

und somit bilden Potential- und u = Stromlinien ⇤ orthogonale Kurvenscharen. 

Bedeutung kartesische sind (siehe Koordinaten Abschnitt 2.3.2): ⇤x = ⇤⇥ 

r ⇥ 

(2.5a) 

⇤y 

Also 

Polarkoordinaten 

diesen besteht Stromlinien Polarkoordinaten u r = ⇥ : folgender ⇥r = 1 ⇥⇥ 

1) =⇥(0,h) ⇥(0, 0) = 1 Bereits in der Vorlesung 

b 

dz = dF ⇥⇥ 

dz ⇥x = +i⇥⇤ 

⇥⇥ Man kann w auch darstellen in Polarkoordinaten : 

⇥x ⇥x +i⇥⇤ , ⇥x , 

v 

x 

(2.5) erfüllen. Aus diesen folgt wiederum: 

Strömungslehre I wurde die Bernoulli-Gleichung 

rZusammenhang ⇥ 

zwischen Po 

Zwischen Potentialfunktion 2 Ch . 

u 

Man kann w auchw darstellen =(u r iuin ⇥ )e Polarkoordinaten i⇥ ⇥ 

chung : 

2 ⇥ 

x 

Sentlang einer ausgezeichneten Kurve besprochen. Es wurde gefunde 

oder man oderwählt man wählt dz =idy dz =idy und 

und 

erhält und erhält 

⇥x 2 = ⇥2 ⇤ 

x3 

⇥y⇥x = 

⇥2 ⇥ 

⇥y 2 ⇤ ⇥ =0 

Stromfunktion gelten weiterhin gemäß Definition die 

Cauchy-Riemann-Di erentialgleichungen, die für die komplexen Beschreibung von Potentialströmungen 2 

u = ⇤ von 

Bedeutung sind 

⇤x ⇤⇥ v ⇤ (2.5a) 

(siehe 

⇤y 

⇤y = ⇤⇥ 

der Impulsgleichung 

u r = ⇥ (2.5b) 

⇤x 

⇥r = 1 für eine reibungsfreie 

⇥⇥ 

u = 1 Strömung 

⇥ 

Strömungsrichtung teste u in A: u = ⇥⇥ mit einem Potential fü 

Man kann dF 

a 1 > 0, u 2 =0, unter der Bedingung, r daß ⇥ man entweder 

r ⇥ 

entlang 

⇥r 

einer Stromlinie integrie 

dz = wdF 

1 ⇥⇥ 

i ⇥y + ⇥⇤ 

Abschnitt = ⇥⇤ i ⇥⇥ 

dz = darstellen 1 w ⇥⇥ =(u 

i ⇥y + r ⇥⇤ in 

iu 

Polarkoordinaten 

⇥y ⇥y 

= ⇥ )e ⇥⇤ i⇥ i ⇥⇥ 

⇥ 

: 

2 ⇤ 

z=r e i! 

y 

⇥y 

2.3.2): ⇥y ⇥y ⇥y 

2 = ⇥2 ⇥ 

⇥x⇥y ˙V = 

⇥2 ⇤ 

⇥x 

ab = d⇥ 2 ⇤ ⇤ =0 

schwindigkeitsfeldes, = ⇥ 2 ⇥ 1 . 

1 

v = 

u ⇤ ⇤ ⇤y für Fluide mit konstanter Dichte 

Stationär, ⇤x = ⇤⇥ ⇤⇥ 

u = 1 ⇥ 

also 

= ⇥⇥ die Wirbelstärke, identisch verschwindet. Man er 

Umläuft oder tri t ein (2.5b) 

⇤x 

Oft 

geschlossener 

ist eine Darstellung 

Integrationsweg 

von Potential- 

S, der ganz im letzteren in 

Stromfunktion 

A liegt, Fall r ⇥ 

Singularitäten, mitineiner Polarkoordinaten ⇥r 2.3.1 auf dem so ist Wichtige 

(2.5a) zweckmäßig: Fakten aus der kom 

, ist die DaBernoulli-Gleichung dF/dz 

w Da=(u dF/dz in r beiden 

iu in ⇥ beiden )e 

Fällen i⇥ ⇥ und ⇤ erfüllen also 

z=r e 

mit Fällen gleich derselben gleich sein muß, sein Konstante müssen muß, müssen ⇥ und⇥ ⇤und die ⇤Cauchy-Riemann-Di die i! jeweils die Laplace Gleichung. In der reellen zweidimensionalen 

y 

ganzen Gebiet gültigen Konstante. 

unter ⇤y Verwendung des 

y Unter 

Dies gilt 

Verwendung 

für eine 2D 

einer 

Konfiguration 

zeitabhängigen 

Die komplexe Geschwindigkeit 

1 

mit Einheitsbreite in der x 3 Koord 

Geschwindigkeitsbetrages q und des Druckes p 

Potentialfunktion Φ(t) und der Bernoullikonstanten F(t) 

Oft ist v = eine ⇤ Darstellung man für den Volumenfluß dann b ˙V 21 . 

⇤y = ⇤⇥ 

läßt sich daher leicht angeben als 

Für ein Fluid konstanter 

Eine 

Dichte 

komplexe 

erhält man 

Zahl 

die 

z = 

Bernoulli-Gleichung 

x+iy repräsentiert 

für 

einen 

Po 

f(z)df = ⇥ Potentialströmungen u ist ⇥ =0eine erentialgleichungen 

erentialgleichungen 

Folge der Divergenzfreiheit der Geschwindigkeit, 

u ! 

(2.5) erfüllen. (2.5) erfüllen. Aus diesen Aus diesen folgt 

⇥ S (p)Resf(z 

wiederum: folgt wiederum: 

ne Folge der Rotationsfreiheit der Geschwindigkeit. In der komplexen Betrachtung stel 

p ) . 

2⇤i 

z=r e2.3.1 Wichtige Fakten aus der komplexen Analysis: 

von Potential- und Stromfunktion in Polarkoordinaten i! 

r 

u 

komplexen Potentials r 

zweckmäßig: daß die imaginäre (2.5b) Einheit i= ⌅ 1 die zweite Ko 

+ qw(z) 2 ⇤x 

2 

A = p =U + qiV ⇥ 

. 

const . 2 y 

Eine komplexe Zahl z = können x+iy(2.12a) 

⇥t + 1 F (z) die Potentialfunktion 

2 ⇥⇤ ⇥2 + p und der Imaginärteil die Stromfunktio 

p 

S 

⇥ 2 ⇥ 

+ G 

repräsentiert 

= F (t) 

einen Vektor mit den Kompon 

q 2 = w 2 = u 2 + v 2 

daß die imaginäre Einheit i= y 

⌅ der reellen Analysis entsprechende Opera 

Hierin⇥x ist 2 = ⇥ 2 ⇥ ⇥2 ⇤ 

p der ⇥y⇥x Index = 

⇥2 ⇥ 

⇤ ⇥ =0 (2.9a) 

⇥x 2 = ⇥2 ⇤ 

⇥y⇥x der ⇥y = 

⇥2 y 

u 

! 

⇥ 

2 

Singularität ⇥y 2 ⇤ in ⇥ =0 Strömung dar. u ! 

A, ⇥ S (p) die Umlaufzahl dieser Singularität und Resf(z p ) das 

(2.9a) 

r 

x 

In der u 

wird als C 1= die {x zweite +iy|x, Komponente y ⇤ R} , i = des ⌅ r 

komplexen Beschreibung definiert man eine komplexe Geschwindigkeit als kompl 

Vektors 1, bez 

Oft ist eine Darstellung von Potential- und Stromfunktion in Polarkoordinaten u zweckmäßig: 

x 

Daraus 2 u 

1) undResiduum folgt 

damit 

das komplexe von f in zPotential p . durch Bildung der Stammfunktion F (z) Diese nach (wobei Gleichung z: die beliebige hat folgende Integrationskonstante 

hier 2 ⇤ 

Eigenschaften: 

⇥ können der reellen Analysis entsprechende Operationen definiert werden 

y 

Man kann eine Stro 

wird als C u r 

r 

{x +iy|x, y ⇤ R} , i = ⌅ komplexe Zahl in kartesischen Ko 

zu Null gesetzt wurde) 

⇥y ⇥ 

1, bezeichnet. 

+ C 2 x 2 = ⇥ 2 ! 

⇤ ⇥2 ⇥ 

1Komplexe 2 ⇥x⇥y = 

⇥2 ⇤ 

⇤ =0 (2.9b) 

⇥y 

2 + 2 = ⇥2 ⇥ 

x 2 ⇥x⇥y ⇥x = 

⇥2 u 

⇤ 

! 

oder durch den 

⇤ 

Geschwindigkeitsbetrag 

⇤ =0 

q = |w| = | ¯w| und xden vom Geschwindigkeitsvektor 

(2.9b) 

mit der reellen 

r 

2 ⇥x2 u 

Aches eingeschlossenen Winkel 

r 

: w(z) 1. sie = gilt dF 

im gesamten Strömungsgebiet mit derselben (möglicherweise z 

2.3.2 Komplexe 1 Darstellung . 

Darstellung 

für 2D 

zweidimensionaler ! 

Potentialströmungen u 

Potentialströmungen 

dz = ⇥⇥ 

⇥x +i⇥⇤ ⇥x = u iv =(u r iu ⇥ )e i⇥ = qe i , 

u 

" 

x b 

! Man kann eine komplexe Zahl kartesischen Koordinaten oder in Polar 

€ 2 ⇥F (z) und=(U ⇥⇤und erfüllen ⇤ 

hoder 2 iV )z erfüllen durch also . jeweils also den Geschwindigkeitsbetrag jeweils die Laplace die Laplace Gleichung. Gleichung. q = In |w| derIn = reellen | der ¯w| und F reellen (t), zweidimensionalen zweidimensionalen Betrachtung (2.12b) Betrachtung von von 

x den vom Geschwindigkeitsvektor 

! = ! 

mit der reellen 

r 

2 

NachPotentialströmungen im 2 vorigen Aches Abschnitt eingeschlossenen ist ⇥ ist angegebenen =0eine w ⇥ = =0eine qeWinkel i 

mit z = re i⇥ , q = |w|, = atan(v/u). 

Folge Satz Folge über der : uDivergenzfreiheit die ! 

n 

rder komplexe Divergenzfreiheit erenzierbarkeit der Geschwindigkeit, der Geschwindigkeit, existiertund ein komplexes und ⇤ =0eine 

Folge Folge der Rotationsfreiheit der Rotationsfreiheit der Geschwindigkeit. der Geschwindigkeit. In derInkomplexen komplexen Betrachtung Betrachtung Zusammenhang 

⇤ =0ei- 

Potential27 

Da F (z) keine 

Komplexes 

Singularitäten 

Potential 

aufweist verschwindet 

u! 

" 

die u komplexe Zirkulation 2. sie identisch gibt einen: 

stellt der stellt y 

Realteil 

zwischen Druck p und Potentialfunkt 

oder durch xdes 

dy 

F (z) 

den 

x ! 

u 

1 )=p A C 2 = x2 Geschwindigkeitsbetrag 

1 

u r 

h . (x, y)+i⇥(x, y) 

q = |w| = | ¯w| und den vom Geschwindigkeitsvektor mit der 

der 

reellen 

Realteil des 

⇤ berechnet werden, 

(2.8) 

Aches komplexen komplexen Potentials 

C =0eingeschlossenen Potentials 2 w F = Winkel (z) qe die F i 

y 

(z) Potentialfunktion die Potentialfunktion und der undImaginärteil der Imaginärteil die Stromfunktion die Stromfunktion der zugehörigen der u 

r 

mit z = x + iy, Die i 2 : 

zugehörigen 

w=u+iv 

Geschwindigkeitskomponente = 1, {F, z} 2 C; {x, y, in, radialer } 2 R. Richtung F (z) istwird eineaus analytische den kartesischen V dx 

ab 

FunktionKomponenten und stellt 

Strömung Strömung dar. dar. 

gemäß folgender 

Potentialströmung Vorschrift berechnetin der komplexen Zahlenebene dar. Da die komplexe Ableitung 1 und p 2 zweier 

u! 

" 

3. da (2.3) nichtlinear x 

eine zweidimensionale 

ist, sind aber die Druckanteile p 

In der Komplexe w Inkomplexen = der qekomplexen i 

y 

v 

u 


Beschreibung Beschreibung 

⇥ definiert definiert man eine man komplexe eine 

! 

komplexe Geschwindigkeit Geschwindigkeit als komplexe als komplexe Ableitung Ableitung von von 

Die ist Geschwindigkeitskomponente definiert als die komplexe inAbleitung radialer Richtung von F(z) nach wird aus z den kartesischen Komponenten gemäß folgender 

2 einmal Vorschrift dz h 2 = berechnet dx wählen und erhält y 

u 

p A + C 2 von F (z) 2x 2 z existiert, muß dF/dz unahängig vom Weg der 

im 

Annährung 

allgemeinen 

z 

nicht 

+ dz ! 

superponierbar ! 

z sein. Man 

p 

kann 

= p 1 

daher 

+ p 2 . 

F (z) nach F (z) z: nach z: 

q ! 

1 

1 . u r = q cos(⇥ )=q(cos ⇥ cos + sin ⇥ sin ) = cos u + sin v, 

x 

a 

w(z) = w(z) dF = die Geschwindigkeitskomponente in Umfangsrichtung gemäß 

Die Geschwindigkeitskomponente u r = qdF 

cos(⇥ dz dF ⇥⇥ 

)=q(cos ⇥incos radialer + sinRichtung ⇥ ) = wird cosaus u 2.3 den + sinkartesischen Zweidimensionale, v, Komponenten gemäß inkompressible folgender 

Vorschrift dz = @ ⇥x +i⇥⇤ 

! = ! 1 Potent 

berechnet @x +i@ ⇥x = u iv =(u 

@x u = , 

r iu ⇥ )e i⇥ = qe i , (2.10) 

dz = ⇥⇥ 

"! 

x 

⇥x +i⇥⇤ ⇥x = u iv =(u r iu ⇥ q)e i⇥ = ! qe i , x (2.10) 

u 

q sin(⇥ )= sin u + cos v. 

w=u!iv 

mit die z Geschwindigkeitskomponente 

mit = rez i⇥ = , q re= i⇥ |w|, , q = |w|, Die = atan(v/u). komplexe = atan(v/u). 

in Umfangsrichtung Zirkulation wirdgemäß 

folgendermaßen Zur Vereinfachung berechnet wird : 

q ! 

x für zweidimensionale Strömung folgende Nomenk 

Man u 

oder 

r = beachte, q 

man 

cos(⇥ 

wählt 

dass )=q(cos 

dz =idy 

in der ⇥vektoriellen cos 

und erhält 

⇥ 

+ sin Darstellung ⇥ sin ) = cosdie u komplexe + sin v, Geschwindigkeit dem an der x-Achse gespiegelten 

Geschwindigkeitsvektor 

u = q sin(⇥ )= sin 

entspricht. 

u + cos y v. y ⇥ Man beachte, daß der vektoriellen Darstellung die komplexe Geschwindigkeit gerade de 

Linienx⇥ 1 = const x, xsind 2 = y, also udefinitionsgemäß 1 = u, u 2 = v, Stromlinien. ⇥u⇥ 2 = u 2 Linien + v 2 = mit q 2 konst . 

die Geschwindigkeitskomponente 

dF Die 

in Umfangsrichtung gemäß const bezeichnet man als Potentiallinien : 

dz = komplexe 1 @ 

i @y + Zirkulation @ C 

@y = = @ wird w(z)dz 

i @ folgendermaßen = (u iv)(dx gespiegelten berechnet +idy) Geschwindigkeitsvektor 

x : 

enspricht. Daher ist das konjugiert Komplexe ¯w = u+ 

@y u u des physikalischen Geschwindigkeitsvektors in der komplexen Ebene z . 

S @y S 

Komplexe Zirkulation ⇥ ⇥ ⇥ w=u+iv ⇥ w=u+iv 

Die 

u = 

Komplexe 

q sin(⇥ 

Zirkulation 

)= sin 

ist 

u 

analog 

+ cos 

zum 

v. 

Eine zweidimensionale inkompressible Strömung (nicht nur Potentialström 

Die komplexe Realraum als Linienintegral der komplexen Geschwindigkeit definiert. Sie 

Da dF/dz Zirkulation in beiden 

C = wirdFällen w(z)dz folgendermaßen gleich 

= (udx sein+ berechnet iv)(dx 

muß, vdy)+i müssen 

+idy) : (udy 

v v eine und vdx) 

(2.11) 

skalare 

setzt sich aus der realen Zirkulation Γ und den von der Kurve d die 

S eingeschlossenen =0Funktion, Cauchy-Riemann-Di↵erentialgleichungen 

⇥ dx die+ 

Stromfunktion 

x Quellstärke dy =0 , beschrieben werden. Die Str 

S 

S 

Q zusammen 

S 

S 

⌅⇤⇥⇧ y 

(2.5) ⇥erfüllen. Aus diesen ⇥ folgt wiederum: ⇥ ! ! 

⌅⇤⇥⇧ 

=u =v 

C = w(z)dz = (u(udx iv)(dx + vdy)+i +idy) (udy vdx) = +iQ 

(2.11) 

@ 2 

⇥ dx v = dy 

S 

@x 2 = @2 SS 

⇥ 

@y@x = ⇥ 

@2 

S 

) =0 "! "! 

x x 

@y2 u (2.9a) 

Hierin ist = 

(udx + vdy)+i (udy vdx) 

(udx + vdy) = +iQ 

gemäss (1.3) die relle (physikalische) Zirkulation. (2.11) 

Q = (udy vdx) = 

S 

S 

S 

@ 2 (n x u + 

@y 2 = @2 S 

n y v)ds = u · nds ist der Volumenstrom durch die Kurve S, der aus den von S eingeschlossenen 

S 

Hierin ist = 

@x@y = (udx @2 

) =0 w=u!iv w=u!iv 

(2.9b) 

@x + 2 = vdy) S 

+iQ 

gemäss (1.3) die relle (physikalische) Zirkulation. Q = (udy vdx) = 

Quellen resultiert. 

S 

S 

(n x u + n y v)ds = u · nds ist der Volumenstrom durch die Kurve S, der aus den von S eingeschlossenen 

Man beachte, Manund 

beachte, Sdaßerfüllen indaß derin vektoriellen also der vektoriellen jeweils S Darstellung die Darstellung Laplace die Gleichung. komplexe die komplexe Geschwindigkeit In der Geschwindigkeit reellen gerade zweidimensionalen gerade dem an dem deran x-Achse Betrachtung der x-Achse von 

Hierin ist = 

Quellen 

(udx 

resultiert. 

+ vdy) gemäss (1.3) die relle (physikalische) Zirkulation. Q = (udy vdx) = 

gespiegelten gespiegelten Potentialströmungen S Geschwindigkeitsvektor ist enspricht. =0eine enspricht. Daher Folge Daher istder dasDivergenzfreiheit ist konjugiert konjugiert Komplexe Komplexe der ¯w Geschwindigkeit, = u+iv ¯w = S u+iv die Darstellung die und Darstellung =0eine 

physikalischen Folge der S Rotationsfreiheit Geschwindigkeitsvektors der Geschwindigkeit. der komplexen der komplexen Ebene In der Ebene z komplexen . z . Betrachtung stellt der Realteil des 

(n x u + n y v)ds = u · nds ist der Volumenstrom durch die Kurve S, der aus den von S eingeschlossenen 

Sdes physikalischen des 

Quellen resultiert. 

komplexen Potentials F (z) die Potentialfunktion und der Imaginärteil die Stromfunktion der zugehörigen

mitDie der u r komplexe Definition = , Geschwindigkeit u der=0. 

komplexen läßt Zirkulation sich daher leicht w angebenw 

als 

ngen 

werden und 2⇥r es liegt daher wieder eine Singularität im UrsprungPotentiallinie 

vor. 

u 

30 ⇥ 

30 

2 Poten 

w 

wichtigsten Elementarströmungen zur Beschreibung zweidimensionaler Daher Dieerhält komplexe C 

w(z) 

= 

Po-mauperpositionsprinzips anhand ihrer komplexen Darstellung besprochen. S 

=U 

w(z)dz Geschwindigkeit die komplexe iV 

= Q = const Geschwindigkeit läßt . sich daheraus 

leicht y angeben als 

Q ist die Quellenstärke,für Q>0 spricht 2⇥ (ln man |z| von +iarg(z)) =i Q 2⇥ =iQ, 

einer Quelle S für 2⇥ Q 0 bedeutet auch daher der Umlauf 

eine Grund im 

Singularität für math. diepos. eingangs Sinn, 

digkeit 

Einen Potentialwirbel 

leicht Polarkoordinaten 

kann auf. man erwähnte erzeugen, 

y 

Da F (z) F (z) keine =(USingularitäten iV )z . 

2⇥r sin Normierung 

angeben (der daher indem um 2⇥ ersichtlich wird. 


Quotient eine manSingularität die 

2⇥ 

Geschwindigkeitsvektoren S 

wird inauf. 

Kürze klar werden) 

der Qu 

utet Umlauf im math. neg. Sinn. Gemäß Definition der komplexen Zirkulation muß für den 

Stromlinie 

kenströmung um 90 dreht. Wiederum aufweist kann verschwindet daher im die komplexe Zirkulation identisch : 

Die Stromlinien Die Stromlinien sind o ensichtlich sind o ensichtlich vom Ursprung vom Ursprung ausgehende ausgehende Strahlen, Strahlen, Potentiallinien Potentiallinien sind konzentr sind 

als Zirkulation 

w Kreise um 

römung 

Kreise den 

u 

DaUrsprung. F um r = 

Q 

yUrsprung keine eindeutige Geschwindi 

bel C = gelten, was man durch kurze Rechnung bestätigt 

Potentialwirbel 

Stromlinie 

⇥ 

⇤ 

werden und es liegt 

(z) den 2⇥r keine Singularitäten aufweist verschwindet die komplexe Zirkulation identisch : 

Die komplexe C =0 Ursprung. Wird , u daher 

eine =0. wieder eine Singularität im Ursprung vor. 

2⇥ 

⌃ 

Geschwindigkeit läßt sich daher leicht angeben als 

⇥ 


w = u iv = Q 

Wird Quell- eine oder Quell- Senkensträrke oder Q ist Senkensträrke die Quellenstärke,für Q vorgegeben, Q vorgegeben, soQ>0 kann spricht man so kann dieman Gesc man vo 

Einen Potentialwirbel kann man erzeugen, 

strömung ist charakterisiert durch eine radiale Anordnung von C =0 

2⇥r e i indem man die Geschwindigkeitsvektoren y 

w(z)dz = i ⌅ln |z| +iarg(z) ⇧ = digkeit 2 = leicht . 

w der Quellen- ode 

2 ⌥ ⌦ 2 digkeit in Polarkoordinaten leicht Polarkoordinaten angeben (der angeben Quotient (der 2⇥ Quotient wird 2⇥Kürze wirdklar in Kürze werden) klar werden) 

Daher erhält man die komplexe Geschwindigkeit mit der ausDefinition der 

kenströmung In Polarkoordinaten um 90 dreht. Geschwindigkeitsnabhängig 

von der Umfangskoordinate ist. Im Ursprung weist Wiederum 

w(z) =U iV = const . 

x 

u 

2⇥rdiese 2 re i Strömung = Q 

2⇥z¯z ¯z 

r = 

Q 

r = 

Q 

kann mankann die Geschwindigkeit daher im Ursprung wieder keineleicht eindeutige 

Potentiallinie 

komplexen Zirkulation 

S 

= =0 

angeben, Geschwindigkeit wenn die Zirkulatio ange 

2.3.3 Elementarströmungen 

⇥ 

2⇥r u , = u =0. , u =0. 

r cos u sin 

uf. 

Daraus folgt das komplexe Potential durch Bildung der Stammfunktion (wobei die beli 

Quellen- und Senkenströmung 

Q ist die Quellenstärke, = Q 

= Q 

w 

werden und wird es : liegt daher wieder eine Singularität 31 

für Q > 0 spricht man von einer Quelle 

konstante für Q hier < 0 zu von Null einer gesetzt 2⇥z . 

2⇥r cos im Ursprung vor. 

C = w(z)dz = Q 20 2⇥ (ln |z| +iarg(z)) 2 Potential 

In diesem Abschnitt werden die wichtigsten y Elementarströmungen zur x Beschreibung zweS 

S 

Elementarströmung kann man erzeugen, wenn Daher man eine erhält Senke 

Daher tentialströmungen man inu erhält r ⇥die =0, undkomplexe man 

eineu die 

= 

komplexe mittels Geschwindigkeit . ⇥ 


Senke. wurde) 

aus 

und 

2⇥r 

des Superpositionsprinzips aus Potentiallinie 


woraus auch 

anhand 

der Grund 

ihrer 

für 

komplexen 

die eingangs 

Darstellung 

erwähn 

für undQ>0 dann den spricht Grenzfall man⇥ ⇥von0 betrachtet: einer y Quelle für Q0 spricht man 

und 

S 

2⇥ als von Ursprung Da Bei 

Qeiner ist F einer (z) keine Parallelströmung Singularitäten aufweist verschwindet die komplexe Zirkulation identisch : 

. ⇥ 

die 

(2.12a) F (z) 

Quellenstärke,für z 

= Q = 0: handelt es sich 

ln 

Q0 einer Senke. spricht 

Einen um eine 

Dies man ist von 

Potentialwirbel konstante 

konsistent einer Quelle 

x 

Strömung 

für 

kann 

Q0: (2.12b) 

2⇥r 

woraus auch der Grund für die eingangs erwähnte ⇥ w = woraus uNormierung F ⇥(z) iv w auch = u Q der ln(z um 

iv Grund = 

2⇥ z Q ersichtlich 

0) für . die eingangs wird. erwähnte Normierung um 2⇥ ersichtlich wird. 

ufweist verschwindet die komplexe Zirkulation identisch : 

2⇥r e i 

2⇥r e i = Q 

2 y i 2⇥r 2 x 

ann man erzeugen, indem man die Geschwindigkeitsvektoren u 

2⇥z . 

u r = 

Q 

r = 

Q r 

F =0, (z) Quelle = 

der 2⇥r Quellen- oder Senreht. 

Wiederum kann daher im Ursprung keine eindeutige 

= , u Q , 

i u =0. 

w 

2⇥ 

= ln(z z . 0) . 

gen 

beschränkt dann würden sich Quelle und Senke In annihilieren Polarkoordinaten undQ0: Potentialwirbel Quelle Dipols, 

entsprechen. 

Zentrum 

= i 

z=0 mit der Zirkulation Γ. 

u r =0, 2⇥z 

funktion Im bisUrsprung auf eine liegt eine Singularität vor. 

. Wird Einen eine Quell- Potentialwirbel oder Senkensträrke kann 

y 


u = u r cos. 

man Qerzeugen, vorgegeben, indemso Einen man kannPotentialwirbel dieman Geschwindigkeitsvektoren die Q u sin 

irrelevante 

Geschwinrdinatekenströmung 

angeben (der umQuotient 90 dreht. 2⇥Wiederum wird in Kürze kannklar daher werden) kenströmung im Ursprung umkeine 90 eindeutige dreht. Wiederum Geschwindigkeit kann daher angegeben 

= kann Q = 

man erzeugen, der Quellen- indem oder man Sen- 

die Geschwindigkeitsvektoren der 

2⇥z . 2⇥z . Integrationskonstante als 

Das Vorzeichen der Zirkulation bestimmt den Umlaufsinn und durch u 

: 

= uBildung u = u r cos u sin = Q 

r 2⇥r 

> 

cos 

0 bedeutet der u Stammfunktion sin bis auf eine irrelevante Integrationskonstante 

⇥ F (z) = Q Umlauf 

= Q 2⇥r 

2⇥rim cos 

2 

w(z) = 

i 

y 

x 

ann für das komplexe Potential des Dipols schreiben Q0 

Quelle eine 

mit 

spricht 

(Senke) Ursprung 

Singularität und man 

mit 

von 

Ursprung in 

einer 

z 

im 

=0folgt 

Ursprung Quelle 

in z 

für 

=0folgt nach 

vor. Q 

C 

0 = . gelten, was man durch u kurze = ufindet r Rechnung cos 

0. 

funktion bis 

Wenn 

funktion auf⇥ man w(z) 

der 

eine y bis udie bestätigt sin 

Ursprung 

irrelevante auf komplexe 

eine i 

= irrelevante 

z 

Integrationskonstante z. 


F (z) = 

i 

2⇥r 

2 

mit der Definition 2⇥z y 

der = komplexen z 

Integrationskonstante als als 

0 und nicht Zirkulation in z =0liegt, kann y 

⇥ 

⇤ 

ln(z) . . (2.16a) 

omplexe Geschwindigkeit 

man das komplexe Potential durc 

2⇥ 

⌃ 

v = 

Abbildung 

Zirkulation Potentiallinie 


mplexe Geschwindigkeit aus 

⇥ F (z) ⇥ Q u 

bestimmen 

F (z) ln z. Q v = u 

als 

r sin + u cos = Q 

r sin 

Ein Potentialwirbel 

⇥ 

+ u cos = Q 

t, dF stellt sie irgendeine Potentialströmung dar, deren mit Ursprung in z = z 2⇥r sin 

x 

0 kann wieder leicht durch eine Koordinatentra 

ln z. 

(2 

stimmt 2⇥ 

C werden 

ww(z)dz = Q 2⇥r sin 

v = u 

komplexe Ursprung 

2⇥ w 


bzw. in Polarkoordinaten 

in = Q 

Stromlinie 

F (z) = Q 2⇥ (ln |z| +iarg(z)) =i Q C = w(z)dz = i ⌅ln |z| +iarg(z) ⇧ r ⇥ w 

sin + 


= u uz cos = iv 0: 

= z= = 2 = . 2⇥r 

2 2⇥r x 2 y i 2⇥r 2 x 

0 : 

dz = M z 2 (2.15b) 

Die komplexe Geschwindigkeit In Polarkoordinaten 2⇥ =iQ, kann man die Geschwindigke 

2 ⌥ ⌦ als 2 

S 

2⇥r cos 

Wenn derWenn Ursprung der in Ursprung z 2⇥ = z ln(z 0 und in z nicht z als 

S 

2⇥ 

S 

findet man die komplexe Geschwindigkeit 

i 

= =0 

2⇥r 

2 (x 0) . 

iy) = i ¯z 

(z) läßt sich daher leicht angeben als 

F (z) = i iebt ln(z) wird : 

. z 0) . 

z = man nCzn den 1 Ursprung = nCr n nach 1 ez i(n = z 1) 0 gilt 

(2.16b) 


F (z) i ln(z zz 0 und in z nicht =0liegt, in z =0liegt, kann mankann das komplexe man das komplexe Potential durch Potential einedurc 

woraus auch der 0 ) . 

⇥ w u 

Abbildung Abbildung bestimmen bestimmen als 2⇥ iv Grund = Q 

2⇥z¯z 

M 


z) = 

⇥ w = 

Ursprung 

u> 0: iv Umlauf = 

in z = imz für die eingangs erwähnte Normierung um 

als 

⇥ w = u iv Q 2⇥ 

x 

2⇥r e ersichtlich i wird. 

Dipol 

2⇥r e i 

2⇥r 

2 y 0 mathematisch :(2.15c) 

i 2⇥r 2 x = positiven i Sinn u r =0, , 

ten erhält 

u = . 

(z zman 0 ) durch Vergleich mit der Transformationsbeziehung für die 2⇥z 

2⇥r 

x 

Daraus < 0: 

Eine weitere Potentialwirbel 

Dipol Elementarströmung kann man erzeugen, M ist das 

Stromlinie 

Dipolmoment 

Stromlinie 

os = Q 

F (z) = 

wenn Q F Umlauf (z) folgt 

= i 

F (z) = Q 

2⇥r sin 

2⇥ ln(z z 0) . 

2⇥ ln(z = Q 

man 2⇥r z eine 

0) . 

Senke in ⇥ und eine Quelle in = ⇥ 

Q 

2⇥r 2 re i = Q 

2 re i Q 

2⇥z¯z ¯z 

2⇥r 

2 (x = das im i Geschwindigkeit 

iy) 

komplexe mathematisch = i ¯z Potential negativen durch Bildung Sinn. der Stammfunktion (wobei die beli 

und durch Bildung2⇥ der ln(z Stammfunktion z 0) . 

bis auf Mittels eine Transformation irrelevante Integrationskonstante auf kartesische 

2⇥z¯z 

2⇥z¯z ¯z Koordina das kom (2 

)e i 

y 



konstante 

Keilströmung 

hier zu Null gesetzt wurde) 

(2 

superponiert 

n man die Geschwindigkeit 

und dann den 

wieder 

Grenzfall 

leicht 

⇥ ⇥ 

angeben, 

0 betrachtet: 

wenn 4. desDipol: 

die Potentialwirbels > 0: Zirkulation Umlauf immit vorgegeben mathematisch Ursprung 

Einen Potentialwirbel = kann Q in 

i man erzeugen, indem man die Geschwindigkeitsvektoren 

Potential 

= Q 

2⇥z . 

der 

kenströmung um 90 dreht. Wiederum kann daher im Ursprung keine eindeutige Geschwin 

⇥r . F (z) = Q 2⇥z . 

positiven z =0 Sinn , 

u = u r cos u sin = 

2⇥z 

2⇥r 

2 y 

w Ursprung 

Betrachten 

in z = 

zunächst 

0: 

unmotiviert die folgende Funktion 

< 0: 

Q 

⇥F Umlauf (z) (z) =(Uim mathematisch 

= i iV ln)z z. . negativen Sinn. 

Keilströmung 

ln(z + ⇥) ln(z ⇥) und durch 

2 

⌥ ⌦ 

2 Das 

Bildung 

⌥ ⌦ 

werden komplexe 

der Stammfunktion 2⇥ und 

= Potential M es liegt daher dieser 

bis 

wieder Quelle 

auf eine 

eine (Senke) 

irrelevante 

Singularität Das 

mit 

komplexe 

Ursprung 

Integrationskonstante 

im Ursprung Potential 

in z =0folgt 

das 

vor. dieser Quelle 

nach 

komplexe 

(Senke) 

Bestimmu 

Pot 

+Q !Q 

4. Dipol: F (z) =Cz n v = u r sin + u cos = 

m 

In Polarkoordinaten kann man die Geschwindigkeit des Potentialwirbels Ein Potentialwirbel 

Inwieder Polarkoordinaten leicht angeben, kannwenn man die Geschwindigkeit Zirkulation vorgegeben wieder leicht angeben, wenn die Zirkula 

Q 

Zirkulation 

⇥r e i 

Quelle 

Senke 

funktion bis 

mit 

auf 

Ursprung mit 

eine irrelevante Ursprung z =0 in z = z 0 kann wieder leicht durch eine 2⇥r 

2 

⇥z . = Cr n e in , n > 0 . 

cos n 

x 

Da Betrachten F (z) keine Singularitäten zunächst unmotiviert (2.16c) aufweistdie verschwindet folgende Funktion die komplexe Zirkulation Koordinatentra identisch : 


2x 

Ursprung in z = Integrationskonstante 

funktion findet man bis 

als die auf y komplexe eine irrelevante Geschwindigkeit Integrationskons 

auf kartesische wird : Koordinaten 

wird : 

= Q 

sin Q = Geschwindigkeit 

2⇥z¯z ¯z u r =0, u = . 

u r =0, u = (2.13a). 

⇥ F (z) = Q Potentiallinie 

ln z. 

2⇥r 

2 y 

2 ln z + ⇥ stimmt werden w(z) = M 0: 

Da sie analytisch 

⇥ F (z) = i ln z. 

z ⇥ 

⇥ 2⇥ Q ⇥z 2 . 

C =0 

(2 

F (z) = M ist, stellt sie irgendeine Potentialströmung dar, deren komplexe Geschw 


Stromlinie 

F (z) =Cz n 

Ursprung F (z) = in z i⇥z ln z. 

⇥ w = u iv = 

2⇥ z . = Cr n e in , n > 0 . 

ln(z z 0 ) . 

w 2⇥r 

2 y i 2⇥r 

2⇥r Ein Potentialwirbel mit Ursprung 2⇥ in 2⇥r z = z 2⇥ 2 x 

0 : 

Für 1 sin n Keilströmung Keilströmung ⇥ w(z) = dF 

⇥ ⇥ 0 

Da sie analytisch 0 kann wieder leicht durch eine Koordinatentransformatio 

Q 

cos = Mittels 

2⇥z . Transformation auf kartesische Koordinaten Mittels Transformation auf kartesische Koordinaten Wenn der Ursprung in z = z 0 und nicht in z =0 

2⇥r 

2 x 

Wenn der Ursprung in z = z 0 und nicht in z =0liegt, kann = man i das komplexe Potential durc 

F (z) = Q⇥ stimmt werden 

2⇥r 

2 (x iy) = i ¯z 

w(z) F = M ist, dz = 

⇥(z ⇥z 2 . 

stellt nCzn 1 = nCr n 1 i(n 1) 

e 

(2.16d) 

z 0 ) . 

sie irgendeine Potentialströmung dar, deren komplexe Geschw 

Keilströmung 

Betrachten Betrachten ist. wir Inzunächst Polarkoordinaten wir zunächst unmotiviert unmotiviert die folgende die folgende Funktion Funktion 

2⇥z¯z 

beschreibt dieses komplexe 

dieser Quelle Keilströmung 

u = u 

(Senke) r cos u sin = 

mit Ursprung in z =0folgt nach Bestimmung Potential u = u r cos u sin = 

der Stammlevante 

Integrationskonstante als 

2⇥r 

2 y 

2⇥r 

2 y 

Abbildung bestimmen als x 

e Geschwindigkeit z . Potential die Strömung entlang Abbildung Ursprung 

eines ⇥bestimmen Keiles w(z) in z = mit 

z dF als dem 

F (z) = M iist das ln(zDipolmoment. 

0 : 

Ö nungswinkel 

Betrachten wirz zunächst 0 ) dz = erhält man durch Vergleich mit der Transformationsbeziehung für 

nCzn 1 = nCr n 1 i(n 1) 

e 

. unmotiviert die folgende Funktion 

= i 

(2 

2⇥ 2⇥z 

F (z) =Cz F (z) w n =Cz =(u = 

v = u r sin + u cos = v = u r sin + u cos = 

Geschwindigkeit 2⇥r 

2 x 

2⇥r 

2 x 

F (z) = Q 2⇥ ln(z Stromlinie 

Wäre nun z 0) . 

2⇥r 2 y Q i beschränkt 

2⇥r 2 x dann würden sich Quelle und 5. Keilströmung: 

Senke F (z) F (z) 

annihilieren = = Q Cr n n = M 

und man erhielte keine besonders 

2⇥⇥(z ln(z e in Cr n e r iu )e , 

z z n i 

0 ) 0) . > , 0 n . > 0 . 

ist. In Polarkoordinaten . 

und durch Bildung der Stammfunktion bis auf ei 

y 

F (z) =Cz n erhält 

= Cr n e in man durch Vergleich mit der Transformationsbeziehung für 

, n > 0 . 

interessante Strömung. Wenn aber Q ⌅ 1/⇥ erlaubt Da siewird, Da analytisch woraus sie 

Mdann analytisch 

ist lim Q⇥ beschränkt. Man bezeichnet des Potentialwirbels daher mit Ursprung z =0 

¯z 

F das 

ist, 

(z) ⇤ 

Dipolmoment. 

stellt ist, sie stellt irgendeine sie irgendeine Potentialströmung dar, deren dar, deren komplexe komplexe Geschwindigkeit 

w =(u =Cz n 0 , 

M (x . = iy) lim findet = Q⇥man ials Dipolmoment die komplexe Geschwindigkeit 

da die Potentiallinien den Da findet sie Feldlinien man analytisch r iu )e i 

dieeines komplexe ist, elektrischen (2.13b) stellt (2.14a) Geschwindigkeit 

sie irgendeine Dipols entsprechen. Potentialströmung dar, deren komplexe Geschw 

⇤ 0 2⇥z¯z w 

5. Keilströmung: 

⇥ F (z) = i ln z. 

Man kann dann für das komplexe Potential 

z 0 und nicht = ⇥i in 

w 

z 

= 

=0liegt, 

u iv = 

kann man das komplexe Potential ... in durch 

w Polarkoordinaten 

= u 

eine 

iv 

einfache 

2⇥r 

2 y i 2⇥r 2 x 

2⇥r 

2 y i des Dipols C 

2⇥r 2 x schreiben beliebige 

⇥ w(z) dF 

Konstante, dz n>0. 

2⇥ 

In Polarkoordinaten kann man die Geschwindigkeit wieder leicht angeben, wenn die Zirkula 

2⇥z 

!="/n w ⇥ w(z) = dF = nCzn 1 = nCr n 1 i(n 1) 

⇥ w(z) = u dF 

r = e 

dz = nCr nCzn n 1 cos 1 = nnCr n 1 i(n 1) 

e 

woraus 

= i 2⇥r 

2 (x iy) = i ¯z 

= i 2⇥r 

2 (x iy) = i ¯z wird : 

Stammfunktion F (z) = M F Ein Potentialwirbel mit Ursprung in z = z 0 ka 

w(z) =Cz =nCz n dz n , 

= nCzn 1 = nCr n 1 i(n 1) 

= ⇥ e 

n 

ist. In Polarkoordinaten ist. und In Polarkoordinaten erhält man erhält 1 =(u durch man r Vergleich durch iu )e Vergleich i mit , dermit Transformationsbeziehung der für diefür Geschw die G 

u 

bis auf eine irrelevante Integrationskonstante das r = nCr 

komplexe n 1 cos n 

Potential stimmt (2.15a) werden 

z 

x 

(2.14a) 

2⇥z¯z C 

ist. 

beliebige Polarkoordinaten 2⇥z¯z 

it Ursprung in z =0 

r =0, 

nCr Konstante, n 

u 1 erhält 

= 

cos n n>0. 

man durch Vergleich mit der Transformationsbeziehung für d 

w =(uw =(u r iu )e i 

r 

u iu = )e nCr i n 1 sin n, 

. 

zworaus 0 ) . die komplexe Geschwindigkeit 

und 

= i (2.13c) 2⇥r F (z) = i ln(z z 

= 0 ) . 

2⇥ 2⇥z w(z) u w =(u = =nCz nCr n 1 sin =(u n r . iu )e i r iu )e i 

2⇥z 

, 

ln z. 

Mittels Transformation(2.14b) 

auf kartesische Koordinaten 

w(z) und durch = dF Bildung der Stammfunktion bis auf eine undirrelevante durch Bildung Integrationskonstante der Stammfunktion dasbis komplexe auf einePotential 

irrelevante Integrationskonstante das k 

t Ursprung des Potentialwirbels in z dz = = M woraus woraus folgt. O ensichtlich beschreibt dieses komplexe Potential die Strömung entlang eines Keile 

⇥ u = n nCr cos n , 

z 0 kann z 2 woraus r nCr n 1 n cos 1 sin n 

= ⇥/n 

n , 

mit wieder Ursprung leicht in durch z =0 eine Koordinatentransformation des Potentialwirbels u = u r cos mit u sin Ursprung be-= 2⇥r in z 2 y 

(2.15b) 

u u r = nCr =0 

u ⇤ = Cr n 

nCr 1 r = nCr n 1 cos n cos 

sin n n 1 n 

folgt. O ensichtlich sin . n . 

entialfunktion lautet 

n 1 

beschreibt dieses komplexe Potential y die Strömung entlang eines Keile

Superpositionsprinzip 


!=const 

ann. Dazu überlagern wir eine Parallelströmung mit je einem Dipol und einem Potentialwirbel 


Das zugehörige komplexe Potential ist 

mungenFluidmachanik II 

38 Daraus folgt das komplexe Potential durch Bildung der Stammfunktion ( 

⇥ y 

z 

y’ 37 

z’ 

Das komplexe Potential ist 

Ums , 

z 

Dr. 

+ Prof. R2 S. Viele Dr. Hickel 

i N. ln Potentialströmungen z, A. Adams , Dr. S. können Hickel durch Superposition konstante von Elementarströmungen hier zuDas Nullkomplexe gesetztbeschrieben wurde) Potential istwerden. Beispiel: 

z 2⇤ ⇥ 

Das komplexe Potential ist 

Zylinderumströmung = Parallelströmung + Dipol Potential F (z) =U( ⇥ Dipolmoment: z + R2 

⇥ 

e komplexe Geschwindigkeit y a 

! 

beeinflussen iR kann. Dazu überlagern , wir M = eine ⇥RParallelströmung 2 U ⇥ ,) 

mit je einem 

F (z) =(U iV )z F (z) . ⇥z 

=U ⇥ z + R2 

, M = ⇥R 2 U ⇥ , 

R 2 ⇥ 

# 

im Ursprung. Das zugehörige 

F (z) =U ⇥ z + R2 komplexe Potential z S 

, M = ⇥R 2 ist 

U 1 

U ⇥ , 

z 2 i 1 

S 2 

x 

2⇤z 

S’ 

Lösung wobei man noch a’ 

S der Übungsklausur Lösung der Übungsklausur Da F (z) keine Singularitäten 

bestätigen z ⇥ muß, daß diese Wahl von M tatsächlich al 

wobei man aufweist verschwindet die komplexe Zirkulat 

Ursprung Zirkulation F (z) =U mit demz + Radius R2 noch bestätigen muß, daß diese Wahl von M 

R ergibt. i ln z, 

te mit u = v =0liegen in ! 

−R wobei man noch bestätigen z muß, 2⇤ daß diese Wahl von M tatsächlich als S 

38 

Ursprung R 

Die komplexe C =0 Geschwindigkeit x’ 

mit 38 dem Radius R ergibt. 

berechnet man als 

R := Radius des Zylinders Ursprung mit dem Radius R ergibt. 

e i woraus sich die komplexe Die komplexe Geschwindigkeit Geschwindigkeit berechnet man als 

s =i ± ⌅ 1 2 

S 38 

32, = 1 

S 2 

x 

4⇤U R 

38 Geschwindigkeit 

R 2 Potentialströmungen 

⇥ 

Die komplexe Geschwindigkeit 

w(z) =U ⇥ 1 

r 2 e berechnet 2i man als 

R 2 ⇥ 

, R 

w(z) =U 1 

R 2 

z 

w(z) =U ⇥ 1 

2 i 2 ⇥ 

die LageFragenteil: 

der Staupunkte durch die Wahl von wie gewünscht beeinflussen. 

beeinflussen −iR kann. Dazuw(z) überlagern beeinflussen 

=U 2⇤z ⇥ 

wir 1 eine kann. Parallelströmung 

und den Geschwindigkeitsbetrag, r 2 e 2i r 

, 

2 e Dazu 2i , 

überlagern mitwir je einem 

P 

ir zunächst den für Anwendungen wichtigen Fall, in dem die Staupunkte auf dem Zylinder beeinflussen 2Das Potentialströmungen 

komplexe 

kann. 

Potential 

Dazu überlagern 

ist 

im 

st also r s = R und sin ⇥ s = mit | | ⇥ 1. 

⇥ 

Ursprung. 

wir eine 

Das 

Parallelströmung 

zugehörige komplexe 

mit je 

Poten 

einem 

im Ursprung. Das zugehörige komplexe Potential ist 

Das Vorzeichen der Zirkulation bestimmt den Umlaufsinn beeinflussen : > 0 resp. dessen Quadrat als 

ergibt. im Ursprung. kann. bedeutet 

Das zugehörige DazuUmlauf überlagern im math. pos. Sinn, 

Zylinderumströmung mit Staupunktverschiebung Potential F (z) =Uund ( Dipolmoment 

den Geschwindigkeitsbetrag, Zirkulation 

resp. dessen Quadrat 

) 

a 

y 

⇥ z + R2 ⇥ komplexe wir eine Potential Parallelströmung 

, M = ⇥R 

= Parallelströmung + Dipol + Potentialwirbel 

q 2 = U⇥ 2 2R 2 

⇥ 

2 ist ⇥ mit je einem 

< 0 bedeutet Umlauf im math. neg. Sinn. Gemäß U ⇥ , 

imDefinition und 

Ursprung. der komplexen 

Die Staupunkte den Geschwindigkeitsbetrag, mit u = v =0liegen 

z 

Zirkulation ⇥ muß für den 

F (z) =U Das zugehörige z + R2 komplexe 

resp. F (z) R4 dessen 

Potential 

in =U Quadrat z ist + R2 

Potential ist1. 

i ln z, 

als 

1 

r 2 cos 2 + 

r 4 . 

DieZirkulation 

q 2 U 2 2R 2 

⇥ 

z s 

R4 

R 

1 

Staupunkte = r q 2 s 

R ei s =i ± ⌅ = U 2 2R 2 

⇥ i ln z, 

Potentialwirbel Q ist die 

F (z) 

Quellenstärke,für 

=U z + R2 Q>0 

i 

spricht 

ln z, 

man von einer z Quelle 

R4 2⇤ für Q

Grenzschichtströmungen 

Grenzschichtgleichungen 

Kontinuitäts- und Impulsgleichung vereinfachen sich in ebenen, 

inkompressiblen Grenzschichten zu den Grenzschichtgleichungen 

mit folgenden Randbedingungen: 

Haftbedingung and der Wand 

Außenrand 

Einströmrand 

Der Druck kann auch vollständig aus den Grenzschichtgleichungen eliminiert werden, vgl. Bernoulli: 

Definitionen 

99%-Grenzschichtdicke 

Verdrängungsdicke 

Impulsverlustdicke 

Lauflängen-Reynolds-Zahl, x wird von der Plattenvorderkannte gemessen 

Wandschubspannung 

Reibungsbeiwert 

Widerstandsbeiwert pro Einheitsbreite 

von-‐Kármán-‐Impulsintegral 

Für Grenzschichten an ebenen Platten bei Parallelströmung im Außenbereich gilt die integrale Impulsgleichung 

Blasius Grenzschicht 

Grenzschichtdicken 

Reibungs- und Widerstandsbeiwert 

und somit 

O l2 2 

1 

Re 

⇥ 

= O[1] 

Die für eine Grenzschicht vereinfachten Impulsgleichungen stellen zusammen mit der Kontinuitätsgleichung 

die Grenzschichtgleichungen dar: 

⌅u 

⌅x + ⌅v 

⌅y =0, 

(3.4a) 

u ⌅u 

⌅x + v ⌅u 

⌅y = 

1 ⇤ 

dp 

dx + ⇥ ⌅2 u 

⌅y 2 , (3.4b) 

Die Lösung dieser Gleichungen kann mit den folgenden Randbedingungen (im allgemeinen numerisch) berechnet 

werden. An der Wand gilt die Haftbedingung 

u(x, y = 0) = 0 , 

(3.4c) 

v(x, y = 0) = 0 . 

(3.4d) 

Am Einströmrand gilt die Einströmrandbedingung 

u(x = x 0 ,y)=u 0 (y) . 

(3.4e) 

Am äußeren Rand bei großen y gilt die Außenrandbedingung 

u(x, y ⇤⌅)=U ⇥ , 

(3.4f) 

die in der numerische Behanldung meist bei einem festen y, daß ausreichend groß gewählt wird, aufgeprägt 

wird. Man beachte daß die Grenzschichtgleichung vom parabolischen Typ in x sind. Eine zusätzliche 

Randbedingung in x, stromab vom Einströmrand, darf daher nicht aufgeprägt werden. 

Im Sinne der gekoppelten Potentialströmungs-Grenzschicht-Verfahren wäre es sinnvoll, die Außenrandbedingung 

durch die vom potentialtheoreitschen Verfahren gelieferte Wandgeschwindigkeit u ⇥=0 (x, y = 0) 

auszudrücken. Hierzu macht man die wandnormale Koordinate zunächst auf einmal in der reibungsfreien 

Betrachtung und dann in der reibungsbehafteten Betrachtung dimensionslos. Man erhält also ỹ = y/l 

bzw. y = y/ als dimensionslose Wandabstände. Mit (3.3) kann man y = y ⇧ Re/l = ⇧ Reỹ schreiben, 

repsektive ỹ = y / ⇧ Re. Wählt man nun in der reibungsbehafteten Beschreibung einen dimensionslosen 

Wandabstand y fest und betrachtet wie sich der zugehörige Wandabstand ỹ bei wachsendem Re verhält , 

O 2 Re = O[1] 



⌅u 

⌅x + ⌅v 

⌅y =0, 

(3.4a) 

u ⌅u 

⌅x + v ⌅u 

⌅y = 

1 ⇤ 

dp 

dx + ⇥ ⌅2 u 

⌅y 2 , (3.4b) 



u(x, y = 0) = 0 , 

(3.4c) 

v(x, y = 0) = 0 . 

(3.4d) 


u(x = x 0 ,y)=u 0 (y) . 

(3.4e) 


u(x, y ⇤⌅)=U ⇥ , 

(3.4f) 











l 

Betrachten wir die stationäre Impulgleichung in y-Richtung 

u ⌅v 

⌅x + v ⌅v 

⌅y = 

1 ⇤ 

⌅p 

⌅y + ⇥ ⌅2 v 

⌅x 2 + ⇥ ⌅2 v 

⌅y 2 , 

dann stellen wir durch Analyse der Größenabschätzungen für die einzelnen Terme 

fest, daß alle Terme bis auf den Druckgradienten verschwinden. Some wird die reduz 

y-Richtung für Grenzschichten reduziert zu 

⌅p 

⌅y =0. 

Als Folge ist der Druck p konstant in y über die Grenzschicht hinweg und nur von x ab 

ist gegeben durch den Druck in der Außenströmung und die resultierenden Druckkräfte 

(schlanken) Körper mit ausgebildeter und anliegender Grenzschicht (siehe hierzu au 

alleine das Ergebnis der reibungsfreien Außenströmung. Diese Tatsache macht man s 

zunutze: der Auftrieb als Druckresultierende (bzw. auch der induzierte Widerstand 

Strömung bei hohen Reynoldszahlen näherungsweise unabhängig von der Reynoldsz 

den Widerstand (insbesondere den Reibungswiderstand). 

Die Größenabschätzung für die Terme der stationären x-Impulsgleichung liefert: 

u ⇤u 

⇤x 

+v ⇤u 

⇤y = 1 ⇥ 

dp 

dx 

+⇥ ⇤2 u 

⇤x 2 

+⇥ ⇤2 u 

⇤y 2 

⌅ ⌅ ⌅ ⌅ ⌅ 

O 

⇧ 

U 2 

l 

⌃ 

O l U U ⇥ O 

⇧ 

1 

⇥ 

⇥U 2 

l 

⌃ 

O ⇥ U l 2 ⇥ 

O ⇥ U 2 

⇥ 

⌅ ⌅ ⌅ ⌅ ⌅ 

O[1] O[1] O[1] O 1 Re 

⇥ 

O 

⇧ 

l 2 2 

1 

Re 

⌃ 

Was passiert mit nun l2 2 

1 

Re für Re ⇤⌃? Hierzu macht man eine Fallunterscheidun 

1. : 

2 

l 2 

⇤ 0 langsamer als 1 Re ⇧. Dann ist 

O 

⇤ l 2 

2 

1 

Re 

⌅ 

= O 

⇤ 1 Re⌅ 

. 

Dieser Fall würde bedeuten, daß für große Re der Grenzfall der reibungsfreien 

schicht vorliegt. Dann kann die Haftbedingung an der Wand aber nicht erfüllt 

der Fall physikalisch unsinnig. 



⌅u 

⌅x + ⌅v 

⌅y =0, 

(3.4a) 

u ⌅u 

⌅x + v ⌅u 

⌅y = 

1 ⇤ 

dp 

dx + ⇥ ⌅2 u 

⌅y 2 , (3.4b) 



u(x, y = 0) = 0 , 

(3.4c) 

v(x, y = 0) = 0 . 

(3.4d) 


u(x = x 0 ,y)=u 0 (y) . 

(3.4e) 


u(x, y ⇤⌅)=U ⇥ , 

(3.4f) 












⌅u 

⌅x + ⌅v 

⌅y =0, 

(3.4a) 

u ⌅u 

⌅x + v ⌅u 

⌅y = 

1 ⇤ 

dp 

dx + ⇥ ⌅2 u 

⌅y 2 , (3.4b) 



u(x, y = 0) = 0 , 

(3.4c) 

v(x, y = 0) = 0 . 

(3.4d) 


u(x = x 0 ,y)=u 0 (y) . 

(3.4e) 


u(x, y ⇤⌅)=U ⇥ , 

(3.4f) 











⌅x ⌅y ⇤ dx ⌅y 



u(x, y = 0) = 0 , 

(3.4c) 

v(x, y = 0) = 0 . 

(3.4d) 


u(x = x 0 ,y)=u 0 (y) . 

(3.4e) 


u(x, y ⇤⌅)=U ⇥ , 

(3.4f) 












⌅u 

⌅x + ⌅v 

⌅y =0, 

(3.4a) 

u ⌅u 

⌅x + v ⌅u 

⌅y = 

1 ⇤ 

dp 

dx + ⇥ ⌅2 u 

⌅y 2 , (3.4b) 



u(x, y = 0) = 0 , 

(3.4c) 

v(x, y = 0) = 0 . 

(3.4d) 


u(x = x 0 ,y)=u 0 (y) . 

(3.4e) 


u(x, y ⇤⌅)=U ⇥ , 

(3.4f) 











3 Grenzschichten 57 

stellt man fest, daß ỹ ⇤ 0. D.h. insbesondere y 

=1, d.h. der Grenzschichtrand, stimmt in der reibungsfreien 

Betrachtung im Grenzfall großer Reynoldszahlen mit der Position der Wand in ỹ =0überein. Daher 

können wir alternativ zu (3.4f) auch vorschreiben, daß 

u(x, y = )=u ⇥=0 (x, y = 0) . (3.4g) 

Weiterhin kann man der Druck vollends eliminieren, indem man ausnutzt, daß in der Außenströmung die 

Bernoulli-Gleichung gilt, und man erhält folgenden Zusammenhang zwischen p(x) und U (x) : 

1 

⌅ 

dp 

dx = U dU 

dx . (3.5) 

Alternativ zu (3.4b) erhält man dann: 

u ⇧u 

⇧x + v ⇧u 

⇧y = U dU 

dx + ⇤ ⇧2 u 

⇧y 2 . (3.6) 

3.1.1 Blasius Grenzschicht 

Ein wichtiger Spezialfall ist die Grenzschicht an einer ebene Platte mit dp/dx =0. In diesem Fall gelten 

folgende Randbedingungen: 

u(x ⇥ 0,y ⇤⌅)=U (x) =U ⇥ , 

(3.7a) 

u(x >0,y = 0) = 0 , 

(3.7b) 

v(x >0,y = 0) = 0 . 

(3.7c) 

Die Einströmrandbedingung ist: 

u(x =0,y >0) = U ⇥ . 

(3.7d) 

Die Grenzschichtgleichungen vereinfachen sich zu 

⇧u 

⇧x + ⇧v 

⇧y =0, 

(3.7e) 

u ⇧u 

⇧x + v ⇧u 

⇧y = ⇤ ⇧2 u 

⇧y 2 . (3.7f) 

Die Lösung dieser Gleichungen wurde in allgemeiner Form von Blasius 1908 ermittelt. Hierzu machte Blasius 

einen 

Ähnlichkeitsansatz , der erlaubte die beiden unabhängigen Variablen x und y auf eine unabhängige 

Variable ⇥ zurückzuführen. Die physikalische Begründung für den Ähnlichkeitsansatz ist wie folgt. Zunächst 

macht man x und y mit den jeweiligen Längenskalen dimensionslos: 

x = x/l , y = y = y 

⇥ 

⇥l 

U 

. 

Da wegen des parabolischen Charakters der Grundgleichungen die Grenzschicht an einer Stelle x unbeeinfluß 

von der Längenskale l sein sollte, muß diese Längenskale eliminierbar sein. Eine Kombination von x 

und y 

so, daß die Längenskale l herausfällt, liefert die Ähnlichkeitsvariable 

⇥ = 

y 

⇧ x = 

y 

⇤x/U ⇥ . (3.8) 

v = 

v 

⇤U ⇤ /x = 1 2 (⇥f ⇥ f) . (3.10b) 

Eingesetzt in die Grenzschichtgleichgungen liefern diese Ausdrücke folgende gewöhnliche Di erentialgleichung 

für f(⇥): 

f ⇥⇥⇥ + 1 2 ff⇥⇥ =0. 

(3.11a) 

Diese Di erentialgleichung wird ergänzt durch folgende Randbedingungen: 

u(x, y = 0) = 0 ⌅ f ⇥ (⇥ = 0) = 0 , 

(3.11b) 

v(x, y = 0) = 0 ⌅ f(⇥ = 0) = 0 , 

(3.11c) 

u(x, y ⇥⇧)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1, 

(3.11d) 

u(x =0,y)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1. 

(3.11e) 

Diese Di erentialgleichung stellt ein nichtlineares gewöhnliches Randwertproblem dar, das nicht mehr geschlossen 

gelöst werden kann. Die Lösung wird numerisch, meist durch ein sogenanntes Schießverfahren, 

bestimmt und liefert als Ergebnis die sogenannte Blasius-Grenzschicht . 

Anstelle der Grenzschichtdicke verwendet man in der Praxis oft die sogenannte 99%-Grenzschichtdicke , 

deren allgemeine Definition lautet 

99 = y(u =0.99U ⇤ ) . (3.12) 

Für die Blasius Grenzschicht ist die Verwendung dieser Definition der Grenzschichtdicke angebracht, da 

u(y = 

)=U ⇤ nur asymptotisch für y ⇥⇧erreicht wird. 

Für Blasius Grenzschicht ermittelt man aus der Lösung der obigen Di erentialgleichung folgende Abhängigkeit 

von der sogenannten Lauflängen-Reynoldszahl Re x = Ux/⇤, wobei x die von der Plattenvorderkante gemessene 

” Lauflänge“der Grenzschicht ist: 

99 

x = 4.9 

⌃ Rex , (3.13) 

mit 

Re x = U ⇤x 

⇤ 

. 

Typische Werte für (3.13)sind z.B. für Wasser mit U ⇤ =1m/s, bei einer Lauflänge von 1m, Re x ⇤ 67000 

und 99 ⇤ 0.019 m. 

0 

Für die Blasius Grenzschicht ist 

C w = 1.328 

⇧ Rex . (3.18) 

Man kann auch die Vertikalgeschwindigkeit in Abhängigkeit von x angeben als 

v 

U ⇥ = 1 2 

1 

⇧ Rex (⇥f f) , (3.19) 

Man stellt fest, daß v für y ⇥⌅einen endlichen Wert annimmt 

v 

U ⇥ ⇤ 0.861 

1 

⇧ Rex , (3.20) 

was in der physikalischen Realität nur bedingt sinnvoll ist, da man erwartet, daß in großer Entfernung von 

der Grenzschicht der Verdrängungse ekt der Grenzschicht verschwindet. Dieser Widerspruch illustriert die 

Gültigkeitsgrenzen der Grenzschichtbeschreibung. 

Ein besser definiertes Längenmaß für die Grenzschicht als die Grenzschichtdicke ist die Verdrängungsdicke , 

deren allgemeine Definition lautet : 

1 = 

⌅ ⇥ 

0 

⇥ 

1 

u 

U 

⇤ 

dy . (3.21) 

Beachte hierbei, daß für den Fall, daß u(y) in y = u(y = )=U annimmt, u(y) =U für y> 

fortgesetzt wird. In diesem Fall kann man die Verdrängungsdicke auch wie folgt definieren 

1 = 

⌅ 

0 

⇥ 

1 

u 

U 

⇤ 

dy 

Gemäß der folgenden Skizze gibt die Verdrängungsdicke also an, um wieviel die Körperkontur aufgedickt 

werden muß um bei einer reibungsfreien Beschreibung den gleichen Massenstrom zu erzielen: 

! 1 

Man erkennt anhand der Definition, daß die Verdrängungsdicke auch für den Fall, daß die Außenströmungsgeschwindigkeit 

nur im Grenzfall y ⇤⇧erreicht wird, beschränkt bleibt. Für die Blasius Grenzschicht ist mit U = U 

1 =1.72 

⇧ ⇥x 

U . (3.22a) 

Die im nächsten Abschnitt definierte Imulsverlustdicke berechnet man für die Blasius Grenzschicht als 

2 =0.664 

⇧ ⇥x 

U . (3.22b) 

3.1.2 Von Kármán Impulsintegral 

Die sogenannte Impulsverlustdicke ergibt sich, wenn man die oben angestellte Überlegung für die Verdrängungsdicke 

auf den Impuls überträgt: 

2 = 

⌅ 

0 

u 

U 

⇥ 

1 

u 

U 

⇤ 

dy . (3.23) 

Beachte, daß hier ebenfalls wie bei der Verdrängungsdicke u(y) =U für y> gilt, falls u(y = )=U . 

Also kann man obige Gleichung in diesem Fall ersetzten durch 

2 = 

⌅ 

0 

u 

U 

⇥ 

1 

u 

U 

⇤ 

dy 

Da die Wirkung der Grenzschicht bei großen Wandabständen nicht mehr spürbar sein soll müssen die Ableitungen 

⇥u 

⇥y , ⇥2 u 

⇥y 2 , ... für y ⇤⇧verschwinden. Durch Integration der Grenzschichtgleichungen über y erhält 

man dann 

⌅ 

0 

⇥ 

u ⇧u 

⇧x + v ⇧u 

⇧y 

⇤ 

dy = 

⌅ 

0 

u du 

dx dy + ⌅ 

0 

µ 

⇤ 

⇧ 2 u 

⇧y 2 dy 

⌅ 

⌅ 

0 

⇥ 

u ⇧u 

⇧x 

u du 

dx + v ⇧u 

⇧y 

⇤ 

dy = µ ⇤ 

⇧u 

⇧y 0 = ⌅ w 

⇤ 

(⇥) . 

Aus der Kontinuitätsgleichung folgt 

v = 

⌅ y 

0 

⇧v 

⇧y dy = 

y 

⌅ 

0 

⇧u 

⇧x dy , 


für f(⇥): 

f ⇥⇥⇥ + 1 2 ff⇥⇥ =0. 

(3.11a) 


u(x, y = 0) = 0 ⌅ f ⇥ (⇥ = 0) = 0 , 

(3.11b) 

v(x, y = 0) = 0 ⌅ f(⇥ = 0) = 0 , 

(3.11c) 

u(x, y ⇥⇧)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1, 

(3.11d) 

u(x =0,y)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1. 

(3.11e) 






99 = y(u =0.99U ⇤ ) . (3.12) 


u(y = 





99 

x = 4.9 

⌃ Rex , (3.13) 

mit 

Re x = U ⇤x 

⇤ 

. 

Typische Werte für (??)sind z.B. für Wasser mit U ⇤ =1m/s, bei einer Lauflänge von 1m, Re x ⇤ 67000 

und 99 ⇤ 0.019 m. 


Die allgemeine Definition des sogenannten Reibungsbeiwertes ist 

C f = 

⇧ W 

⇥ 

2 U 2 ⇥ 

, (3.14) 

wobei die Wandschubspannung 

⇧ W = ⌅⇤ ⌃u 

⌃y y=0 (3.15) 

verwendet wird. 

Für die Blasius Grenzschicht verhält sich C f (x) gemäß 

C f = 0.664 

⇧ Rex . (3.16) 

Die allgemeine Defintion des Widerstandsbeiwertes pro Einheitsbreite ist 

C w = 1 l 

⌅ l 

0 

C f dx . (3.17) 


C w = 1.328 

⇧ Rex . (3.18) 


v 

U ⇥ = 1 2 

1 

⇧ Rex (⇥f f) , (3.19) 


v 

U ⇥ ⇤ 0.861 

1 

⇧ Rex , (3.20) 





C f = 

⇧ W 

⇥ 

2 U 2 ⇥ 

, (3.14) 


⇧ W = ⌅⇤ ⌃u 

⌃y y=0 (3.15) 



C f = 0.664 

⇧ Rex . (3.16) 


C w = 1 l 

⌅ l 

0 

C f dx . (3.17) 


C w = 1.328 

⇧ Rex . (3.18) 


v 1 1 



C f = 

⇧ W 

⇥ 

2 U 2 ⇥ 

, (3.14) 


⇧ W = ⌅⇤ ⌃u 

⌃y y=0 (3.15) 



C f = 0.664 

⇧ Rex . (3.16) 


C w = 1 l 

⌅ l 

0 

C f dx . (3.17) 


C w = 1.328 

⇧ Rex . (3.18) 


v 

U ⇥ = 1 2 

1 

⇧ Rex (⇥f f) , (3.19) 


v 

U ⇥ ⇤ 0.861 

1 

⇧ Rex , (3.20) 



Gültigkeitsgrenzen der Grenzschichtbeschreibung. 

Ein besser definiertes Längenmaß für die Grenzschicht als die Grenzschichtdicke ist die Verdrängungsdicke , 

deren allgemeine Definition lautet : 


da v(y = 0) = 0. 

⇤ 

⇥ 

0 

v ⌅u 

⌅y dy = 

⇥ 

0 

⌅ 

⌃ 

y 

0 

⌅u 

⌅x dy ⇧ 

⌥ ⌅u 

⌅y dy 

= 

y 

0 

⌅u 

⌅x dyu ⇥ 

0 

+ 

⇥ 

0 

⌅u 

⌅x udy 

= 

⇥ 

0 

⌅u 

⌅x dyu + ⇥ 

0 

u ⌅u 

⌅x dy . 

Dies eingesetzt in (⇥) gibt 

⇥ 

0 

⇥ 

u ⌅u 

⌅x 

u du 

dx 

u ⌅u 

⌅x + u⌅u 

⌅x 

⇤ 

dy = 

⇤ w 

⇥ 

⇤ 

⇥ 

0 

u ⌅(u u) 

⌅x 

dy + 

⇥ 

0 

(u u) ⌅u 

⌅x dy + ⇥ 

0 

(u u) du 

dx dy = ⇤ w 

⇥ 

⇤ d 

dx 

⇥ 

0 

u (u 

u) dy + du 

dx 

⇥ 

0 

(u u) dy = ⇤ w 

⇥ 

⇤ d 

dx 

⌅ 

⌃u 2 

⇥ 

0 

u 

u 

⇥ 

1 

u 

u 

⇤ 

dy 

⇧ 

⌥ + du 

dx u 

⇥ 

0 

⇥ 

1 

u 

u 

⇤ 

dy = 1 2 

⇤ w ⇥ 

2 

. 

Für eine Parallelströmung u (x) im Außenbereich erhält man dann nach Division beider Seiten mit u 2 

d 2 

dx + 1 u 

du 

dx ( 1 +2 2 )= 1 2 C f . (3.24) 

Dies ist die integrale Impulsgleichung für Grenzschichten an ebenen Platten nach von Kármán und Pohlhausen 

(1921). 

3.1.3 Pohlhausen Grenzschicht 

Die Grenzschichtlösung nach Pohlhausen beruht auf einer näherungsweisen Lösung der integralen Impulsgleichung. 

Mit einem Polynomansatz für u(y) gemäß 

u = a + by + cy 2 + dy 3 , 

wobei y 

= y/ (x), läßt sich eine Lösung von (3.24) konstruieren: 

u = 3 2 y 1 

2 y 3 . 

58 3 Grenzschichten 

Entsprechend entdimensionalisiert man die x-Geschwindigkeit und die Stromfunktion: 

u = 

u 

U ⇤ , 

f(⇥) = 

⌅ 

⌃ ⇤xU⇤ . (3.9) 

Drückt man die dimensionslosen Geschwindigkeiten durch die Stromfunkion aus, so erhält man 

u = f ⇥ (⇥) , 

(3.10a) 

v = 

v 

⇤U ⇤ /x = 1 2 (⇥f ⇥ f) . (3.10b) 


für f(⇥): 

f ⇥⇥⇥ + 1 2 ff⇥⇥ =0. 

(3.11a) 


u(x, y = 0) = 0 ⌅ f ⇥ (⇥ = 0) = 0 , 

(3.11b) 

v(x, y = 0) = 0 ⌅ f(⇥ = 0) = 0 , 

(3.11c) 

u(x, y ⇥⇧)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1, 

(3.11d) 

u(x =0,y)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1. 

(3.11e) 






99 = y(u =0.99U ⇤ ) . (3.12) 


u(y = 





99 

x = 4.9 

⌃ Rex , (3.13) 

mit 

Re x = U ⇤x 

⇤ 

. 


und 99 ⇤ 0.019 m. 


! 1 

Man erkennt anhand der Definition, daß die Verdrängungsdicke auch für den Fall, daß die Außenströmungsgeschwindigkeit 

nur im Grenzfall y ⇤⇧erreicht wird, beschränkt bleibt. Für die Blasius Grenzschicht ist mit U = U 

1 =1.72 

⇧ ⇥x 

U . (3.22a) 

Die im nächsten Abschnitt definierte Imulsverlustdicke berechnet man für die Blasius Grenzschicht als 

2 =0.664 

⇧ ⇥x 

U . (3.22b) 


Die sogenannte Impulsverlustdicke ergibt sich, wenn man die oben angestellte Überlegung für die Ver- 



u = 

u 

U ⇤ , 

f(⇥) = 

⌅ 

⌃ ⇤xU⇤ . (3.9) 


u = f ⇥ (⇥) , 

(3.10a) 

v = 

v 

⇤U ⇤ /x = 1 2 (⇥f ⇥ f) . (3.10b) 


für f(⇥): 

f ⇥⇥⇥ + 1 2 ff⇥⇥ =0. 

(3.11a) 


u(x, y = 0) = 0 ⌅ f ⇥ (⇥ = 0) = 0 , 

(3.11b) 

v(x, y = 0) = 0 ⌅ f(⇥ = 0) = 0 , 

(3.11c) 

u(x, y ⇥⇧)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1, 

(3.11d) 

u(x =0,y)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1. 

(3.11e) 






99 = y(u =0.99U ⇤ ) . (3.12) 


u(y = 





99 

x = 4.9 

⌃ Rex , (3.13) 

mit 

Re x = U ⇤x 

⇤ 

. 


und 99 ⇤ 0.019 m. 

60 3 Grenzsc 

! 1 

Man erkennt anhand der Definition, daß die Verdrängungsdicke auch für den Fall, daß die Außenström 

nur im Grenzfall y ⇤⇧erreicht wird, beschränkt bleibt. Für die Blasius Grenzschicht ist mit U = 

1 =1.72 

⇧ ⇥x 

U . 

Die im nächsten Abschnitt definierte Imulsverlustdicke berechnet man für die Blasius Grenzschicht 

2 =0.664 

⇧ ⇥x 

U . 


Die sogenannte Impulsverlustdicke ergibt sich, wenn man die oben angestellte Überlegung für 

drängungsdicke auf den Impuls überträgt: 

2 = 

⌅ 

0 

u 

U 

⇥ 

1 

u 

U 

⇤ 

dy . 



C f = 

⇧ W 

⇥ 

2 U 2 ⇥ 

, (3.14) 


⇧ W = ⌅⇤ ⌃u 

⌃y y=0 (3.15) 



C f = 0.664 

⇧ Rex . (3.16) 


C w = 1 

l 

⌅ 

C f dx . (3.17) 



u = 

u 

U ⇤ , 

f(⇥) = 

⌅ 

⌃ ⇤xU⇤ . (3.9) 


u = f ⇥ (⇥) , 

(3.10a) 

v = 

v 

⇤U ⇤ /x = 1 2 (⇥f ⇥ f) . (3.10b) 


für f(⇥): 

f ⇥⇥⇥ + 1 2 ff⇥⇥ =0. 

(3.11a) 


u(x, y = 0) = 0 ⌅ f ⇥ (⇥ = 0) = 0 , 

(3.11b) 

v(x, y = 0) = 0 ⌅ f(⇥ = 0) = 0 , 

(3.11c) 

u(x, y ⇥⇧)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1, 

(3.11d) 

u(x =0,y)=U ⇤ ⌅ f ⇥ (⇥ ⇥⇧)=1. 

(3.11e) 






99 = y(u =0.99U ⇤ ) . (3.12) 


u(y = 





99 

x = 4.9 

⌃ Rex , (3.13) 

mit 

Re x = U ⇤x 

⇤ 

. 



C f = 

⇧ W 

⇥ 

2 U 2 ⇥ 

, (3.14) 


⇧ W = ⌅⇤ ⌃u 

⌃y y=0 (3.15) 



C f = 0.664 

⇧ Rex . (3.16) 


C w = 1 l 

⌅ l 

0 

C f dx . (3.17) 


C w = 1.328 

⇧ Rex . (3.18) 


v 

U ⇥ = 1 2 

1 

⇧ Rex (⇥f f) , (3.19) 

Für die Grenzschicht kann man aus den Navier-Stokes-Gleichungen vereinfachte Gleichungen unter Aus 

zung der besonderen geometrischen Eigenschaften der Grenzschicht herleiten. Dies sind die sogenan 

Grenzschichtgleichungen . 

Um die geometrischen Besonderheiten einer Grenzschicht zu erkennen, betrachten wir folgende Skizze: 

°° 

! 

!(x) 

u( )=U 

y 

x 

! 

U = U ! 

Die Grenzschicht zeichnet sich durch folgende Geschwindigkeitsskalen und Längenskalen aus: 

Geschwindigkeitsskale in x-Richtung U = U 

: Geschwindigkeit am Grenzschichtrand in x-Richtu 

Längenskale in x-Richtung l (z.B. Sehnenlänge eines Profiles), 

⇥ : Dichte des Fluides (hier ⇥ = const angenommen), 

Längenskale in y-Richtung (x) : Grenzschichtdicke mit u( )=U . 

Mit diesen Skalen kann man in den Navier-Stokes-Gleichgungen auftretende Geschwindigkeitsgradie 

folgendermaßen abschätzen. Betrachten wir zunächst den reibungsfreien Fall, in dem sich keine Grenzsch 

ausbildet. Dann ist die Längenskale in y-Richtung nicht 

wie im reibungsbehafteten Fall, sondern die gle 

Längenskale wie in x-Richtung, nämlich l. Also kann man ⇤u/⇤y abschätzen durch 

⇤u 

⇤y ⇥ U l 

. 

In der reibungsbehafteten Strömung kann aber ⇤u/⇤y abgeschätz werden durch eine finite Di erenz zwisc 

den Werten am Grenzschichtrand und an der Wand 

⇤u 

⇤y ⇥ U 0 

0 = U . 

Da 

⇤ l wird ⇤u/⇤y in einer reibungsfreien Betrachtung viel zu klein abgeschätzt, d.h. die reibungs 

Theorie versagt und kann Grenzschichtphänomene nicht beschreiben. 

//////////////////////////////////////////////////////////////////////

Formelsammlung zur Prüfung Fluidmechanik II

Create successful ePaper yourself

Delete template?

Save as template?