Master Thesis

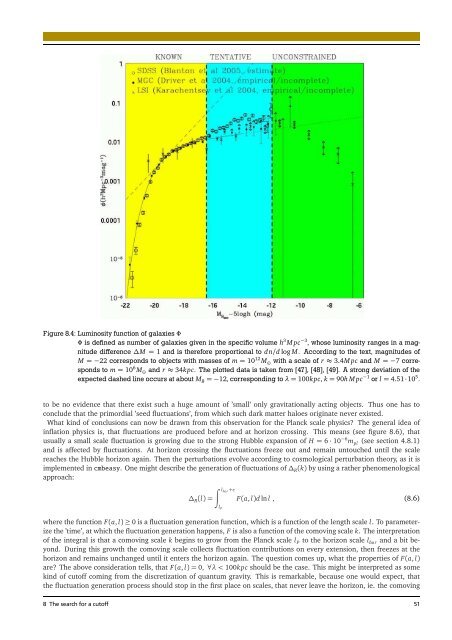
Figure8.4: Luminosityfunction ofgalaxiesΦ
Φ is defined as number of galaxies given in the specific volume h 3 M pc −3 , whose luminosity ranges in a magnitude
difference∆M= 1 and is therefore proportional to dn/d log M. According to the text, magnitudes of
M=−22 corresponds to objects with masses of m=10 12 M ⊙ with a scale of r≈ 3.4M pc and M=−7 corresponds
to m=10 6 M ⊙ and r≈ 34kpc. The plotted data is taken from [47], [48], [49]. A strong deviation of the
expecteddashedlineoccursatabout M B=−12,correspondingtoλ=100kpc, k=90h M pc −1 or l= 4.51·10 5 .
to be no evidence that there exist such a huge amount of ’small’ only gravitationally acting objects. Thus one has to
conclude that the primordial ’seed fluctuations’, from which such dark matter haloes originate never existed.
What kind of conclusions can now be drawn from this observation for the Planck scale physics? The general idea of
inflation physics is, that fluctuations are produced before and at horizon crossing. This means (see figure 8.6), that
usually a small scale fluctuation is growing due to the strong Hubble expansion of H= 6·10 −6 m pl (see section 4.8.1)
and is affected by fluctuations. At horizon crossing the fluctuations freeze out and remain untouched until the scale
reaches the Hubble horizon again. Then the perturbations evolve according to cosmological perturbation theory, as it is
implemented incmbeasy. One might describe the generation of fluctuations of∆ R(k) by using a rather phenomenological
approach:
∆ R(l)=
� lhor+ε
l P
F(a, l)d ln l , (8.6)
where the function F(a, l)≥ 0 is a fluctuation generation function, which is a function of the length scale l. To parameterize
the ’time’, at which the fluctuation generation happens, F is also a function of the comoving scale k. The interpretation
of the integral is that a comoving scale k begins to grow from the Planck scale l P to the horizon scale l hor and a bit beyond.
During this growth the comoving scale collects fluctuation contributions on every extension, then freezes at the
horizon and remains unchanged until it enters the horizon again. The question comes up, what the properties of F(a, l)
are? The above consideration tells, that F(a, l)=0,∀λ