Instruments astronomiques - Université Lille 1

L. Duriez - Instruments astronomiques 30
pour cela le produit de convolution, qui correspond à la transformation :
f(t) ↦−→ g(ν) = 1 T
∫ +T/2
−T/2
f(t) exp(− √ −1νt)dt
où ν est une nouvelle variable ayant la dimension d’une fréquence (mais ce n’est pas ici la quantité c/λ ). En posant
a = A exp √ −1ϕ , on obtient par intégration l’expression :
g(ν) = a
sin((ω − ν)T/2)
(ω − ν)T/2
Cette fonction vaut a en ν = ω et tend vers zéro en oscillant lorsque ν s’éloigne de cette valeur :
1
sin(x)/x
(sin(x)/x)**2
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-20 -15 -10 -5 0 5 10 15 20
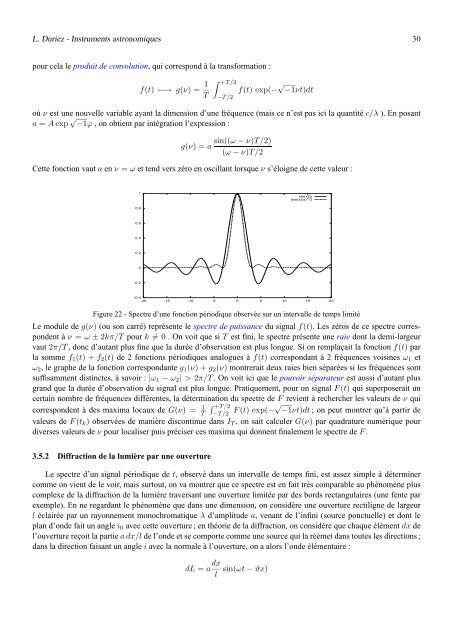
Figure 22 - Spectre d’une fonction périodique observée sur un intervalle de temps limité
Le module de g(ν) (ou son carré) représente le spectre de puissance du signal f(t). Les zéros de ce spectre correspondent
à ν = ω ± 2kπ/T pour k ≠ 0 . On voit que si T est fini, le spectre présente une raie dont la demi-largeur
vaut 2π/T , donc d’autant plus fine que la durée d’observation est plus longue. Si on remplaçait la fonction f(t) par
la somme f 1 (t) + f 2 (t) de 2 fonctions périodiques analogues à f(t) correspondant à 2 fréquences voisines ω 1 et
ω 2 , le graphe de la fonction correspondante g 1 (ν) + g 2 (ν) montrerait deux raies bien séparées si les fréquences sont
suffisamment distinctes, à savoir : |ω 1 − ω 2 | > 2π/T . On voit ici que le pouvoir séparateur est aussi d’autant plus
grand que la durée d’observation du signal est plus longue. Pratiquement, pour un signal F (t) qui superposerait un
certain nombre de fréquences différentes, la détermination du spectre de F revient à rechercher les valeurs de ν qui
∫ +T/2
−T/2
correspondent à des maxima locaux de G(ν) = 1 T
F (t) exp(−√ −1νt)dt ; on peut montrer qu’à partir de
valeurs de F (t k ) observées de manière discontinue dans I T , on sait calculer G(ν) par quadrature numérique pour
diverses valeurs de ν pour localiser puis préciser ces maxima qui donnent finalement le spectre de F .
3.5.2 Diffraction de la lumière par une ouverture
Le spectre d’un signal périodique de t, observé dans un intervalle de temps fini, est assez simple à déterminer
comme on vient de le voir, mais surtout, on va montrer que ce spectre est en fait très comparable au phénomène plus
complexe de la diffraction de la lumière traversant une ouverture limitée par des bords rectangulaires (une fente par
exemple). En ne regardant le phénomène que dans une dimension, on considère une ouverture rectiligne de largeur
l éclairée par un rayonnement monochromatique λ d’amplitude a, venant de l’infini (source ponctuelle) et dont le
plan d’onde fait un angle i 0 avec cette ouverture ; en théorie de la diffraction, on considère que chaque élément dx de
l’ouverture reçoit la partie a dx/l de l’onde et se comporte comme une source qui la réémet dans toutes les directions ;
dans la direction faisant un angle i avec la normale à l’ouverture, on a alors l’onde élémentaire :
dL = a dx l
sin(ωt − ϑx)