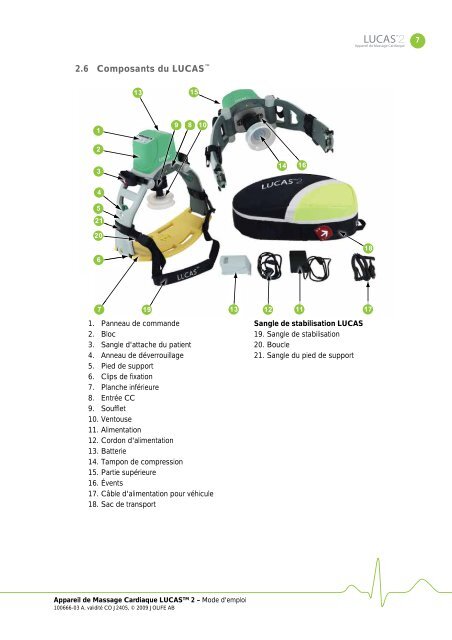
Mode d'emploi compression thoracique LUCAS 2 ... - Physio-Control

Y. Zhao et al. / J. Math. Anal. Appl. 331 (2007) 263–278 2692. If n 3 and p>(n+ 2)/(n − 2), then T = (θ, 1) for some θ ∈ (0, 1), andlim λ(d) =∞, limd→θ +λ(d) =∞. (2.8)d→1− We shall see later that Lemma 2.3 is the main reason that we can only show the exactS-shape for n 2, or n 3 and p (n + 2)/(n − 2). In the supercritical case when n 3(p >(n+ 2)/(n − 2)), there is a family of radial entire solutions of u + f(u)= 0onR n sothat 0 0 andthe one with k = 0 due to the translational perturbation u ↦→ u + k. Suppose that v(r,d) is thesolution of⎧⎨v ′′ + n − 1 v ′ + η ( v p − v p+1) = 0, r ∈ (0, 1),r(2.11)⎩v(r) > 0, v ′ (r) < 0, r ∈ (0, 1), v ′ (0) = v(1) = 0,which satisfies v(0) = d. From Lemma 2.1, η = η(d) is uniquely determined by d. For anyk ∈ (0,d), there exists a unique a = a(d,k) ∈ (0, 1) such that v(a,d) = k.Lemma 2.5. Let {v(r,d): d ∈ (0, 1)} be the solutions of (2.11), and let 0