Devoir commun de seconde Mathématiques

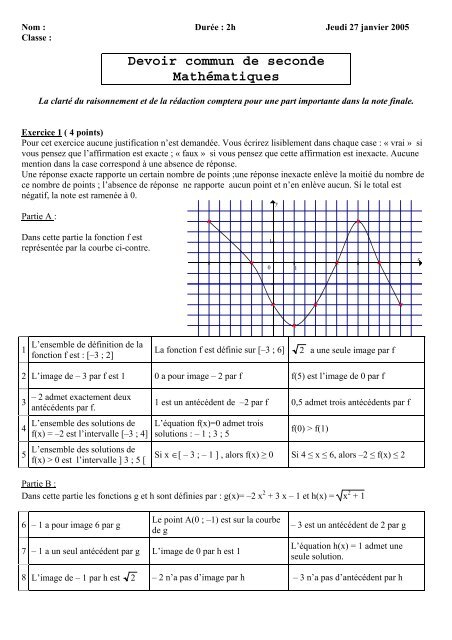
Nom :Classe :Durée : 2h Jeudi 27 janvier 2005Devoir commun de secondeMathématiquesLa clarté du raisonnement et de la rédaction comptera pour une part importante dans la note finale.Exercice 1 ( 4 points)Pour cet exercice aucune justification n’est demandée. Vous écrirez lisiblement dans chaque case : « vrai » sivous pensez que l’affirmation est exacte ; « faux » si vous pensez que cette affirmation est inexacte. Aucunemention dans la case correspond à une absence de réponse.Une réponse exacte rapporte un certain nombre de points ;une réponse inexacte enlève la moitié du nombre dece nombre de points ; l’absence de réponse ne rapporte aucun point et n’en enlève aucun. Si le total estnégatif, la note est ramenée à 0.Partie A :yDans cette partie la fonction f estreprésentée par la courbe ci-contre.10 1x1L’ensemble de définition de lafonction f est : [–3 ; 2]La fonction f est définie sur [–3 ; 6]2 a une seule image par f2 L’image de – 3 par f est 1 0 a pour image – 2 par f f(5) est l’image de 0 par f345– 2 admet exactement deuxantécédents par f.L’ensemble des solutions def(x) = –2 est l’intervalle [–3 ; 4]L’ensemble des solutions def(x) > 0 est l’intervalle ] 3 ; 5 [1 est un antécédent de –2 par f 0,5 admet trois antécédents par fL’équation f(x)=0 admet troissolutions : – 1 ; 3 ; 5f(0) > f(1)Si x ∈[ – 3 ; – 1 ] , alors f(x) ≥ 0 Si 4 ≤ x ≤ 6, alors –2 ≤ f(x) ≤ 2Partie B :Dans cette partie les fonctions g et h sont définies par : g(x)= –2 x 2 + 3 x – 1 et h(x) = x 2 + 16 – 1 a pour image 6 par gLe point A(0 ; –1) est sur la courbede g7 – 1 a un seul antécédent par g L’image de 0 par h est 1– 3 est un antécédent de 2 par gL’équation h(x) = 1 admet uneseule solution.8 L’image de – 1 par h est 2 – 2 n’a pas d’image par h – 3 n’a pas d’antécédent par h

Exercice 2 :(5 points)Soit f la fonction définie sur IR par f(x) = (x – 3) 2 – 2(x + 4)(3 – x)1) Développer f(x).2) Montrer que f(x) = (x – 3)(3x + 5).3) En choisissant la forme la plus adaptée, résoudre dans IR:a. f(x) = –15 .b. f(x) > 0.4) Soit la fonction g définie sur IR par g(x) = x 2 – 6x + 9.a. Factoriser g(x)b. Résoudre dans les inéquations : f(x) < g(x) et f(x)g(x) ≤ 3.Exercice 3 : (3,5 points)Soit un parallélogramme ABCD. On appelle I le milieu du segment [DC].1) Construire les points M et N définis par : AM = 3 AB et AN = 3 AD22) a- Démontrer que MN = – 3 2 AB + 3 AD et BI = – 1 AB + AD.23) b- En déduire que les droites (MN) et (BI) sont parallèles.4) a- Exprimer les vecteurs CM et CN en fonction des vecteurs AB et AD.b- En déduire que les points C , M et N sont alignés.Exercice 4 :( 4,5 points)[BC] et [DE] sont deux segments perpendiculairesd'intersection A .AB = 8 ; AD = 6; AC = 27 ; AE = 36 ( voir figure ci-contre)E1) Démontrer que les triangles ABE et ADC sont semblables.2) Les droites (CD) et (EB) se coupent en F .a) Démontrer que les triangles DFE et BFC sontsemblables.b) Montrer que : aire(DFE)aire(BFC) = 1,44 .3) a) Calculer les aires des triangles BCD et EBD.b) On note x l’aire du triangle BFD. Démontrer que x estsolution de l’équation : x + 168x + 105 = 1,44 .Calculer alors x .FBADCExercice 5 : (3 points)ABC désigne un triangle rectangle en A. On appelle P son périmètre et S son aire.On pose AB = x et AC = y et on suppose que x > y.1) On se propose de calculer l’hypoténuse h du triangle ABC en fonction de P et de S.a. Montrer que x + y = P – h et que h 2 + 4S=(x + y) 2( on pourra exprimer S en fonction de x et y ).b. En déduire que : h= P2 – 4S.2P2) Dans cette question, on suppose que P = 3 + 5 et S = 1 (l’unité est le cm) et on utilisera des résultats dela première question.a. Calculer h. On donnera le résultat sans racine carrée au dénominateur.b. Montrer que (x – y) 2 = 1.c. Calculer alors x et y.

La clarté du raisonnement et de la rédaction comptera pour une part importante dans la note finale.Exercice 1 ( 4 points)Pour cet exercice aucune justification n’est demandée. Vous écrirez lisiblement dans chaque case : « vrai » sivous pensez que l’affirmation est exacte ; « faux » si vous pensez que cette affirmation est inexacte. Aucunemention dans la case correspond à une absence de réponse.Une réponse exacte rapporte un certain nombre de points ;une réponse inexacte enlève la moitié du nombre dece nombre de points ; l’absence de réponse ne rapporte aucun point et n’en enlève aucun. Si le total estnégatif, la note est ramenée à 0.Partie A :yDans cette partie la fonction f estreprésentée par la courbe ci-contre.10 1x1L’ensemble de définition de lafonction f est : [–3 ; 2] FLa fonction f est définie sur [–3 ; 6]V2 a une seule image par fV2 L’image de – 3 par f est 1 F 0 a pour image – 2 par f V f(5) est l’image de 0 par f F345– 2 admet exactement deuxantécédents par f. FL’ensemble des solutions def(x) = –2 est l’intervalle [–3 ; 4]FL’ensemble des solutions def(x) > 0 est l’intervalle ] 3 ; 5 [F1 est un antécédent de –2 par fFL’équation f(x)=0 admet troissolutions : – 1 ; 3 ; 5VSi x ∈[ – 3 ; – 1 ] , alors f(x) ≥ 0V0,5 admet trois antécédents par fVf(0) > f(1)VSi 4 ≤ x ≤ 6, alors –2 ≤ f(x) ≤ 2VPartie B :Dans cette partie les fonctions g et h sont définies par : g(x)= – 2 x 2 + 3 x – 1 et h(x) = x 2 + 1678– 1 a pour image 6 par gV– 1 a un seul antécédent par gFL’image de – 1 par h est 2VLe point A(0 ; –1) est sur la courbede g VL’image de 0 par h est 1V– 2 n’a pas d’image par hF– 3 est un antécédent de 2 par gFL’équation h(x) = 1 admet uneseule solution. V– 3 n’a pas d’antécédent par hV

Exercice 2 :(5 points)1° f(x) = x 2 – 6 x + 9 – 2 (3 x – x 2 + 12 – 4 x) = x 2 – 6 x + 9 – 6 x + 2 x 2 – 24 + 8 x = 3 x 2 – 4 x – 15 .2° f(x) = (x – 3) 2 + 2 (x + 4) (x – 3) = (x – 3) ((x – 3) + 2 (x + 4))= (x – 3) (x – 3 + 2 x + 8)= (x – 3) (3 x + 5)3° a) f(x) = – 15 ⇔ 3 x 2 – 4 x – 15 = – 15⇔ 3 x 2 – 4 x = 0⇔ x (3 x – 4) = 0⇔ x = 0 ou x = 4 3S = ⎩⎪⎨ ⎪ ⎧0 , 4 3 ⎭⎪⎬ ⎪ ⎫b) f(x) > 0 ⇔ (x – 3) ( 3 x + 5) > 0.S = ] – ∞ , – 5/3 [ ∪ ] 3 , + ∞ [4° a) g(x) = (x – 3) 2b) f(x) < g(x) ⇔ (x – 3) (3 x + 5) < (x – 3) 2⇔ (x – 3) (3 x + 5) – (x – 3) 2 < 0⇔ (x – 3) [ (3 x + 5) – (x – 3)] < 0⇔ (x – 3) (2 x + 8) < 0S = ] – 4 , 3 [x – ∞ –5/3 3 + ∞x– 3 – 0 + + +3 x + 5 – – 0 +f(x) + 0 – 0 +x – ∞ – 4 3 + ∞x – 3 – – 0 +2 x + 8 – 0 + ++ 0 – 0 +c) f(x) (x – 3) (3 x + 5)< 3 ⇔g(x) (x – 3) 2 < 3⇔ 3 x + 5x – 3 – 3 < 0⇔3 x + 5 – 3 (x – 3)x – 3⇔ 1 4x – 3 < 0S = ] – ∞ , 3 [< 0x – ∞ 3 + ∞x – 3 – 0 ++ –NExercice 3 : (3,5 points)2° a) MN ⎯⎯→= MA ⎯⎯→+ AN ⎯⎯→= – 3 ⎯⎯→AB + 3 AD⎯⎯→2⎯⎯→BI = BA ⎯⎯→+ AD ⎯⎯→+ ⎯⎯→DI = – AB ⎯⎯→+ AD ⎯⎯→+ 1 2⎯⎯→DC = – AB ⎯⎯→+ AD ⎯⎯→+ 1 2⎯⎯→AB = – 1 2⎯⎯→AB + AD⎯⎯→DICb)⎯⎯→MN = 3 ⎯⎯→BI donc les vecteurs MN ⎯⎯→et ⎯⎯→BI sont colinéairesLes droites (MN) et (BI) sont donc parallèles.3° a) CM ⎯⎯→= CA ⎯⎯→+ AM ⎯⎯→= CB ⎯⎯→+ BA ⎯⎯→+ 3 2⎯⎯→AB= – AD ⎯⎯→– AB ⎯⎯→+ 3 2⎯⎯→AB = 1 2⎯⎯→AB – AD⎯⎯→ABM⎯⎯→CN = CA ⎯⎯→+ AN ⎯⎯→= – AC ⎯⎯→+ 3 AD ⎯⎯→= – AB ⎯⎯→– AD ⎯⎯→+ 3 AD ⎯⎯→= – AB ⎯⎯→+ 2 AD⎯⎯→b)⎯⎯→CN = – 2 CN. ⎯⎯→les vecteurs CM ⎯⎯→et CN ⎯⎯→sont colinéaires.Les points C, M et N sont donc alignés.

Exercice 4 : (4,5 points)1° ABE et ADC sont semblables :[DE] et [BC] sont perpendiculaires en A , donc on a : BAE = ADC (même mesure 90° ,ou angles opposés parle sommet) .ABAD = 8 6 = 4 AEet3 AC = 3627 = 4 ABdonc3 AD = AEAC .Les triangles ABE et ADC ont « un angle égal compris entre deux côtés respectivement proportionnels », ilssont donc semblables.2° a) DFE et BFC sont semblables :(EB) et (CD) se coupent en F , on a donc : DFE = CFBLes triangles ABE et ADC sont semblables(cf 1°) , leurs angles sont donc égaux deux à deux, d’où :AEB = ACD donc DEF = BCFLes triangles DFE et BFC ont alors deux angles égaux deux à deux , ils sont donc semblables.b) Rapport ds aires :Les triangles DFE et BFC sont semblables, les longueurs des côtés sont donc deux à deux proportionnelles.Soit k le rapport de similitude qui transforme le triangle BFC en DFE.On a k= DEBC .Calculons DE : A ∈ [DE] ,donc DE = AD + AE d’où DE = 6 + 36 = 42.Calculons BC : A ∈ [BC] ,donc BC = AB + AC d’où BC = 8 + 27 = 35.On obtient alors k = 4235 d’où k = 6 5 = 1,2.On peut alors écrire aire(DFE) = 1,2 2 aire(BFC), ou encore Aire(DFE)aire(BFC) =1,44.3°) a) aire(BCD) = BC×AD(8 + 27) × 6d’où aire(BCD) = d'où aire(BCD) = 105.22Aire(EBD) = ED×AB8 × (6 + 36)d’où aire(EBD) = d’où aire(EBD) = 168.22b) On note aire(BFD) = x.aire(BFC)=aire(BFD) + aire(BCD) d’où aire(BFC)=x + 105.Aire(DFE)=aire(BFD) + aire(BDE) d’où aire (DFE) = x + 168.On sait que : Aire(DFE)aire(BFC) = 1,44On a donc x + 168x + 105 = 1,44x > 0.x + 168=1,44 ⇔ x + 168 = 1,44 (x + 105)x + 105⇔ 0,44 x = 16,8⇔ x = 16,80,44⇔ x = 42011 .(x ≈ 38,18).

Exercice 5 : (3 points)1° a) P = x + y + h donc x + y = P – h.ABC rectangle en A donc h 2 = x 2 + y 2 et h 2 + 4 S = x 2 + y 2 + 4 × x y2 = x2 + y 2 + 2 x y = (x + y) 2b) h 2 + 4 S = (P – h) 2 donc h 2 + 4 S = P 2 – 2 P h + h 2 donc 2 P h = P 2 – 4 S donc h = P2 – 4 S2 P3° a) P = 3 + 5 et S = 1 donc h = (3 + 5 )2 – 4 × 12 × (3 + 5 )= 9 + 6 5 + 5 – 46 + 2 5= 10 + 6 56 + 2 5 = 5b) (x – y) 2 = x 2 + y 2 – 2 x y = h 2 – 2 × 2 × S = 5 – 4 = 1c) ‘x – y) 2 = 1 et x > y donc x – y = 1. On a : x + y = P – h = 3 + 5 – 5 = 3⎧ x – y = 1⎨⎩ x + y = 3 ⇔ x = 2⎩ ⎨⎧ y = 1