1° Fonction usuelle Fonction carrée 2 3 - Sylber-Maths

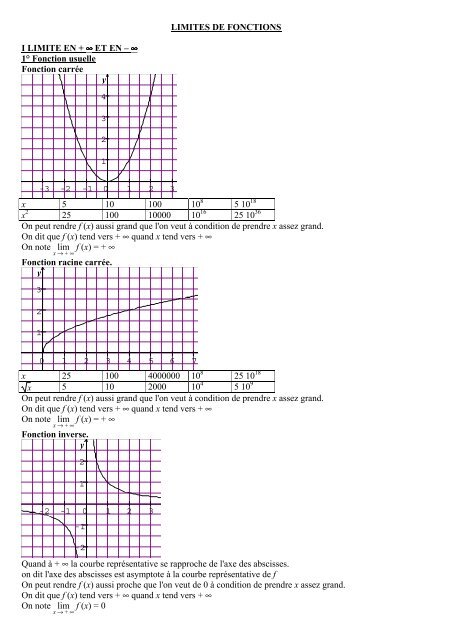
LIMITES DE FONCTIONSI LIMITE EN + ∞ ET EN – ∞1° Fonction usuelleFonction carréey4321-3-2-10 12 3x 5 10 100 10 8 5 10 18x 2 25 100 10000 10 16 25 10 36On peut rendre f (x) aussi grand que l'on veut à condition de prendre x assez grand.On dit que f (x) tend vers + ∞ quand x tend vers + ∞On note lim f (x) = + ∞x → + ∞Fonction racine carrée.y3210 12 3 4 5 6 7x 25 100 4000000 10 8 25 10 18x 5 10 2000 10 4 5 10 9On peut rendre f (x) aussi grand que l'on veut à condition de prendre x assez grand.On dit que f (x) tend vers + ∞ quand x tend vers + ∞On note lim f (x) = + ∞x → + ∞Fonction inverse.y21-2-10 12 3-1-2Quand à + ∞ la courbe représentative se rapproche de l'axe des abscisses.on dit l'axe des abscisses est asymptote à la courbe représentative de fOn peut rendre f (x) aussi proche que l'on veut de 0 à condition de prendre x assez grand.On dit que f (x) tend vers + ∞ quand x tend vers + ∞On note limx → + ∞ f (x) = 0

2° Limite finie en + ∞ et en – ∞ et asymptote horizontaleSoit f une fonction définie sur un intervalle IIntuitivement, dire que f a pour limite L en + ∞ , signifie que lorsque x prend des valeurs de plus en plusgrandes vers + ∞ , les nombres f (x) viennent s’accumuler autour de L .On note : limx → +∞ f ( x ) = LOn dit que la droite d’équation y = L est asymptote horizontale à la courbe Cf en + ∞ .Lf ( x )Cf⎯→j3° Limite infinie en + ∞ et en – ∞Soit f une fonction définie sur un intervalle [ a ; + ∞ [Si « f ( x ) est aussi grand que l’on veut dès que x est assez grand » , on dit que f a pour limite + ∞ en + ∞ et onnote :lim f (x) = + ∞x → + ∞CfO⎯→ix⎯→jO⎯→iOn dit aussi que la fonction f tend vers + ∞ quand x tend vers + ∞ .Remarques :Une fonction n’a pas forcément une limite finie ou infinie quand x tend vers + ∞ .( Par exemple x ⏐⎯⎯→ sin x , x ⏐⎯⎯→ cos x … )On définit de la même façon …limx → + ∞ f (x) = – ∞lim f (x) = – ∞x → – ∞lim f (x) = + ∞x → – ∞O⎯→j⎯→iCf⎯→jO⎯→iCfCfDans ces deux cas, f est définie sur un intervalle de la forme O ]-∞ ; b ]4° Asymptote obliqueSoit C la courbe représentant une fonction f dans un repère.Dire que la droite d’équation y = a x + b est asymptote oblique à C en + ∞ revient à dire que :lim [ f (x) – (a x + b) ] = 0yx → + ∞NExemplef (x) = 2 x2 – 1f ( x )CMx + 1⎯→j⎯→ix

5° limite des fonctions usuelles1limx → + ∞ x = 01limx → – ∞ x = 0limx → + ∞1x 2 = 0lim 1x → – ∞ x 2 = 01limx → + ∞ x 3 = 01limx → – ∞ x 3 = 0limx → + ∞limx → – ∞1x = 01x = 0lim x = + ∞x → + ∞lim x = – ∞x → – ∞limx → + ∞ x2 = + ∞limx → – ∞ x2 = + ∞limx → + ∞ x3 = + ∞limx → – ∞ x3 = – ∞limx → + ∞x = + ∞II LIMITE EN a1° Limite infinie en a et asymptote verticaleSoit f une fonctionSi « f ( x) est aussi grand que l’on veut dès que x est assez proche de a » , on dit que f a pour limite + ∞ en a eton note :xlim→ a f ( x ) = + ∞CfOn définit de la même façonxlim→ a f ( x ) = – ∞On dit que la droite d’équation x = a est asymptote verticale à la courbe Cf2° limite des fonctions usuelleslimx → 0 + x = + ∞ , lim x → 0 + x²limx → 0 – x = – ∞ , lim x → 0 – x²Les courbes représentant ces3° Limite finie en aExemples : lim sin (2 x +x → 4III OPERATION SUR LESLes théorèmes qui suivent,Pour la plupart d’entre euxPar convention et pour simplifierOn note lim f et lim g lesx → α x → αOn note par un point d’interrogationformes indéterminées . Ces1° Limite de k flim x → αlim k f (x) ( avec k > 0 )x → αlim x → αen+ ∞∞ ,fonctions= sinLIMITESprésentéssont:limites denécessiteront k l = +– ∞admettent l’axelim→ 1de tableaumais …toutesil n’yune étude + ∞ + ∞commemath,, engénérale.chaque fois – ∞OasymptotequelquesenOn ditseaverticalecasqu’ilprésenteront.0= , lim1x → 0 + x 3 ∞ , limx → 0 + x == + limx → 0 – x 3 =des ordonnées .4) 12 ,xx² + 3 = 2sous forme sont admis., ils naturels comme souvent en il y a particuliers.f et de g , les deux en α fini + ∞ ou - ∞les cas où a pas de conclusion s’agit de cas decas particulière qu’ils

Exemple : Soit la fonction g définie sur IR * par g : x ⏐⎯⎯→ – 2 x²lim g(x) = 0 , lim g(x) = 0 , lim g(x) = - ∞ et limx → – ∞ x → + ∞ +x → 0g(x) = – ∞x → 0 –2° Limite de f + gSi lim x → α l l l + ∞ – ∞ + ∞et lim x → α l ' + ∞ – ∞ + ∞ – ∞ – ∞limx → α(f (x) + g(x)) l + l ' + ∞ – ∞ + ∞ – ∞Exemple : Soit la fonction h définie sur IR+ * par h : x ⏐⎯⎯→ x – 2 x².On a h = f + g avec f : x ⏐⎯⎯→ x et g : x ⏐⎯⎯→ – 2 x²On sait que lim f ( x ) = + ∞ et lim g ( x ) = 0 ;x → + ∞ x → + ∞donc lim h ( x ) = + ∞x → + ∞3° Limite de f × gSi lim f (x) =x → αl l ≠ 0 + ∞ ou – ∞ 0et limx → αlimx → αg(x) = l ' + ∞ ou – ∞ + ∞ ou – ∞ + ∞ ou – ∞(f (x) × g(x)) l × l ' ∞ signe à déterminer ∞ signe à déterminer Forme indéterminéeExemple : Soit la fonction h définie sur IR+ par h : x ( x + 2 ) x⏐⎯⎯→On a h = f × g avec f : x x + 2 et g : x x⏐⎯⎯→ ⏐⎯⎯→On sait quexlim→ 0 f ( x ) = 2 et x lim → 0x = 0 ; doncxlim→ 0 h ( x ) = 04° Limite de f gCas où la limite de g n’est pas nulle Cas où la limite de g est nulleSi lim x → α l l l ≠ 0 ∞ ∞ + ∞ 0et lim x → αl ' ≠ 0 + ∞ 0 l ' ≠ 0 0 + ∞ 0limx → αf (x)g(x)ll '0∞signe à déterminerExemple : Soit la fonction h définie sur IR+ * par h : xOn a h = f g ou f : x ⏐⎯⎯→ 2 x – 4 et g : x ⏐⎯⎯→ x⏐⎯⎯→2x – 4xForme indéterminéeOn sait que lim f ( x ) = – 4 et lim g ( x ) = 0+ ; d’où lim h ( x ) = – ∞+ +x → 0 x → 0 x → 0 +