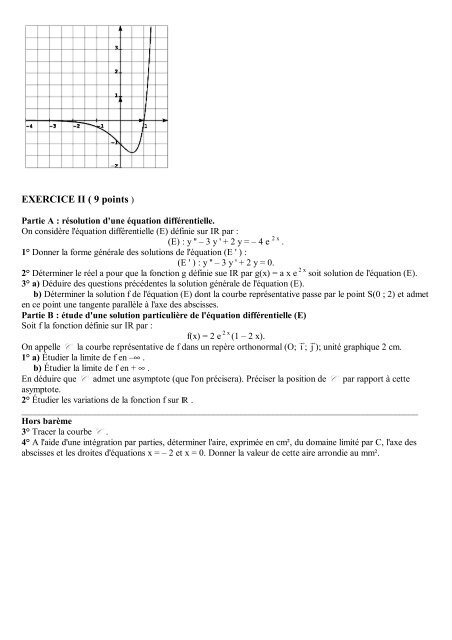
EXERCICE I ( 11 points )

More documents

Recommendations

Info

<strong>EXERCICE</strong> II ( 9 <strong>points</strong> )Partie A : résolution d'une équation différentielle.On considère l'équation différentielle (E) définie sur IR par :(E) : y '' – 3 y ' + 2 y = – 4 e 2 x .1° Donner la forme générale des solutions de l'équation (E ' ) :(E ' ) : y '' – 3 y ' + 2 y = 0.2° Déterminer le réel a pour que la fonction g définie sue IR par g(x) = a x e 2 x soit solution de l'équation (E).3° a) Déduire des questions précédentes la solution générale de l'équation (E).b) Déterminer la solution f de l'équation (E) dont la courbe représentative passe par le point S(0 ; 2) et admeten ce point une tangente parallèle à l'axe des abscisses.Partie B : étude d'une solution particulière de l'équation différentielle (E)Soit f la fonction définie sur IR par :f(x) = 2 e 2 x (1 – 2 x).On appelle C la courbe représentative de f dans un repère orthonormal (O; ⎯→ i ; ⎯→ j ); unité graphique 2 cm.1° a) Étudier la limite de f en –∞ .b) Étudier la limite de f en + ∞ .En déduire que C admet une asymptote (que l'on précisera). Préciser la position de C par rapport à cetteasymptote.2° Étudier les variations de la fonction f sur IR ._______________________________________________________________________________________Hors barème3° Tracer la courbe C .4° A l'aide d'une intégration par parties, déterminer l'aire, exprimée en cm², du domaine limité par C, l'axe desabscisses et les droites d'équations x = – 2 et x = 0. Donner la valeur de cette aire arrondie au mm².
A 1° y' – 2 y = 0 ⇔ y'x= 2. Solutions de la forme : x ⏐⎯⎯→ k e2y2° h(x) = x e 2 x et h '(x) = e 2x + 2 x e 2x h'(x) – 2 h(x) = e 2x + 2 x e 2x – 2 x e 2 x = e 2 xh est bien une solution particulière de l'équation différentielle (E).3° les solutions sont de la forme : x ⏐⎯⎯→ x e2 x + k e 2 x4° f(x) = x e 2 x + k e 2 x . f(0) = – 1 ⇔ 0 × e 2 × 0 + k e 2 × 0 = – 1 ⇔ k = – 1 et donc f(x) = x e 2 x – e 2 x = (x – 1) e 2xB 1° a) f(x) = x e 2 x – e 2 x . On a : lim x – 1 = + ∞ et limx → +∞ x → +∞ e2 x = + ∞ donc lim f(x) = + ∞ .x → +∞b) limx → –∞ x e2x = 0 et limx → –∞ e2x = 0 donc limx → –∞ f(x) = 0c) la droite d'équation ' y = 0" est asymptote à – ∞ à C .2° a)u (x) = x – 1 et u '(x) = 1v(x) = e 2 x et v'(x) = 2 e 2 x donc f '(x) = 1 × e2 x + (x – 1) × 2 e 2 x = (1 + 2 x – 2) e 2 x = (2 x – 1) e 2 x⎪⎫⎬⎭⎪b) f (x) ≥ 0 ⇔ 2 x – 1 ≥ 0 ⇔ x ≥ 1 2c)3° a) e t = 1 + t + t2 2 + t3 6 + t ε 1(t)e 2 x = 1 + 2 x +(2 x)22+(2 x)36(e 2 x > 0)+ x ε 2 (x) = 1 + 2 x + 2 x 2 + 4 x33 + x ε 3 (x)f(x) = (x – 1) × (1 + 2 x + 2 x 2 + 4 x33 + x ε 3 (x)) = x + 2 x 2 + 2 x 3 – 1 – 2 x – 2 x 2 – 4 x33 + x ε 4 (x)= – 1 – x + 2 3 x3 + x 3 ε 4 (x)c) Equation tangente : " y = – 1 – x "23 x3 est du signe de x donc pour x voisin de 0 on a C au dessous de T avant 0 puis C au dessus de Tx 02– +3 x3 C au dessous C au dessusde TC 1° I (α) = ⌡ ⌠ 0(x – 1) e 2 x dxαu(x) = x – 1 et u '(x) = 1 ⎪ ⎫⎬v '(x) = e 2 x et v(x) = e2 x2 ⎭⎪0de Tintégration par partie :I (α) = ⎢ ⎡ (x – 1) e2 x⎣ 2 ⎦ ⎥⎤ – ⎮ ⌠ α e 2 xα ⌡ 02 dx= (0 – 1) e02 – α – 1 e 2 α –2⎢ ⎡ e 2 x 0⎣ 4 ⎦ ⎥⎤ = – 1α 2 – α 2 e2 α + e2 α2 – 1 4 + e2 α4= – 3 4 – α 2 e2 α + 3 e2 α= – 3 4 4 – ⎝ ⎜⎛ 12 α – 3 4⎠ ⎟⎞ e2 α2° a) lim α e2 α = lim e2 α = 0 donc lim – 3α → –∞ α → –∞ α → –∞ 4 – α 2 e2 α + 3 e2 α= – 3 4 4x −∞ 1/2 +∞signe de f ' – 0 +0 + ∞f– e/2b) – 3 4représente, en unité d'aire, l'aire de la partie du plan limité par : la droite d'équation " x = 0 ", la courbeC et la tangente T .
Page 1: BTS MAI 1 Devoir surveillé n°7 Ma

EXERCICE I ( 11 points )

Create successful ePaper yourself

Delete template?

Save as template?