621 Devoir surveillé n° 4 Mercredi 6 octobre 2010 x f4 (x) = 1 2 x – x ...

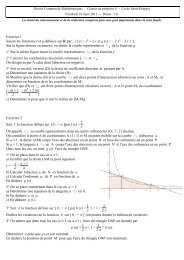
Exercice 1 : 10 pointsPour chacune des fonctions suivantes calculer la fonction dérivée en précisant son ensemble de définition.f 1 (x) = – 3 x 4 + 2 x 2 + 3 – 1 xf 1 est la somme d'un polynôme avec la fonction inverse donc f 1 est dérivable sur IR *Pour tout réel x 0, f 1 (x) = – 12 x 3 + 4 x + 1 x 2f 2 (x) = 3 x + 1x – 2 .f 2 est une fonction rationnelle (quotient de deux polynômes) donc f 2 est dérivable sur son ensemble de définition c'est à dire surIR – { 2 }Pour tout réel x 2, f 2 (x) = u (x)v (x) avec u (x) = 3 x + 1 et u '(x) = 33 (x – 2) – (3 x + 1) × 1 donc f v (x) = x – 2 et v '(x) = 11 (x) =(x – 2) 2 = –1f 3 (x) =2 x 2 + 1f 3 est une fonction rationnelle donc f 3 est dérivable sur son ensemble de définition c'est à dire sur IR – { 2 }Pour tout réel x on a : f 3 (x) =f 3 (x) = –u '(x)(u (x) 2 ) = – 4 x(2 x 2 + 1) 27(x – 2) 21u (x) avec u (x) = 2 x2 + 1, u dérivable sur IR et u '(x) = 4 x donc f 3 est dérivable sur IR et,f 4 (x) = 12 x – x 2f 4 est une fonction rationnelle donc f 4 est dérivable sur son ensemble de définition c'est à dire sur IR – { 0 }Pour tout réel x 0, f 4 (x) = 1 2 × 1 x – 1 2 × x donc f 4'(x) = 1 2 × – 1x 2 – 1 2 × 1 = – 12 x 2 – 1 2 = – 1 – x22 x 2 f 5 (x) =(3 x + 1) 3 :f 5 est un polynôme donc f 5 est dérivable sur IRPour tout réel x, f 5 (x) = (a x + b) 3 avec a x + b = 3 x + 1 donc f 5 '(x) = 3 (a x + b) 2 × a = 3 (3 x + 1) 2 × 3 = 9 (3 x + 1) 2f 6 (x) = 3 x2 – 1x 2 + 3 xf 6 est une fonction rationnelle donc }Pour tout réel x IR – { – 3 ; 0 } on a :f 6 (x) = u (x)v (x) avec u (x) = 3 x2 – 1, u dérivable sur IR et u '(x) = 6 xv (x) = x 2 + 3 x, v dérivable sur IR et v '(x) = 2 x + 3 donc f 6 est dérivable sur son ensemble dedéfinition c'est à dire sur IR – { – 3 ; 0 } et f 6 '(x) = 6 x (x2 + 3 x) – (3 x 2 – 1) (2 x + 3)(x 2 + 3 x) 2 = 6 x3 + 18 x 2 – 6 x 3 – 9 x 2 + 2 x + 3(x 2 + 3 x) 2 =9 x 2 + 2 x + 3(x 2 + 3 x) 2f 7 = (x + 1) x = u (x) v (x) avec u définie et dérivable sur IR et v définie sur [ 0 ; + [, dérivable sur ] 0 ; + [ donc f 7 estdérivable sur ] 0 ; + [ et, pour tout réel x > 0 on a : u (x) = x + 1 et u '(x) = 111v (x) = x et v '(x) = donc f 7 '(x) = 1 × x + (x + 1) ×2 x2 x = x × 2 x+ x + 12 x x = 2 x + x + 1 = 3 x + 12 x 2 xf 8 = 2 x + 1x + 1= u (x)v (x)u est définie sur [ 0 ; + [ et dérivable sur ] 0 ; + [v est définie et dérivable sur IRv (x) = 0 si, et seulement si, x = – 1 et – 1 ] 0 ; + [ donc f 8 est définie sur [ 0 ; + [ et f 8 dérivable sur ] 0 ; + [Pour tout réel x, > 0 on a :1 u (x) = 2 x + 1 et u '(x) = 2 ×2 x = 1 1x + 1× (x + 1) – (2 x + 1) × 1x x – 2 x + xxx donc f 8 '(x) =(x + 1)2 =(x + 1) 2v (x) = x + 1 et v '(x) = 1