Exercice 1

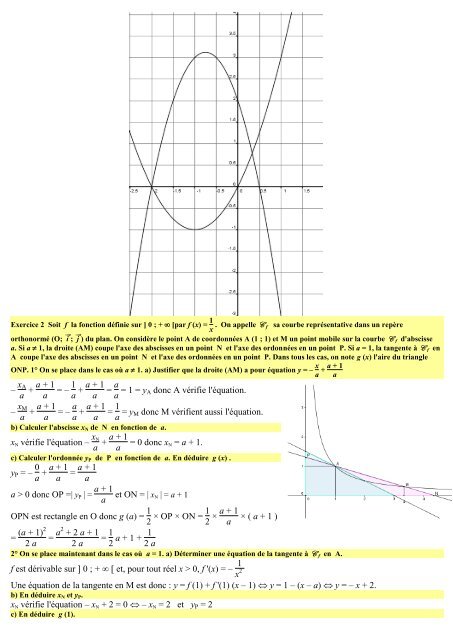
Exercice 2 Soit f la fonction définie sur ] 0 ; + [par f (x) = 1 x . On appelle C f sa courbe représentative dans un repèreorthonormé (O; i ; j ) du plan. On considère le point A de coordonnées A (1 ; 1) et M un point mobile sur la courbe C f d'abscissea. Si a 1, la droite (AM) coupe l'axe des abscisses en un point N et l'axe des ordonnées en un point P. Si a = 1, la tangente à C f enA coupe l'axe des abscisses en un point N et l'axe des ordonnées en un point P. Dans tous les cas, on note g (x) l'aire du triangleONP. 1° On se place dans le cas où a 1. a) Justifier que la droite (AM) a pour équation y = – x a + a + 1a– x Aa + a + 1 = – 1 a a + a + 1 = a a a = 1 = y A donc A vérifie l'équation.– x Ma + a + 1 = – a a a + a + 1 = 1 a a = y M donc M vérifient aussi l'équation.b) Calculer l'abscisse x N de N en fonction de a.x N vérifie l'équation – x Na + a + 1 = 0 donc xaN = a + 1.c) Calculer l'ordonnée y P de P en fonction de a. En déduire g (x) .y P = – 0 a + a + 1a= a + 1aa > 0 donc OP =| y P | = a + 1aet ON = | x N | = a + 1OPN est rectangle en O donc g (a) = 1 2 × OP × ON = 1 2 × a + 1 × ( a + 1 )a(a + 1)2= = a2 + 2 a + 1= 1 2 a 2 a 2 a + 1 + 12 a2° On se place maintenant dans le cas où a = 1. a) Déterminer une équation de la tangente à C f en A.f est dérivable sur ] 0 ; + [ et, pour tout réel x > 0, f '(x) = – 1x 2Une équation de la tangente en M est donc : y = f (1) + f '(1) (x – 1) y = 1 – (x – a) y = – x + 2.b) En déduire x N et y P .x N vérifie l'équation – x N + 2 = 0 – x N = 2 et y P = 2c) En déduire g (1).