IMPALCATO A GRATICCIO

Metodo di ripartizione dei carichi: Guyon - Massonnet - Bareš 

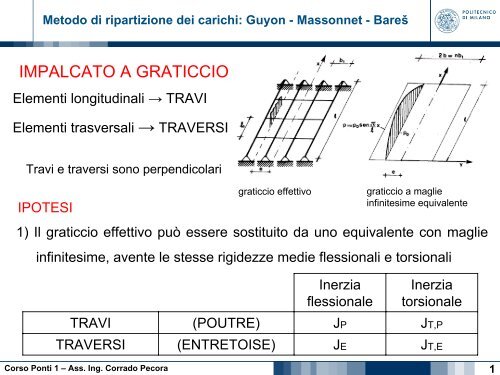
IMPALCATO A GRATICCIO 

Elementi longitudinali → TRAVI 

Elementi trasversali → TRAVERSI 

Travi e traversi sono perpendicolari 

IPOTESI 

Corso Ponti 1 – Ass. Ing. Corrado Pecora 

graticcio effettivo graticcio a maglie 

infinitesime equivalente 

1) Il graticcio effettivo può essere sostituito da uno equivalente con maglie 

infinitesime, avente le stesse rigidezze medie flessionali e torsionali 

Inerzia 

flessionale 

Inerzia 

torsionale 

TRAVI (POUTRE) JP JT,P 

TRAVERSI (ENTRETOISE) JE JT,E 

1


2) L’impalcato si ritiene appoggiato sui bordi estremi (x=0 e x=L) e libero 

sugli altri due (y=-b e y=b) 

Analisi armonica nella direzione x 

Sviluppo in serie troncato al 1° termine 

→ errore ~ 2% 

3) La ripartizione dei carichi fra le travi longitudinali (ripartizione trasversale), 

per ogni condizione di carico, è la stessa che si avrebbe se i carichi 

fossero distribuiti in senso longitudinale con legge (sinusoidale) 


2


COEFFICIENTE DI RIPARTIZIONE TRASVERSALE 

- carico agente su una parallela all’asse x con eccentricità “e” 

- carico ripartito con legge sinusoidale 

- ipotesi di vincolo già descritte 

la deformata ha forma di semionda di sinusoide 

w(x,y) = w(y,e) sen(πx/L) 

nel caso di carico sinusoidale ripartito su tutta la larghezza 2b dell’impalcato 

p0(x) = p(x)/2b = p1 sen(πx/L)/2b 

la deformata si presenta cilindrica w0(x) = w0 sen(πx/L) 

il rapporto k(y,e) = w(x,y)/w 0(x) = w(y,e)/w 0 è detto coefficiente di ripartizione 

trasversale e consente di valutare la distribuzione delle sollecitazioni prodotte 

dall’azione dei carichi sull’impalcato 


3


trave carico 

k(y,e) è indipendente dall’ascissa x 

k(y,e) = k(e,y) TEOREMA DI MAXWELL 

Tale parametro dipende da: 

1) il parametro di irrigidimento 

ϑ

K0 

K1 


Massonnet per evitare di valutare k α per ogni valore di α ha 

fornito la seguente relazione semiempirica 

k 

k 

k 

k 


α 

0 

1 

= 

→ 

→ 

k 

0 

k 

+ 

( k − k ) 

per 

per 

1 

α 

α 

0 

= 

0 

= 1 

⋅ 

α 

rigidezza 

piastra 

torsionale 

isotropa 

Metodo caratterizzato dall’uso di tabelle 

y/e -1,00 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00 

-1,00 4,6376 3,4626 2,3904 1,4672 0,6944 0,0460 -0,5170 -1,0350 -1,5388 

-0,75 3,4626 2,7877 2,1034 1,4522 0,8625 0,3358 -0,1425 -0,5933 -1,0350 

-0,50 2,3904 2,1034 1,7920 1,4214 1,0223 0,6237 0,2359 -0,1425 -0,5170 

-0,25 1,4672 1,4522 1,4214 1,3348 1,1509 0,9019 0,6237 0,3358 0,0460 

0,00 0,6944 0,8625 1,0223 1,1509 1,2064 1,1509 1,0223 0,8625 0,6944 

0,25 0,0460 0,3358 0,6237 0,9019 1,1509 1,3348 1,4214 1,4522 1,4672 

0,50 -0,5170 -0,1425 0,2359 0,6237 1,0223 1,4214 1,7920 2,1034 2,3904 

0,75 -1,0350 -0,5933 -0,1425 0,3358 0,8625 1,4522 2,1034 2,7877 3,4626 

1,00 -1,5388 -1,0350 -0,5170 0,0460 0,6944 1,4672 2,3904 3,4626 4,6376 

y/e -1,00 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00 

-1,00 2,0184 1,6715 1,3586 1,0943 0,8814 0,7158 0,5902 0,4944 0,4157 

-0,75 1,6715 1,5147 1,3215 1,1208 0,9392 0,7875 0,6670 0,5727 0,4944 

-0,50 1,3586 1,3215 1,2594 1,1425 1,0031 0,8708 0,7583 0,6670 0,5902 

-0,25 1,0943 1,1208 1,1425 1,1339 1,0646 0,9671 0,8708 0,7875 0,7158 

0,00 0,8814 0,9392 1,0031 1,0646 1,0957 1,0646 1,0031 0,9392 0,8814 

0,25 0,7158 0,7875 0,8708 0,9671 1,0646 1,1339 1,1425 1,1208 1,0943 

0,50 0,5902 0,6670 0,7583 0,8708 1,0031 1,1425 1,2594 1,3215 1,3586 

0,75 0,4944 0,5727 0,6670 0,7875 0,9392 1,1208 1,3215 1,5147 1,6715 

1,00 0,4157 0,4944 0,5902 0,7158 0,8814 1,0943 1,3586 1,6715 2,0184 

kα 

5,0000 

4,0000 

3,0000 

2,0000 

1,0000 

0,0000 

-1,0000 

-2,0000 

-1,00 

nulla 

(GUYON) 

-0,50 

θ = 0,46900 

0,00 

y/b 

0,50 

α = 0,03929 

1,00 

e/b=-1.00 

e/b=-0.75 

e/b=-0.50 

e/b=-0.25 

e/b=+0.00 

e/b=+0.25 

e/b=+0.50 

e/b=+0.75 

e/b=+1.00 

5

M 

M 

M 

M 


Momento flettente nella trave 

∑ 

i α 

i= 

1 

x = Mmedio 

⋅ n 

y 

xy 

yx 

= b ⋅ 

n 

∑ 

i= 

1 

p 

= −2 

⋅ 

γ 

= −2 

⋅ 

γ 

i 

P 

P 

n 

⋅μ 

α 

γP 

+ γ 

γE 

+ γ 

p ⋅k 

∑ 

i= 

1 

( y, 

e ) 


p 

Momento flettente nel traverso 

( y, 

e ) 

Momento torcente nella trave 

E 

E 

i 

⋅b 

⋅ 

⋅b 

⋅ 

i 

n 

∑ 

i= 

1 

n 

∑ 

i= 

1 

p 

p 

i 

i 

i 

⋅ τα 

⋅ τα 

( y, 

e ) 

Momento torcente nel traverso 

Riepilogo delle principali relazioni 

( y, 

e ) 

i 

i 

Taglio nella trave 

V 

x 

= V 

x medio 

∑ 

i= 

1 

⋅ 

n 

∑ 

i= 

1 

α 

p 

i 

⋅k 

α( 

y, 

ei) 

γ 

+ 

n 

ρ 

p 

∑ 

i= 

1 

Taglio nel traverso 

V 

y 

= 

n 

p 

i 

⋅ κ 

( y, 

e 

i 

i 

2 ⋅ γ P ) + 

γ + γ 

P 

E 

E 

E 

π 

⋅b 

⋅ ⋅ 

l 

π 

⋅ b ⋅ ⋅ 

l 

n 

∑ 

i= 

1 

n 

p 

∑ 

i= 

1 

i 

⋅μ 

p 

i 

α 

⋅ τ 

( y, 

e ) 

α 

i 

( y, 

e 

i 

) 

6



Esempio numerico 

Determinare gli effetti della ripartizione trasversale con il 

metodo di Massonnet, valutando i momenti flettenti e 

torcenti e i tagli nelle travi e nei traversi 

7


Valutare α e ϑ 

ϑ 

= 


b 

L 

4 

ρ 

ρ 

P 

E 

α 

= 

γ 

P 

+ γ 

P 

E 

2 ρ ⋅ρ 

E 

L=22.30m 

2b = 11.50m 

b 1 = 1.00m 

Momento 

d’inerzia 

flessionale 

8


In genere il problema legato alla determinazione dell’inerzia torsionale non è 

dato dalla determinazione di β (che si può assumere pari a 1/3), quanto dalla 

trasformazione dei rettangoli in aree equivalenti in modo da ricondursi in 

sezioni a o T, in cui il flusso delle tensioni tangenziali è noto. 


3 

J β a s = 

T, 

P = ∑ 

k= 

1 

k 

k 

3 

k 

520241, 

66 

cm 

4 

Momento 

d’inerzia 

torsionale 

9


Rigidezza torsionale per sezioni composte da rettangoli allungati 


10


SEZIONE COMPOSTA DA 3 RETTANGOLI 

GEOMETRIA 

nr. Base [m] Altezza [m] 

1 4,000 0,200 

2 0,200 1,000 

3 2,000 0,300 

INERZIA FLESSIONALE 

A = 1,60000 m^2 area 

Sx = 1,03000 m^3 momento statico 

xG = 0,000 m ascissa baricentro 

yG = 0,644 m ordinata baricentro 

Ix = 1,22333 m^4 inerzia flessionale asse xx 

IxG = 0,56027 m^4 inerzia flessionale asse GG 

INERZIA TORSIONALE 

Geometria per calcolo inerzia torsionale 

nr. sk [m] ak [m] betak 

1 0,200 4,000 0,3229 

2 0,200 1,000 0,2915 

3 0,300 2,000 0,3020 

Jt = 0,02897 m^4 inerzia torsionale 

3 

∑ 

k = 1 

J = β 

⋅ s 


t 

k 

3 

k 

⋅ a 

k 

4,500 

4,000 

3,500 

3,000 

2,500 

2,000 

1,500 

1,000 

0,500 

0,000 

-2,500 

-2,000 

-1,500 

-1,000 

-0,500 

0,000 

0,500 

1,000 

1,500 

2,000 

2,500 

Rettangolo 1 

Rettangolo 2 

Rettangolo 3 

Baricentro 

11


DM 2008 

EC2 

Shear lag Airy 


12



2 

J β a s = 

T, 

E = ∑ 

k= 

1 

k 

k 

3 

k 

1433053, 

33 

cm 

4 

Momento 

d’inerzia 

flessionale 

Momento 

d’inerzia 

torsionale 

13



14


Momento flettente nella trave 

1) Sviluppo in serie di Fourier del carico 

2) Calcolo delle sollecitazioni (M x) relative 

ad ogni condizione di carico 

3) Definizione ed uso della funzione k α 

4) Calcolo di M x sull’impalcato 

Normativa di riferimento 


x 

∑ 

⋅k 

i 

i= 

1 = Mmedio 

⋅ n 

D. M. LL. PP. 4/5/1990 “Aggiornamento delle norme tecniche per la 

progettazione, la esecuzione e il collaudo dei ponti stradali” 

Differenze con D. M. 2008: carichi mobili, coefficiente dinamico, larghezza corsia 3,50m 

M 

n 

p 

∑ 

i= 

1 

α 

p 

( y, 

i 

e 

i 

) 

15




2) Calcolo delle sollecitazioni (M x ) relative ad 

ogni condizione di carico 

3) Definizione della funzione k α 


16



17



18



M(x) 

3500,0 

3000,0 

2500,0 

2000,0 

150 0 ,0 

10 0 0 ,0 

500,0 

0,0 

0,0 

-500,0 

5,0 10,0 15,0 20,0 25,0 

x 

M_Fourier 

M_effettivo 

M_corretto 

19




2) Calcolo delle sollecitazioni (M x ) relative 

ad ogni condizione di carico 



20



L=22,30m 

NORMATIVA 

21








22


K0 

K1 

K 

kα 

5,0000 

4,0000 

3,0000 

2,0000 

1,0000 

0,0000 

-1,0000 

-2,0000 

-1,00 


-0,50 

θ = 0,46900 α = 0,03929 

e/y -1,00 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00 

1,00 -1,5388 -1,0350 -0,5170 0,0460 0,6944 1,4672 2,3904 3,4626 4,6376 

e/y -1,00 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00 

1,00 0,4157 0,4944 0,5902 0,7158 0,8814 1,0943 1,3586 1,6715 2,0184 

= K 

+ 

( K − K ) ⋅ α 

α 0 1 0 

e/y -1,00 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00 

1,00 -1,1514 -0,7319 -0,2976 0,1788 0,7315 1,3933 2,1859 3,1076 4,1184 

Fissata 

l’ordinata y, 

ossia la 

trave 

longitudinale 

Larghezza 

impalcato 

(y/b) 

0,00 

0,50 

1,00 

TABELLE 

BIBLIOGRAFIA 

Le calcul des grillages 

de poutres et dalles 

orthotropes 

23








24


Utilizzo della funzione k α 

quale linea di influenza 


25

M 


∑ 

i α 

i= 

1 

x = Mmedio 

⋅ n 

n 

p ⋅k 

∑ 

i= 

1 

11 travi 

( y, 

e ) 

(162.2419+324.4838 

+43.5129)/11 = 

48.2035 


p 

i 

i 

26



27



28



Momento flettente nel traverso 

M 

y 

= b ⋅ 

n 

∑ 

i= 

1 

p 

i 

⋅μ 

α 

( y, 

( μ − μ ) ⋅ α 

μ α = μ 0 

+ 1 0 

e 

i 

) 

29



30



Momento torcente nella trave 

M 

xy 

= −2 

⋅ 

γ 

P 

γ 

+ 

P 

γ 

E 

⋅b 

⋅ 

n 

∑ 

i= 

1 

p 

α=0 

i 

⋅ τα 

( 

y, 

rigidezza torsionale 

nulla 

e 

i 

) 

31



32



Momento torcente nel traverso 

M 

yx 

= −2 

⋅ 

γ 

P 

γ 

+ 

E 

γ 

E 

⋅b 

⋅ 

n 

∑ 

i= 

1 

p 

i 

⋅ τα 

( 

y, 

e 

i 

) 

33



V 

x 

= V 

Taglio nella trave 

x medio 

⋅ 

n 

∑ 

i= 

1 

p 

⋅k 

α( 

y, 

ei 

) 

γ 

+ 

n 

ρ 

p 

i 

∑ 

i= 

1 

i 

E 

E 

π 

⋅b 

⋅ ⋅ 

l 

n 

∑ 

i= 

1 

p 

i 

⋅ μ 

α 

( y, 

e ) 

i 

34


V 

∑ 

i= 

1 


y 

= 

n 

p 

i 

Taglio nel traverso 

⋅ κ 

α 

2 ⋅ γP 

( y, 

ei 

) + 

γ + γ 

P 

E 

π 

⋅b 

⋅ ⋅ 

l 

n 

∑ 

i= 

1 

p 

i 

⋅ τ 

α 

( y, 

e 

i 

) 

35



36

IMPALCATO A GRATICCIO

Create successful ePaper yourself

Delete template?

Save as template?