Web Gnomonices! - Gnomonica by Nicola Severino

Traduzione di Riccardo Anselmi
Passaggio al meridiano e meridiano
di Denis Savoie
Sovente ci si impegna, quando si traccia un orologio solare, o a rilevare l’orientamento del muro, o a materializzare, sul
suolo, la linea Nord-Sud, altrimenti detta il meridiano locale.
In generale, si ricorre al sole, calcolando per mezzo delle effemeridi, l’istante del suo passaggio al meridiano del luogo;
in questo istante ci si serve o dell’ombra di un filo a piombo o di un gnomone verticale.
Ora è talvolta precisato che questo rilevamento deve essere eseguito al secondo, avendo avuto cura di regolare il proprio
orologio sull’ora del segnale orario: questa raccomandazione che potrebbe sembrare superflua, è però basata su una
particolarità del movimento del sole, la cui omissione può avere delle conseguenze spiacevoli sulla precisione futura del
quadrante solare.
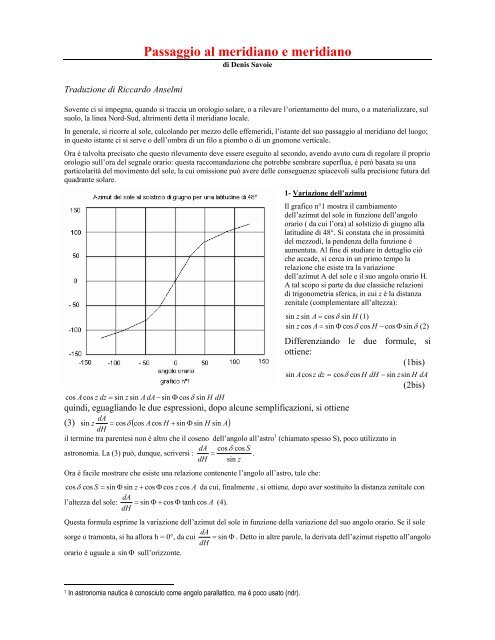
1- Variazione dell’azimut
Il grafico n°1 mostra il cambiamento
dell’azimut del sole in funzione dell’angolo
orario ( da cui l’ora) al solstizio di giugno alla
latitudine di 48°. Si constata che in prossimità
del mezzodì, la pendenza della funzione è
aumentata. Al fine di studiare in dettaglio ciò
che accade, si cerca in un primo tempo la
relazione che esiste tra la variazione
dell’azimut A del sole e il suo angolo orario H.
A tal scopo si parte da due classiche relazioni
di trigonometria sferica, in cui z è la distanza
zenitale (complementare all’altezza):
sin z sin A = cosδ
sin H (1)
sin z cos A = sin Φ cosδ
cos H − cos Φ sin δ (2)
Differenziando le due formule, si
ottiene:
(1bis)
sin A cos z dz = cosδ
cos H dH − sin zsin
H dA
(2bis)
cos A cos z dz = sin z sin A dA − sin Φ cosδ
sin H dH
quindi, eguagliando le due espressioni, dopo alcune semplificazioni, si ottiene
dA
(3) sin z = cosδ
( cos A cos H + sin Φ sin H sin A)
dH
il termine tra parentesi non è altro che il coseno dell’angolo all’astro 1 (chiamato spesso S), poco utilizzato in
dA cosδ cos S
astronomia. La (3) può, dunque, scriversi : = .
dH sin z
Ora è facile mostrare che esiste una relazione contenente l’angolo all’astro, tale che:
cosδ cos S = sin Φ sin z + cos Φ cos z cos A da cui, finalmente , si ottiene, dopo aver sostituito la distanza zenitale con
dA
l’altezza del sole: = sin Φ + cos Φ tanh cos A (4).
dH
Questa formula esprime la variazione dell’azimut del sole in funzione della variazione del suo angolo orario. Se il sole
dA
sorge o tramonta, si ha allora h = 0°, da cui = sin Φ . Detto in altre parole, la derivata dell’azimut rispetto all’angolo
dH
orario è uguale a sin Φ sull’orizzonte.
1 In astronomia nautica è conosciuto come angolo parallattico, ma è poco usato (ndr).