buigpunt 1
buigpunt 1
buigpunt 1
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
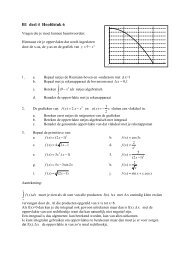
Buigpunt<br />
In de analyse is een <strong>buigpunt</strong> van een kromme een punt op de kromme waar de<br />
kromming van teken verandert. De vorm van de kromme verandert van hol (concaaf)<br />
in bol (convex) of omgekeerd.<br />
Karakterisering<br />
In een <strong>buigpunt</strong> stellen we de kromme lokaal voor door de functie f. Is de kromme de<br />
grafiek van een functie dan geven we die ook door f aan. In het <strong>buigpunt</strong> is f in ieder<br />
geval differentieerbaar. Afhankelijk van de verdere differentieerbaarheid van f in het<br />
<strong>buigpunt</strong>, laat zich een <strong>buigpunt</strong> als volgt karakteriseren:<br />
in het <strong>buigpunt</strong> kruist de raaklijn de kromme;<br />
in het <strong>buigpunt</strong> bereikt de afgeleide van f een extremum.<br />
Als ook de tweede afgeleide bestaat kan deze laatste voorwaarde ook geformuleerd<br />
worden als:<br />
in het <strong>buigpunt</strong> wisselt de tweede afgeleide van f van teken (het teken van de<br />
tweede afgeleide geeft immers de kromming aan).<br />
Een <strong>buigpunt</strong>en kan een stationair punt op de grafiek van een functie zijn, maar in<br />
een <strong>buigpunt</strong> is een functie nooit extreem.<br />
De bovenstaande karakteriseringen geven de weg aan waarlangs <strong>buigpunt</strong>en<br />
opgespoord kunnen worden.<br />
In het geval de functie voldoende vaak differentieerbaar is, is de eis dat het teken<br />
van de tweede afgeleide rond dit punt van teken wisselt, equivalent met de eis dat<br />
de eerste van 0 verschillende afgeleide van oneven orde moet zijn (derde, vijfde, ...).<br />
Indien de eerste van 0 verschillende afgeleide van even orde is (tweede, vierde, ...)<br />
dan is er geen <strong>buigpunt</strong>.
Voorbeelden<br />
f(x) = cos(x) (rood) f'(x)= - sin(x) (groen) en f"(x) = - cos(x) (blauw)<br />
Voorbeeld 1<br />
We zoeken de <strong>buigpunt</strong>en van de functie cos(x).<br />
Op de figuur (rechts) is de functie samen met zijn eerste en tweede afgeleide<br />
weergegeven.<br />
cos(x) in het rood, cos'(x) in het groen en cos"(x) in het blauw.<br />
We bepalen de eerste en de tweede afgeleide<br />
We zien dat de nulpunten van cos(x) overeenkomen met de nulpunten van de<br />
tweede afgeleide.<br />
De eerste afgeleide bereikt er telkens een extremum en heeft er ook een<br />
constant teken rond zodat we steeds een <strong>buigpunt</strong> hebben.<br />
De nulpunten van de cosinus zijn dus ook de <strong>buigpunt</strong>en (analoog bij de sinus,<br />
sinus hyperbolicus en cosinus hyperbolicus).<br />
f(x) = x 3 + 3x 2 - 3x - 1<br />
.
Voorbeeld 2<br />
We zoeken de <strong>buigpunt</strong>en van de functie<br />
De functie is in het blauw weergeven op de figuur (rechts)<br />
We bepalen de eerste en tweede afgeleide<br />
De tweede afgeleide wordt 0 voor x = -1.<br />
Het teken van de eerste afgeleide rond dit punt is constant, namelijk<br />
negatief, dus is het een <strong>buigpunt</strong> (rood op de figuur).<br />
f(x) = x 3 (blauw), f'(x) = 3x 2 (rood)<br />
Voorbeeld 3<br />
Tenslotte bekijken we een klassiek voorbeeld, de functie f(x) = x 3 .<br />
We bepalen opnieuw eerste en tweede afgeleide<br />
De functie is in het blauw weergegeven op de figuur (rechts), samen<br />
met de eerste afgeleide (in het rood).<br />
We zien dat de tweede afgeleide 0 wordt voor x = 0. Op de grafiek is<br />
duidelijk te zien dat het teken van de eerste afgeleide constant is rond<br />
dit punt, namelijk positief. Bijgevolg is er in de oorsprong een <strong>buigpunt</strong>.<br />
Merk op dat ook de eerste afgeleide in dat punt 0 is, het is dus een<br />
stationair punt. De functie bereikt er echter geen extremum.