TÉCNICAS HEURÍSTICAS PARA OPTIMIZAÇÃO COMBINATÓRIA

Técnicas Heurísticas para Optimização Combinatória Jorge P. J. Santos 

TÉCNICAS HEURÍSTICAS PARA 

OPTIMIZAÇÃO COMBINATÓRIA 

CARACTERIZAÇÃO DOS PROBLEMAS DE OPTIMIZAÇÃO 

COMBINATÓRIA 

Dados: 

F → um domínio enumerável de soluções admissíveis (permutações, 

conjuntos, inteiros, grafos) 

c → Função custo (medida de ineficiência) 

Problema 

c: F → IR n 

(extensão natural: avaliação com critérios múltiplos) 

Minimize c 

Sujeito a f∈F 

1 


PROBLEMAS DE OPTIMIZAÇÃO COMBINATÓRIA: 

MODELOS E APLICAÇÕES 

1 Árvore de Suporte de Custo Mínimo 

Definição do Problema 

Este problema consiste em determinar uma árvore de suporte (grafo com 

um e um só caminho entre qualquer par de nós) com custo mínimo numa 

rede da forma 

1 

5 

5 

2 

4 

Formulação Matemática do Problema 

4 

3 

5 

Sejam A o conjunto das árvores de suporte da rede e f(A) o custo da árvore 

A. O problema pode ser formulado da seguinte forma 

3 

4 

4 

3 

minimize z = f(A) 

sujeito a A∈A 

2 

2 

Custo do arco (i,j) 

6 

5 

1 

6 

3 

3 

7


2 Problema do Caminho Mais Curto 


Este problema consiste em determinar um caminho mais curto entre um nó 

inicial s e um nó terminal t num grafo da forma 

s 


Parâmetros 

N = {1,2,3,4,5,6} representa o conjunto de nós 

A = {(1,2),(1,3),(1,4),(2,3),(2,5),(2,6),(3,4),(3,5),(4,5),(5,6)} 

representa o conjunto de arcos 

cij ((i,j)∈A) representa o custo de atravessar o arco (i,j) 

Variáveis: 

1 

Função objectivo 

2 

1 

3 

3 

1 

1 

4 

2 

3 

3 

⎧1 

se caminho contém o arco ( i, 

j) 

xij = ⎨ 

⎩0 

caso contrário 

minimize z = 

( ) ∑ c ij xij 

i, 

j ∈A 

3 

5 

5 

4 

6 

3 t 

Custo de atravessar 

o arco (i,j) 


Restrições 

1. No caminho existe apenas um arco que sai do nó inicial s 

x12 + x13 + x14 = 1 ⇔ ∑ x sj − ∑ x js = 1 

j: 

( s, 

j) 

∈A j: 

( j, 

s) 

∈A 

2. No caminho existe apenas um arco que termina no nó final t 

x26 + x56 = 1 ⇔ ∑ x tj − ∑ x jt = −1 

j: 

( t, 

j) 

∈A j: 

( j, 

t) 

∈A 

3. O número de arcos que sai do nó i menos o número que entra no 

mesmo é igual a zero 

x 23 + x 25 + x 26 − x 12 = 0 

x 34 + x 35 − x 13 − x 23 = 0 

x 45 − x 14 − x 34 = 0 

x 56 − x 25 − x 35 − x 45 = 0 

Programa Binário 

minimize z = 


i, 

j ∈A 

sujeito a 

⇔ ∑ x ij − ∑ x ji = 0 (i≠s,t) 

j: 

( i, 

j) 

∈A j: 

( j, 

i) 

∈A 

⎧ 1 se i = s 

⎪ 

∑ xij 

− ∑ x ji = ⎨ 0 se i ≠ s, 

t 

j: 

( i, 

j) 

∈A j: 

( j, 

i) 

∈A 

⎪ 

⎩−1 

se i = t 

xij∈{0,1}, (i,j)∈A 

4


3 Problema do Fluxo Máximo 


Este problema consiste em determinar o fluxo máximo que pode ser 

enviado de um nó inicial s para um nó terminal t num grafo da forma 

2 

6 

5 

9 3 7 

3 

4 

t 

1 3 14 6 

7 

8 

s 

2 3 

4 

1 

3 

7 

3 

capacidade 

do arco (i,j) 


Parâmetros 

N = {1,2,3,4,5,6,7,8} representa o conjunto de nós 

A = {(1,2),(1,4),(2,3),(2,5),(3,6),(4,3),(4,7),(5,3),(5,8),(6,5),(6,7),(6,8),(7,8)} 


uij ((i,j)∈A) representa a capacidade do arco (i,j) 

Variáveis: 

xij ((i,j)∈A) representa a quantidade de fluxo que atravessa o arco (i,j) 

f representa o fluxo a enviar do nó s para o nó t 


maximize z = f 

5 


Restrições 

1. A quantidade de fluxo que sai do nó s é igual a f 

x12 + x14 = f ⇔ ∑ xsj 

− ∑ x js = f 

j: 

( s, 

j) 

∈ A j: 

( j, 

s) 

∈A 

2. A quantidade de fluxo que entra no nó t é igual a f 

x58 + x68 + x78 = f ⇔ ∑ xtj 

− ∑ x jt = − f 

j: 

( t, 

j) 

∈ A j: 

( j, 

t) 

∈A 

3. A quantidade de fluxo que sai do nó i menos a quantidade de fluxo 

que entra no mesmo nó é igual a zero 

x23 + x25 − x12 = 0 

x36 − x23 − x43 − x53 = 0 

x43 + x47 − x14 = 0 

x53 + x58 − x25 − x65 = 0 

x65 + x67 + x68 − x36 = 0 

x78 − x47 − x67 = 0 

⇔ ∑ x ij − ∑ x ji = 0 (i≠s,t) 

j: 

( i, 

j) 

∈A j: 

( j, 

i) 

∈A 

4. A quantidade de fluxo que atravessa o arco (i,j) não pode ultrapassar 

a sua capacidade nem ser negativo 

Programa Linear 

0 ≤ x ij ≤ u ij , (i,j)∈A 

maximize z = f 

sujeito a 

⎧ f 

⎪ 

∑ xij 

− ∑ x ji = ⎨ 0 

j: 

( i, 

j) 

∈A j: 

( j, 

i) 

∈A 

⎪ 

⎩− 

f 

se 

se 

se 

i = s 

i ≠ s, 

t 

i = t 

0 ≤ x ij ≤ u ij , (i,j)∈A 

6


4 Problema do Fluxo de Custo Mínimo 


Este problema consiste em determinar a forma como deve ser distribuído o 

fluxo num grafo de modo a que os requerimentos sejam satisfeitos 


Parâmetros 

N = {1,2,3,4,5,6,7,8} representa o conjunto de nós 

A = {(1,2),(1,4),(2,4),(2,5),(3,2),(3,5),(4,6),(4,7),(5,4),(5,7),(5,8),(7,6),(7,8)} 


cij ((i,j)∈A) representa o custo unitário de atravessar o arco (i,j) 

bi (i∈N) representa o requerimento do nó i 

Variáveis: 

[45] 

[45] 

3 

1 

[20] 2 

3 

3 

xij ((i,j)∈A) representa a quantidade de fluxo que atravessa o arco (i,j) 


8 

2 

1 

4 

[0] 

4 

3 

5 

[0] 

2 

minimize z = 


i, 

j ∈A 

7 

7 

5 

6 

6 

7 

8 

1 

4 

[−50] 

[−20] 

[−40] 

Requerimento 

do nó i 

Custo unitário de 

atravessar o arco (i,j) 


Restrições 

1. A quantidade de fluxo que sai do nó i menos a quantidade de fluxo 

que entra no mesmo nó é igual ao requerimento desse mesmo nó 

x 12 + x 14 = 45 

x 24 + x 25 − x 12 − x 32 = 20 

x 32 + x 35 = 45 

x 46 + x 47 − x 14 − x 24 − x 54 = 0 

x 54 + x 57 + x 58 − x 25 − x 35 = 0 

− x 46 − x 76 = −50 

x 76 + x 78 − x 47 − x 57 = −20 

− x 58 − x 78 = −40 

8 

⇔ ∑ x ij − ∑ x ji = bi 

j: 

( i, 

j) 

∈ A j: 

( j, 

i) 

∈A 

(i∈N) 

2. A quantidade de fluxo que atravessa o arco (i,j) não pode ser 

negativo 

Programa Linear 

minimize z = 


i, 

j ∈A 

x ij ≥ 0, (i,j)∈A 

sujeito a ∑ x ij − ∑ x ji = bi 

j: 

( i, 

j) 

∈ A j: 

( j, 

i) 

∈A 

x ij ≥ 0, (i,j)∈A 

(i∈N)


5 Problema de Localização Sem Capacidades 


Pretende-se fazer um estudo sobre a localização de aterros sanitários em 5 

locais possíveis que irão receber os resíduos domésticos e industriais de 7 

concelhos. Os custos anuais de funcionamento dos aterros sanitários e de 

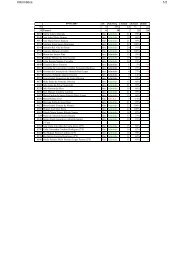
transporte entre os concelhos e os aterros são dados pela tabela seguinte: 

Concelhos 

Aterros 

1 2 3 4 5 6 7 

9 

Custos de 

Funcioanamento 

1 50 25 85 10 20 60 40 120 

2 90 20 10 95 80 70 95 100 

3 80 15 15 90 60 60 30 160 

4 10 90 20 95 90 50 60 130 

5 20 95 60 20 20 70 70 140 

Qual a localização ideal dos aterros sanitários e a respectiva afectação aos 

concelhos, de forma a que o custo total seja mínimo. 


Parâmetros 

m representa o número de locais possíveis para a instalação dos aterros 

sanitários (m = 5) 

n representa o número de concelhos (n = 7) 

cij (i=1,2,...,m; j=1,2,...,n) representa o custo anual de afectar o aterro sanitário 

i ao concelho j, 

fi (i=1,2,...,m) representa o custo anual de funcionamento de um aterro 

sanitário em i. 


Variáveis: 

⎧1 

se o aterro sanitário i é afectado ao concelho j 

xij = ⎨ 

⎩0 


⎧1 

se for instalado um aterro sanitário no local i 

yi = ⎨ 

⎩0 



Restrições 

m n m 

minimize z = ∑∑cij 

xij 

+ ∑ fi 

yi 

i= 

1j= 1 i= 

1 

1. Cada concelho é servido por um e um só aterro 

x11 + x21 + x31 + x41 + x51 = 1 

x 12 + x 22 + x 32 + x 42 + x 52 = 1 

x 13 + x 23 + x 33 + x 43 + x 53 = 1 

x 14 + x 24 + x 34 + x 44 + x 54 = 1 

x 15 + x 25 + x 35 + x 45 + x 55 = 1 

x 16 + x 26 + x 36 + x 46 + x 56 = 1 

x 17 + x 27 + x 37 + x 47 + x 57 = 1 

10 

m 

⇔ ∑ x ij = 1, 

j=1,2,...,n 

i= 

1


2. Obrigação de instalação de um aterro sanitário num local, sempre 

que a ele seja afectado a um concelho 

x 11 ≤ y 1 , x 21 ≤ y 2 , x 31 ≤ y 3 , x 41 ≤ y 4 , x 51 ≤ y 5 , 

x 12 ≤ y 1 , x 22 ≤ y 2 , x 32 ≤ y 3 , x 42 ≤ y 4 , x 52 ≤ y 5 , 

x 13 ≤ y 1 , x 23 ≤ y 2 , x 33 ≤ y 3 , x 43 ≤ y 4 , x 53 ≤ y 5 , 

x 14 ≤ y 1 , x 24 ≤ y 2 , x 34 ≤ y 3 , x 44 ≤ y 4 , x 54 ≤ y 5 , 

x 15 ≤ y 1 , x 25 ≤ y 2 , x 35 ≤ y 3 , x 45 ≤ y 4 , x 55 ≤ y 5 , 

x 16 ≤ y 1 , x 26 ≤ y 2 , x 36 ≤ y 3 , x 46 ≤ y 4 , x 56 ≤ y 5 , 

x 17 ≤ y 1 , x 27 ≤ y 2 , x 37 ≤ y 3 , x 47 ≤ y 4 , x 57 ≤ y 5 . 

Ou seja 


xij − yi ≤ 0, i=1,2,...,m; j=1,2,...,n 

m n m 

Minimize z = ∑∑cij 

xij 

+ ∑ fi 

yi 

i= 

1j= 1 i= 

1 

m 

sujeito a ∑ x ij = 1, 

j=1,2,...,n 

i= 

1 

xij − yi ≤ 0, i=1,2,...,m; j=1,2,...,n 

xij ∈ {0,1}, i=1,2,...,m; j=1,2,...,n 

yi ∈{0,1}, i=1,2,...,m 

11 


6 Problema de Localização Com Capacidades 


Uma empresa pretende fazer um estudo sobre a localização das fábricas a 

construir em 5 locais possíveis que irão abastecer 6 armazéns. Os custos 

fixos de funcionamento diários das fábricas e os custos unitários de 

transporte entre as fábricas e os armazéns são dados pela tabela seguinte: 

Armazéns 

Fábricas 

1 2 3 4 5 6 Capacidade 

Produtiva 

12 

Custos de 

Funcion. 

1 4 2 5 1 2 6 1000 2500 

2 7 2 2 9 8 7 1400 2000 

3 8 1 1 3 3 6 2000 3300 

4 1 9 2 9 9 5 1900 2800 

5 2 4 6 2 1 7 1500 2900 

Procura diária 500 800 400 900 700 600 

Formule o problema. 


Parâmetros 

m representa o número de localizações possíveis das fábricas (m = 5) 

n representa o número armazéns (n = 6) 

ai (i=1,2,...,m) representa a capacidade produtiva da fábrica i. 

bj (j=1,2,...,n) representa a procura diária do armazém j. 

cij (i=1,2,...,m; j=1,2,...,n) representa o custo unitário de transporte 

entre a fábrica i e o armazém j, 

fi (j=1,2,...,m) representa custo fixo de funcionamento diário de uma 

fábrica no local i.


Variáveis: 

xij (i=1,2,...,m; j=1,2,...,n) representa a quantidade que deve ser enviada 

da fábrica localizada em i para o armazém j 

⎧1 

se for instalado uma fábrica no local i 

yi = ⎨ 

(i=1,2,...,m) 

⎩0 



Restrições 

m n m 

minimize z = ∑∑cij 

xij 

+ ∑ fi 

yi 

i= 

1j= 1 i= 

1 

1. Procura diária dos armazéns 

x11 + x21 + x31 + x41 + x51 = 500 

x 12 + x 22 + x 32 + x 42 + x 52 = 800 

x 13 + x 23 + x 33 + x 43 + x 53 = 400 

x 14 + x 24 + x 34 + x 44 + x 54 = 900 

x 15 + x 25 + x 35 + x 45 + x 55 = 700 

x 16 + x 26 + x 36 + x 46 + x 56 = 600 

13 

m 

⇔ ∑ x ij = b j , j=1,2,...,n 

i=1 


2. Capacidades das fábricas 

x 11 + x 12 + x 13 + x 14 + x 15 + x 16 ≤ 1000y 1 

x 21 + x 22 + x 23 + x 24 + x 25 + x 26 ≤ 1400y 2 

x 31 + x 32 + x 33 + x 34 + x 35 + x 36 ≤ 2000y 3 

x 41 + x 42 + x 43 + x 44 + x 45 + x 46 ≤ 1900y 4 

x 51 + x 52 + x 53 + x 54 + x 55 + x 56 ≤ 1500y 5 

3. Não faz sentido transportar quantidades negativas 

Programa Binário Misto 

xij ≥ 0, i=1,2,...,m; j=1,2,...,n 

m n m 

Minimize z = ∑∑cij 

xij 

+ ∑ fi 

yi 

i= 

1j= 1 i= 

1 

m 

sujeito a ∑ x ij = b j , j=1,2,...,n 

i=1 

n 

∑ x ij − ai 

yi 

≤ 0, 

i=1,2,...,m 

j = 1 

14 

n 

⇔ ∑ x ij − ai 

yi 

≤ 0, 

i=1,2,...,m 

j = 1 

xij ≥ 0, i=1,2,...,m; j=1,2,...,n 

yi ∈{0,1}, i=1,2,...,m


7 Problema da Cobertura de Conjuntos 


Uma empresa de telecomunicações móveis pretende instalar novas antenas 

em 6 locais possíveis para fazer a cobertura de 5 zonas geográficas. As 

zonas que cada antena cobre, assim como os custos de instalação são 

dados pela tabela seguinte 

Antenas 1 2 3 4 5 6 

Zonas geográficas cobertas 1,2,3 4,5 1,4 2,5 1,3 2,3,5 

Custo de Instalação 900 800 400 300 500 900 

Formule o problema. 


Parâmetros 

m representa as zonas geográficas a cobrir pelas antenas (m = 5) 

n representa o número de locais possíveis para instalar antenas (n = 6) 

cj (j=1,2,...,n) representa o custo de instalação da antena no local j. 

⎧1 

se a antena instalada no local j pode servir a zona geográfica i 

aij = ⎨ 

⎩0 


(i=1,2,...,m; j=1,2,...,n) 

Variáveis: 

⎧1 

se for instalada uma antena no local j 

x j = ⎨ 

(j=1,2,...,n) 

⎩0 


15 



Restrições 

n 

minimize z = ∑ c j x j 

j = 1 

Cobertura do conjunto das zonas geográficas pelas antenas 

x1 + x3 + x5 ≥ 1 

x 1 + x 4 + x 6 ≥ 1 

x 1 + x 5 + x 6 ≥ 1 

x 2 + x 3 ≥ 1 


x 2 + x 4 + x 6 ≥ 1 

n 

Minimize z = ∑ j j 

j = 

x c 

1 

n 

⇔ ∑ a ij x j ≥ 1, 

i=1,2,...,m 

j = 1 

n 

sujeito a ∑ a ij x j ≥ 1, 

i=1,2,...,m 

j = 1 

xj ∈{0,1}, j=1,2,...,n 

16


8 Problema da Partição de Conjuntos 


Parâmetros 

m representa entidades (objectos) a servir 

n representa o número de locais possíveis 

cj (j=1,2,...,n) representa o custo de instalação no local j. 

⎧1 

se o local j pode servir o objecto i 

aij = ⎨ 

(i=1,2,...,m; j=1,2,...,n) 

⎩0 


Variáveis: 

⎧1 

se o local j for escolhido 

x j = ⎨ 

(j=1,2,...,n) 

⎩0 



n 

Minimize z = ∑ c j x j 

j = 1 

n 

sujeito a ∑ a ij x j = 1, 

i=1,2,...,m 

j = 1 

xj ∈{0,1}, j=1,2,...,n 

17 


9 Problema do Empacotamento de Conjuntos 


Parâmetros 

m representa entidades (objectos) a servir 

n representa o número de locais possíveis 

cj (j=1,2,...,n) representa o custo de instalação no local j. 

⎧1 

se o local j pode servir o objecto i 

aij = ⎨ 

(i=1,2,...,m; j=1,2,...,n) 

⎩0 


Variáveis: 

⎧1 

se o local j for escolhido 

x j = ⎨ 

(j=1,2,...,n) 

⎩0 



n 

Maximize z = ∑ c j x j 

j = 1 

n 

sujeito a ∑ a ij x j ≤ 1, 

i=1,2,...,m 

j = 1 

xj ∈{0,1}, j=1,2,...,n 

18


BREVE INTRODUÇÃO À COMPLEXIDADE COMPUTACIONAL 

Problema P 

Tamanho de uma instância n Algoritmo A 

(codificada em binário) 

TEMPO 

Nº de operações elementares 

(somas, comparações, …) 

“Worst Case” 10n 3 + 5n 2 

(pior dos casos) 

“rate of growth” O(n 3 ) 

(taxa de crescimento) 

[bons] Algoritmos Polinomiais Algoritmos exponenciais [Maus] 

O(n 3 ) O(n ln n) O(2 n ) 

Classificação dos algoritmos 

- “recognition problems” 

- as classes P e N P 

- problemas NP-completos 

- problemas FÁCEIS e DIFÍCEIS 

19 


Crescimento de funções polinomiais e exponenciais 

Função Valores aproximados 

n 10 100 1 000 

n ln n 33 664 9 966 

n 3 1 000 1 000 000 10 9 

10 6 n 8 10 14 10 22 10 30 

2 n 1 024 1.27×10 30 1.05×10 301 

n log n 2 099 1.93×10 13 7.89×10 29 

n! 3 628 800 10 158 4×10 2567 

Os algoritmos polinomiais aproveitam melhor a tecnologia 

Função 

Tamanho do problema 

resolvido num dia 

20 

Idem num computador dez 

vezes mais rápido 

n 10 12 10 13 

n ln n 0.948×10 11 0.87×10 12 

n 2 10 6 3.16×10 6 

n 3 10 4 2.15×10 4 

10 8 n 4 10 18 

2 n 40 43 

10 n 12 13 

n log n 79 95 

n! 14 15 

Fonte: Papadimitriou and Steiglitz, 1982


Análise do “Worst Case” 

→ garantia absoluta 

→ independente do COMPUTADOR 

da IMPLEMENTAÇÃO 

das “INSTÂNCIAS” PARTICULARES 

→ medida muito conservadora (PESSIMISTA) 

→ retrata “mal” a PERFORMANCE EFECTIVA de um 

algoritmo 

Análise Probabilística 

→ assume hipóteses sobre a distribuição probabilística dos 

INPUTS 

e deriva resultados analíticos sobre a distribuição dos 

OUPUTS 

→ geração de “instâncias” aleatórias (SIMULAÇÃO) 

PROGRAMAÇÃO LINEAR - LP 

SIMPLEX Dantzig 1947 

ELIPSOÍDE Khachian 1979 

MÉTODOS PROJECTIVOS Karmarkar 1984 

21 


Alguns problemas fáceis 

→ Transportes 

→ Afectação 

→ Árvore Geradora de Custo Mínimo 

→ Caminho Mais Curto 

→ Fluxo Máximo 

→ Fluxo de Custo Mínimo 

→ Programação Linear 

Alguns problemas difíceis 

→ Mochila 0-1 

→ Mochila Inteiro 

→ Caixeiro Viajante 

→ Localização Sem/Com capacidades 

→ Cobertura de Conjuntos 

→ Partição de Conjuntos 

→ Empacotamento de Conjuntos 

→ Programação Inteira Binária 

→ Programação Inteira 

→ Programação Inteira Mista 

22


Como abordar então os problemas combinatórios “intratáveis”? 

⇒ HEURÍSTICAS 

Ideia: Usar a estrutura do problema para obter SOLUÇÕES 

SATISFATÓRIAS de uma forma eficiente 

EFICIÊNCIA E EFICÁCIA DOS ALGORITMOS 

Eficiência 

(rapidez) 

a 

“ depressa e bem há pouco quem” 

23 

b 

Eficácia 

(qualidade da solução) 


ESTRUTURA TÍPICA DE UMA ABORDAGEM HEURÍSTICA 

1 

2 

CUSTO 

$ 

Construção de uma algoritmos “GREEDY” 

SOLUÇÃO INICIAL “dispatching rules” 

24 

(prioridades) 

Melhoramentos procedimentos 

Iterativos de 

Até se atingir um 

“óptimo local” 

“TROCAS” 

Soluções


ALGORITMOS DE PESQUISA LOCAL 

Heurísticas de melhoramentos (Pesquisa local − “local Search”) 

Vizinhanças (Neighbouroods) 

Dado um problema com instâncias (F,c), uma vizinhança N é uma função 

N: F → 2 F 

A escolha de N é critica: estrutura das soluções 

Exemplo: Problema do Caixeiro Viajante 

Solução vizinha: 2-change (troca de dois vértices) 

1 

2 5 

Em geral: k-change 

3 4 6 

7 

25 

1 

f 

N(f) 

F 

2 5 

3 4 6 

7 


Sub-Vizinhanças 

A “análise” é feita apenas sobre um subconjunto [de cardinalidade 

“parametrizável”] de soluções escolhidas aleatoriamente na vizinhança 

Restrição natural e 

“prática” das estratégias 

de pesquisa local 

Estratégias de pesquisa 

− procuarar a melhor solução na vizinhança N(x) (ou na subvizinhança 

SN(x)) 

− procurar, até encontrar uma solução melhor que x 

Constituem a base de um PROCESSO ITERATIVO cuja regra de 

paragem é, em geral, simples (n iterações) 

Esforço computacional 

− processo de identificação (enumeração) das soluções vizinhas 

− “avaliação” dessas soluções (pode ser um esforço grande) 

26 

x 

N(x) 

SN(x) 

F


PROBLEMA DA MOCHILA 0-1 

Problema 

Artigo j 1 2 3 4 5 6 

Valor unitário cj 12 14 15 24 24 17 

Peso unitário aj 15 14 14 18 17 12 

Maximizar o valor 

não ultrapassando o peso máximo (60) 

Variáveis de decisão 

⎧1 

se o artigo j é escolhido 

x j = ⎨ 

⎩0 


Formulação Matemática do problema 

max 12x1 + 14x2 + 15x3 + 24x4 + 24x5 + 17x6 s.a. 15x1 + 14x2 + 14x3 + 18x4 + 17x5 + 12x6 ≤ 60 

x j ∈{0,1} 

27 


Uma heurística construtiva 

valor 

Ordenar os artigos por rácio e ir metendo na mochila os artigos por 

peso 

essa ordem 

valor 

peso 

1 2 3 4 5 6 

12 

15 

14 

14 

15 

14 

28 

24 

18 

24 

17 

17 

12 

0.80 1.00 1.07 1.33 1.41 1.42 

Uma heurística de melhoramentos 

× × × 3º 2º 1º 

Σ = 47 Σ = 29 Σ = 12 

Trocar artigos que estão dentro da mochila com artigos que estão fora 

4 

5 

6 

2 

1 

3


PROBLEMA DO CAIXEIRO VIAJANTE 

Heurísticas de construção de percursos 

Menor custo de inserção 

Passo 0: Escolha um subpercurso inicial com duas cidades i1 e i2 tais 

que: 

29 

( d d ) 

d i i + di 

i = mínimo ij + 

i V , j V 

i≠ 

j 

∈ ∈ 

1 2 2 1 

com V = {1,2,…,n} o conjunto de cidades. 

Passo 1: Determine o vértice k não pertencente ao subpercurso com 

menor valor 

dik + dkj 

− dij 

= mínimo d pk + dkq 

− d 

( p, 

q) 

∈T 

com T o percurso já construído. 

ji 

( ) 

Passo 2: Insera o nó k entre os nós i e j. Se não houver mais nós para 

inserir, pare com o subpercurso obtido. Caso contrário, volte 

ao passo 1. 

Vizinho mais próximo 

Passo 0: Sejam i uma cidade inicial e V = {1,2,…,n}−{i} o conjunto 

de cidades a visitar. 

Passo 1: Calcule a cidade j mais próxima da cidade i a partir de: 

dij 

= mínimo dip 

p∈V 

Passo 2: Insira a cidade j imediatamente a seguir a i e faça 

i = j e V = V − {j} 

Passo 3: Se V = ∅, termine. Caso contrário, volte ao passo 1. 

pq 

(*) 


Heurísticas de melhoramento de percursos 

As heurísticas de melhoramentos de percursos consistem em, a partir de 

um percurso inicial, efectuar permutações de k arcos. Ou seja, em 

substituir k arcos do percurso por k arcos não pertencentes ao percurso. 

Estas substituições terão de manter um percurso pelas n cidades e só se 

realizam se houver uma redução do valor da função objectivo. O caso 

k = 2 é descrito através do seguinte algoritmo 

Passo 0: Considere um percurso inicial 

Passo 1: Avalie o valor (redução ou aumento) de todas as trocas de 

dois arcos não consecutivos para o percurso corrente: 

i 

k 

l 

j 

Passo 2: Se nenhuma das potenciais trocas de dois arcos conduziu a 

uma redução, termine com o percurso corrente. Caso 

contrário actualize o percurso com a troca a que maior 

redução conduziu e volte ao passo 1. 

Nota: Os resultados computacionais até agora relatados na literatura 

apontam para o valor k = 3 como o mais adequado. Quatro trocas de 

arcos falha por ineficiência no processo de troca de arcos enquanto que 

duas trocas conduz a soluções não tão boas como desejáveis. 

30 

i 

k 

l 

j


META-HEURÍSTICAS PARA 

PROBLEMAS DE OPTIMIZAÇÃO COMBINATÓRIA 

Dificuldades com os métodos tradicionais 

- sofisticação (matemática) 

- custos/benefícios 

- esforço computacional 

- flexibilidade/robustez 

Estratégias de pesquisa local (local search) 

- estrutura de VIZINHANÇA (neighbourhood) ⇐ crítica 

- trajectória 

- estratégia de STEEP DESCENT ⇒ MÍNIMOS LOCAIS 

IDEIA: 

Permitir uma DEGRADAÇÃO TEMPORÁRIA 

da função objectivo 

31 


SIMULATED ANNEALING (AREFECIMENTO SIMULADO) 

• Considere uma solução actual x n 

• Escolher “à sorte” uma solução x em V(x n ) 

• Se x é melhor, x n ← x 

Se não: com probabilidade p(n) x n ← x 

(1−p(n)) mantém x n 

[p(n) decresce com o tempo − “temperatura” arrefece] 

Parâmetros 

a) escolha da probabilidade de aceitação 

⎛ 1 ⎞ 

p( n) 

= exp⎜− 

∆Fn 

⎟ 

⎝ T ( n) 

⎠ 

com ∆Fn = F(x) − F(xn ) 

b) escolha de um “TEMPERATURE SCHEDULE” 

T(n) 

T 0 

T 1 

T 2 

T 3 

L 

2L 

c) Escolha de uma REGRA DE PARAGEM 

3L 

4L 

32 

n 

T(kL) = T k = α k T 0 

Cooling rate 

(0


TABU SEARCH 

• Considere uma solução actual x n 

• Ir para a melhor solução admissível 

(mesmo que seja pior) 

da vizinhança V(x n ) ou sub-vizinhança V’(x n )⊆V(x n ) 

• Para evitar “CICLOS”, criar e manter uma 

LISTA TABU 

De pares (x n , x) dos movimentos recentes 

Parâmetros 

Dificuldades de gestão da informação 

Guardar atributos em vez de soluções na lista tabu 

[Exemplo: Caixeiro Viajante − troca de duas arestas] 

a) Estrutura de VIZINHANÇA ( e SUB-VIZINHANÇA) 

b) que atributos? 

c) Tamanho da LISTA TABU 

d) REGRA DE PARAGEM (fixar n iterações) 

33 


ALGORITMOS GENÉTICOS 

• Tratam POPULAÇÕES de soluções [paralelismo intrínseco] 

• Uma solução é CODIFICADA como uma sequência de tamanho 

finito num alfabeto finito − CROMOSSOMAS 

sobre a POPULAÇÃO da GERAÇÃO n 

é feita uma SELECÇÃO dos melhores indivíduos 

que são sujeitos a um processo de CRUZAMENTO 

(em pares) 

e com uma pequena probabilidade sofre uma 

MUTAÇÃO (alteração de um valor de um gene) 

dando origem à GERAÇÃO n+1 

A selecção é feita com maior probabilidade 

sobre os indivíduos mais ADAPTADOS 

[maior valor de FITNESS] 

transformação de 

função objectivo 

34


Operador de cruzamento [crossover] 

Pontos de crossover (aleatórios) 

0 1 0 1 1 0 0 1 0 1 0 0 0 0 0 1 

1 1 0 0 0 1 1 0 1 1 0 1 1 1 1 0 

Pais Filhos 

Operador de mutação [mutation] 

0 1 0 1 1 0 0 1 0 1 0 1 1 1 0 1 

Dificuldades 

Ponto de mutação 

(arbitrário) 

• criticidade do sistema de CODIFICAÇÃO (esquemas, codificação 

binária) 

• Convergência prematura (MIGRAÇÃO) 

• compromisso GENERALIDADE / EFICIÊNCIA 

35 


Exemplo: Problema do Caixeiro Viajante 

• Representar uma solução (ROTA) por uma lista ordenada das 

cidades: 

3 5 7 1 2 4 8 6 9 

• Operador CRUZAMENTO 

(o operador usual não funciona) 

A: 3 5 7 1 2 4 8 6 9 3 5 2 3 4 6 8 6 9 

B: 1 9 2 3 4 6 8 7 5 1 9 7 1 2 4 8 7 5 

sem sentido! 

Operador “especial” para permutações 

B: H 9 H 3 H 6 8 H 5 

B: 3 6 H H H H 8 5 9 

B’: 3 6 7 1 2 4 8 5 9 

3 

36 

5 

7 

1 

9 6 8 

4 

2

TÉCNICAS HEURÍSTICAS PARA OPTIMIZAÇÃO COMBINATÓRIA

Create successful ePaper yourself

Delete template?

Save as template?