In cazul rezolvǎrii prin modelare numericǎ apar câteva deosebiri ...

.................................. LUCRAREA Nr.3 Data ................
Anul II ETc seria A G…. g… N…
MODELAREA UNUI CÂMP ELECTROSTATIC PRODUS DE SARCINI DISTRIBUITE.
REZOLVARE ANALITICĂ ŞI NUMERICĂ (QFIELD)
1.INTRODUCERE
Orice problemă reală necesită pentru rezolvare o modelare, prin care se reţin aspectele esenţiale
ale problemei , echivalându-se unele aspecte complicate prin altele mai simple şi renuntându-se la aspecte
cu influenţă minoră în stabilirea soluţiei. Cu cât un model este mai simplu, cu atât şi rezolvarea problemei
este mai simpla şi mai rapidă (chiar prin prisma timpului de calcul pe ordinator). Pentru a avea o situaţie
mai apropiată de realitate modelul nu poate fi excesiv de simplu. Evident că şi în acest caz, ca şi în
majoritatea problemelor de tip ingineresc, trebuie găsit un echilibru între cele două tendinţe.
In cazul rezolvǎrii prin modelare numericǎ apar câteva deosebiri esenţiale faţǎ de situaţia realǎ:
- materia şi câmpul sunt caracterizate din punct de vedere macroscopic de noţiunea de continuu, iar
modelele numerice sunt caracterizate de noţiunea de discret
- asupra realitǎţii se poate face un calcul integro-diferenţial, pe când asupra modelelor numerice se
acţioneazǎ cu metode numerice, în principal iterative, de rezolvare.
In cadrul laboratorului vom utiliza şi modele fizice, care la o anumitǎ scarǎ , cu o anumitǎ precizie
şi cu anumite simplificǎri reproduc realitatea pe care vrem să o studiem. Asupra acestor modele se pot
face masurǎri directe şi prin relaţii de analogie şi corespondenţǎ, din aceste masurǎri se pot obţine
marimile ce ne intereseazǎ.
2. PROBLEMA PROPUSA PENTRU REZOLVARE PRIN MODELARE
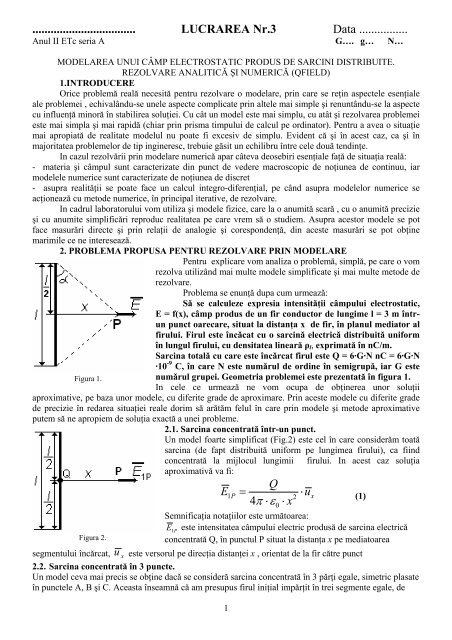
Pentru explicare vom analiza o problemǎ, simplă, pe care o vom
rezolva utilizând mai multe modele simplificate şi mai multe metode de
rezolvare.
Problema se enunţǎ dupa cum urmeazǎ:
Sǎ se calculeze expresia intensitǎţii câmpului electrostatic,
E = f(x), câmp produs de un fir conductor de lungime l = 3 m întrun
punct oarecare, situat la distanţa x de fir, în planul mediator al
firului. Firul este încǎcat cu o sarcinǎ electricǎ distribuitǎ uniform
în lungul firului, cu densitatea lineară ρl, exprimată în nC/m.
Sarcina totalǎ cu care este încǎrcat firul este Q = 6·G·N nC = 6·G·N
·10 -9 C, în care N este numǎrul de ordine în semigrupǎ, iar G este
Figura 1.
numǎrul grupei. Geometria problemei este prezentată în figura 1.
In cele ce urmeazǎ ne vom ocupa de obţinerea unor soluţii
aproximative, pe baza unor modele, cu diferite grade de aproximare. Prin aceste modele cu diferite grade
de precizie în redarea situaţiei reale dorim să arătăm felul în care prin modele şi metode aproximative
putem să ne apropiem de soluţia exactă a unei probleme.
2.1. Sarcina concentrată într-un punct.
Un model foarte simplificat (Fig.2) este cel în care considerǎm toatǎ
sarcina (de fapt distribuită uniform pe lungimea firului), ca fiind
concentratǎ la mijlocul lungimii firului. In acest caz soluţia
aproximativǎ va fi:
E
1P
1
x ⋅
Q
=
2
4π ⋅ε
⋅
Semnificaţia notaţiilor este următoarea:
0
E1 P este intensitatea câmpului electric produsă de sarcina electrică
concentrată Q, în punctul P situat la distanţa x pe mediatoarea
segmentului încărcat, x u Figura 2.
este versorul pe direcţia distanţei x , orientat de la fir către punct
2.2. Sarcina concentrată în 3 puncte.
Un model ceva mai precis se obţine dacǎ se consideră sarcina concentrată în 3 pǎrţi egale, simetric plasate
în punctele A, B şi C. Aceasta înseamnǎ cǎ am presupus firul iniţial impǎrţit în trei segmente egale, de
ux
(1)

lungime l/3, şi sarcina electricǎ Q/3 uniform distribuitǎ pe fiecare din acestea. Fiecare sarcină Q/3 o
consideram concentratǎ în centrul fiecǎruia din segmentele respective (în punctele A,B şi C).
Pentru acest caz se vor însuma vectorial cele trei
componente, fiecare componentǎ fiind datǎ de câte o sacinǎ
Q/3. Rezultatul compunerii vectorilor este cuprins în planul
ortogonal pe mijlocul firului (plan mediator), datoritǎ
condiţiilor de simetrie a configuraţiei. Cele două componente
determinate de sarcinile plasate în A şi B au aceeaşi valoare
Q / 3
E A = = E şi formează acelaşi unghi cu direcţia x,
2 C
4π
ε 0 d
astfel că suma lor vectorială va fi orientata doar după direcţia x.
Figura 3.
Distanţele AP şi CP sunt egale: d = [x 2 +(l / 3) 2 ] 1/2
Q / 3
EB = este orientat de asemenea după direcţia lui x, astfel că şi suma (rezultanta) vectorială
2
4π
ε x
0
E = E + E + E
3 P A B C este şi ea orientată după direcţia lui x.
⎛ Q / 3 x Q / 3 ⎞
⎛ 2x
1 ⎞
E ⋅u
= Q ⋅ ⋅ + ⋅
⎝ d d x ⎠
⎝ d x ⎠
9
9
9
3P
= ⎜2
⋅9
⋅10
⋅ + 9 ⋅10
⎟ x 3 10 ⎜ ⎟ u
2
2
3 2 x (2)
Se poate uşor înţelege cǎ prin continuarea operaţiunii de împǎrţire în segmente şi mai mici (spre
E 9 ca sumă a acţiunii a nouă sarcini
exemplu ficare treime se imparte din nou în trei, obţinându-se P
punctiforme Q/9) se va obţine un rezultat ceva mai precis, mai apropiat de o distribuţie liniară uniformă.
Se poate apoi continua tot asa şi se va ajunge la un model care se apropie tot mai mult de situaţia
realǎ (distribuţie continuǎ a sarcinii), prin adunarea a 27 de contribuţii (mai precis), apoi a 81de mici
segmente (şi mai precis), apoi 243 (încă şi mai precis) ş.a.m.d.
Cu cât numǎrul subdiviziunilor este mai mare, cu atât se complicǎ şi calculul. Utilizând metode
numerice de calcul se pot folosi şi modele mai complicate, cu un numǎr foarte mare de subdomenii.
Diferenţa între modelul discontinuu (discret) şi situaţia realǎ (continuu) poate fi sugeratǎ şi prin
compararea unei imagini reale cu un mozaic care prin foarte multe bucǎţele mici (discrete) încearcǎ sǎ
redea o imagine cât mai apropiată de cea realǎ (continuǎ).
2.3. Sarcina distribuită. Calcul analitic, conductor filiform de lungime l .
Se poate face un calcul analitic, folosind metode integro
diferenţiale de calcul şi, în acest caz, se poate lua în calcul faptul
că sarcina este distribuită uniform, cu densitatea liniară ρl = Q/l
,pe un fir conductor ideal extrem de subţire, filiform, adică fără
dimensiune radială, dar de lungime finită l. Calculăm câmpul în
planul mediator (perpendicular pe mijlocul segmentului)
Se poate observa, în figura 4, că pentru orice element
infinitezimal dy plasat în partea superioară există un element
simetric plasat în partea inferioară. Fiecare din aceste elemente îşi
aduce contribuţia (dE1 şi, respectiv, dE2) la câmpul total. Cele
două componente infinitezimale însumate vor da o rezultantă
(dEiP), în planul ortogonal, orientată perpendicular pe fir.
Q
⋅ dy
l ⋅sin
dEiP = 2
l
ρ β
⋅ cosα
⋅u
x = ⋅dy⋅
u
2
2 x (3)
4π
⋅ε
0 ⋅ r
2π
⋅ε
0 ⋅ r
Figura 4.
Prin integrarea acestei rezultante, dE, pentru a obţine
contribuţia întregului fir unghiul β baleiază valorile de la β = 90° la β = θ. θ este unghiul sub care se vede
punctul P de la unul din capetele firului, iar r este distanţa de la elementul infinitezimal dy la punctul P.
2

θ
2
x
x
ρl
sin β ⎛ x ⎞
r = ; y=
x ⋅ctgβ
; dy = − dβ
; EiP
= ∫ sin β ⋅ ⋅⎜
− dβ
⎟
2
2
2
sin β
sin β
2πε
x ⎝ β
π / 2 0
sin ⎠
Q ⋅ cosθ
ρl
⋅ cosθ
EiP =
⋅u
x = ⋅u
x (4)
2π
⋅l
⋅ε
0 ⋅ x 2π
⋅ε
0 ⋅ x
Dacă se poate considera că firul este foarte lung (teoretic infinit), mult mai lung decât distanţa la
care dorim calcularea câmpului (l>>x), putem face un calcul mai simplu, utilizând teorema lui Gauss.
Particularizarea rezultatului precedent obţinut pentru conductor de lungime finită se poate particulariza
pentru cazul unui conductor foarte lung (teoretic infinit) punând θ = 0.
Q
ρl
E∞P =
⋅u
x = ⋅u
x (5)
2π ⋅l
⋅ε
0 ⋅ x 2π
⋅ε
0 ⋅ x
De asemenea, se poate face un calcul analitic al componentelor şi rezultantei câmpului, produs de
un segment încărcat cu sarcina electrică uniform distribuită, într-un punct oarecare plasat coplanar cu
segmentul de fir încărcat.
2.4. Sarcina uniform distribuită pe un conductor filiform, presupus infinit lung; calcul utilizând
legea fluxului electric (teorema lui Gauss).
Legea fluxului electric, aplicată pe suprafaţa închisă
cilindrică Σ, alcătuită din cele două baze Sb1 şi Sb2, precum şi din
suprafaţa laterală Slat se scrie :
D ⋅ dS
= Q
(6)
3
∫ Σ
∫ D ⋅ dS
= ∫D⋅dS+
Σ
= 0 + 0 +
Σ
D ⋅ dS
+
Sb 2
Slat
∫ D ⋅ dS ⋅ 0 ∫
Slat
Sb1 ∫
= ε E(
r)
dS = ε E(
r)
⋅ 2π
⋅ r ⋅h
Slat
∫
1 0
D ⋅dS
=
În integrala pe suprafaţa laterală, Slat , E(r) s-a putut scoate
în afara semnului de integrală pentru că, din condiţii de simetrie,
Elat (ca modul) are o acceaşi valoare, E(r), în orice punct al
suprafeţei laterale cilindrice ( r fiind acelaşi).
Atât pe baza superioară, b1, cât şi pe cea inferioară, b2, D = ε 0 E şi
dS sunt vectori perpendiculari, deci integralele respective sunt
nule (cos90 ° = 0). Pe suprafaţa laterală a lui Σ, D = ε 0 E şi dS sunt vectori omoparaleli (cos 0 ° Figura 5.
=1), iar pe
Slat modulul lui D (deci şi al lui E) este constant, fiecare punct de pe suprafaţa laterală fiind în condiţii
identice faţa de orice alt punct situat pe aceeaşi suprafaţă, la aceeaşi distanţă r faţă de axa de simetrie a
figurii (axă care coincide de fapt cu conductorul filiform).
QΣ este sarcina repartizată pe fir şi este acea parte a
sarcinii care se găseşte în interiorul suprafeţei închise Σ. Este
vorba de o porţiune de lungime h, încărcata cu o sarcină
Figura 6.
uniform distribuită ρl . Deci:
Q l h ⋅ = Σ ρ şi egalând cu (3) ε 0 E( r)
⋅2π ⋅r
⋅h
= l h ⋅ ρ ceea ce
ρ l
conduce la E ( r)
= = E (8)
G
2π
ε 0 r
2.5. Sarcina uniform distribuită pe suprafaţa unui
conductor cilindric foarte lung de rază „a”
Rezolvarea seamănă cu cele prezentate la punctul 2.4
(figura 5). Metoda aplicată şi aici este tot utilizarea legii
fluxului electric (sau teorema lui Gauss pentru cazul vidului).
Pentru a putea să facem comparaţie între rezultatele obţinute
în cele două situaţii vom considera o echivalenţă privind
încărcarea cu sarcină electrică . O aceeaşi lungime, h, din
cele două conductoare trebuie să conţină o aceeaşi sarcină
electrică, fie că ea este uniform distribuită pe fir cu densitatea
(7)

lineară ρl sau este distribuită uniform, cu densitatea ρS , pe suprafaţa laterală a unui cilindru conductor de
rază „a”, foarte lung (presupus infinit lung).
Se poate stabili astfel o corespondenţă între ρl şi ρS.
ρl
ρl
⋅ h = ρ S ⋅2π
a ⋅ h ; ρ S =
(9)
2π
a
Aplicând legea fluxului electric: D⋅ dS
= Q ∫Σ
Σ
r r
r
D
r
dS
=
r r r r r r
D ⋅ dS
+ D ⋅ dS
+ D ⋅ dS
= 0 + 0 + D ⋅ dS ⋅1
= D dS = D ⋅ 2π
⋅ r ⋅ h
∫ ⋅ ∫ ∫ ∫ ∫ ∫
Σ
S1
S 2
Slat
Slat Slat
ρ S ⋅ 2πah
a
iar QΣ = 2 π ⋅ a ⋅ h ⋅ ρ S
D( r)
= = ρ S ⋅
(9)
2π
r h r
Dacă în această expresie se înlocuieşte densitatea de sarcină distribuită pe suprafaţă cu valoarea
a ρ l a ρ l
echivalentă (9) se obţine: E( r)
= ρ S ⋅ = ⋅ = , expresie identică cu (8).
ε 0r
2π
a ε 0r
2π
ε 0 r
2.6. (SUPLIMENTAR) Sarcina electrică distribuită pe un conductor (metalic) cilindric de lungime
finită “l” şi rază “a” Această punere a problemei nu poate fi rezolvată “exact” cu metode integrodiferenţiale,
de calcul analitic.Rezolvarea se poate face utilizând MEF, programul Qfield. Pentru cei
interesaţi un model al acestei probleme se găseşte în fişierele L306.
3. MODELAREA UNOR CONDENSATOARE
3.1.Considerente teoretice
Condensatorul electric se defineşte ca fiind un ansamblu de două corpuri conductoare (armături metalice)
încărcate cu sarcini electrice egale în modul, dar de semn opus. Între armături se stabileşte un câmp
electrostatic complet (nu există decât linii de câmp ce pornesc de pe armătura pozitivă şi care, toate, se
termină pe armătura negativă, adică nu există linii de câmp care să unească una din armături cu un alt
corp sau cu „infinitul”).
Un caz particular este cel în care
condensatorul este alcătuit din armături
plane şi paralele. În cazul când armăturile
plane au forma identică (indiferent de
formǎ) şi sunt plasate “faţă în faţă”,
condensatorul se numeste condensator plan.
Pentru acest condensator, cu anumite
aproximări care vor fi puse în evidenţă în
cadrul lucrării, este valabilă formula
capacitaţii condensatorului plan (cunoscută
Figura 7.
încă din liceu);
ε 0 ⋅ ε r ⋅ S
C =
(10)
d
formulă în care ε0 este permitivitatea absolută a vidului, εr este permitivitatea relativă a materialului
dielectric care umple complet spaţiul dintre armături, S este suprafaţa (identică) a armăturilor plasate „faţă
în faţă”, iar d este distanţa între cele două armături paralele. Condensatorul cilindric ideal este alcătuit din
doi cilindri concentrici (figura 8), între care se stabileşte o diferenţă de potenţial V1 – V2 . Pentru ca între
armătura centrală şi cea exterioară să se stabilească un câmp electric complet trebuie ca armătura
exterioară să fie la potenţial 0. În caz contrar vor exista şi linii de câmp care vor pleca către ∞ (dacă V2 >
0) sau se vor închide la armǎtura exterioară venind de la ∞ (dacă V2 < 0) şi, în ambele, cazuri acestea vor
aparţine mediului exterior condensatorului, existând câmp şi deci şi energie în afara spaţiului din
interiorul condensatorului.
În cazul general, indiferent de geometria condensatorului (dimensiuni diferite şi formă diferită
pentru cele douǎ armǎturi, poziţia lor relativǎ oarecare) şi de proprietǎţile mediului dintre armǎturi
capacitatea electică a sa se calculează cu formula (11) :
4

C
Q
+ = cu V1 > V2 (11)
V1
−V2
Q+ este sarcina electrică a armăturii pozitive, adică aici Q1 , unde V1 > V2
V1 şi V2 sunt potenţialele armăturii pozitive şi,
respectiv, negative a condensatorului. Reamintim că
V1 nu trebuie să fie neapărat pozitivă şi nici V2 nu
trebuie să fie, neapărat, negativă, ci doar V1 > V2 ,
doar că, aşa cum am arătat anterior, între o armătură
cu potenţial nenul si un alt corp metalic (sau ∞) se
stabileşte un câmp exterior. Acestui câmp exterior îi
corespunde o capacitate parazită (în general de zeci
sau de sute de ori mai mică decât capacitatea
principală) , care poate fi neglijată în multe cazuri,
dar nu intotdeauna.
Formula generală de calcul a capacităţii (11)
este evident valabilă şi în cazul particular al unui
condensator cilindric. Pentru cazul particular, ideal,
prezentat în figura 8, se poate determina o formulă de
Figura 8
Figura 9
calcul a capacităţii ce ţine seama de geometria
condensatorului şi de proprietăţile de material,
presupunând cǎ întregul câmp este concentrat între armǎturi (se neglijeazǎ efectul de capǎt ).
Pentru efectuarea calculelor ne referim la figura 8. Condensatorul cilindric, presupus ideal, are razele
armăturilor R1 şi R2 , înăţimea H şi mediul dielectric dintre armături este aerul (ε = ε0 sau εr = 1). Ţinând
seama de simetria condensatorului legea fluxului electric se aplică pe o suprafaţă cilindrică, Σ ,de o rază
curentă, oarecare, dar R1 < r < R2 şi înălţime h.
Aplicând legea fluxului electric : ∫ D ⋅ dS
= QΣ
Σ
r r
r r r r r r r r
D ⋅ dS
= D ⋅ dS
+ D ⋅ dS
+ D ⋅ dS
=
∫ ∫
Σ
S
1
∫
Slat Slat
S
Slat
= 0 + 0 + ∫ D ⋅ dS ⋅1
= D ∫dS
= D ⋅ 2π
⋅ r ⋅ h
2
∫
Q1
h
iar QΣ = ⋅ 2π
⋅ R1
⋅ h = Q+
⋅
(14)
2πR1
H
H
În relaţia 12 integrala pe suprafaţa închisă Σ a fost descompusă în trei integrale. Integralele pe cele două
baze ale suprafeţei cilindrice Σ sunt nule, pentru că D şi dS sunt ortogonali şi deci produsul lor scalar este
0 (cos π/2 = 0).Pe suprafaţa laterală a cilindrului vectorii D şi dS sunt omoparaleli (aceeaşi direcţie şi
acelaşi sens) şi, din motive de simetrie, în orice punct aparţinând suprafeţei laterale a cilindrului modulul
vectorului D este acelaşi, motiv pentru care a putut fi scos în afara semnului de integrare. În relaţia (14)
sarcina din interiorul suprafeţei Σ se găseşte doar pe porţiunea din suprafaţa laterală a armăturii interioare
“interceptată” de suprafaţa Σ. Din egalarea relaţiilor (13) şi (14) rezultă:
Q+
1
Q+
1
D = ⋅ şi pentru că D = ε 0 ⋅ E , rezultă E = ⋅
(15)
2π
⋅ H r
π ⋅ε
⋅ H r
2 0
Se poate acum calcula tensiunea electrică între cele două ărmături, în funcţie de sarcină:
U
1,
2
= V
1
−V
2
1
1
1
0
(12)
(13)
R2
R2
R
r
2
r
Q+
1 Q+
R
= ∫E⋅dr= ∫E⋅dr = ∫ ⋅ dr = ⋅ ln
2π
⋅ε
⋅ H r 2π
⋅ε
⋅ H R
R
R
R
şi pentru capacitatea electrică a condensatorului cu armăturile de formă cilindrică, coaxiale, rezultă
2π
⋅ε
0 ⋅ H
C =
R
(17)
2
ln
R
1
5
0
2
1
(16)

4.PARTEA PRACTICA.
4.1. Calculul unor valori ale câmpului cu ajutorul unor expresii determinate analitic
x = 1 m x = 3 m Se completează datele din tabel utilizând formulele adecvate.
E1P V/m
Semnificaţiile şi expresiile intensităţii câmpului în punctul P au fost
E3P
EiP
E∞P
EGP
V/m
V/m
V/m
V/m
precizate la paragrafele 2.1. ... 2.4.
Aceste calcule se fac în cadrul laboratorului, măcar parţial.
Fiecare student trebuie să aibă calculate cel puţin 4 valori, pe care le
trece în tabel. Restul calculelor pot fi efectuate acasă, verificarea lor
având loc odată cu lucrarea L7 (de încheiere a activităţii de laborator).
4.2. Modelarea unui condensator plan ideal cu armături dreptunghiulare.
Problema modelată este L301.
a) Se fixează valoarea tensiunii între armături la valoarea de 10V (se intervine în Data). Valoarea
potenţialului armăturii pozitive se ia V1 = +G volţi, G fiind numarul grupei din care face parte studentul.
EA V/m VA V
EB V/m VB V
b) Se notează datele geometrice ale condensatorului
modelat; S – aria armăturilor şi d – distanţa între
armături
EC V/m VC V
c) Se preiau din programul Qfield valorile câmpului
electric şi ale potenţialului electric în puncte situate pe linia mijlocie ce uneşte cele două armături. Punctul
A este situat la jumătatea distanţei între armături, punctul B este situat mai aproape de armătura pozitivă,
la ¼ din distanţa dintre armături şi apoi punctul C este situat la ¾ din distanţa dintre armături, distanţă
măsurată faţă de armătura pozitivă. Se va prezenta poziţia punctelor pe un desen calitativ. Se scriu
valorile EA, EB şi EC , respectiv, VA, VB B şi VC
în referat.
d) Se calculeaza teoretic valoarea condensatorului modelat
SUPLIMENTAR
e) Se modifică distanţa dintre armături, apropiindu-le cu câte 50mm faţă de centru fiecare (pentru a păstra
simetria) şi se constată creşterea valorii câmpului electric.
SE LUCREAZA IN L305. NU MODIFICATI L301!
f) Se modifică condiţiile de frontieră, lasând câmpul electric să iasă din spaţiul dintre armături (L307). Se
poate observa ca în interiorul armăturilor câmpul nu mai este riguros uniform şi că în exterior campul este
cu atât mai important cu cât armăturile sunt mai îndepărtate
4.3. Modelarea unui codensator coaxial cilindric cu armăturile de raze R1 şi R2.
Modelarea acestei probleme se poate face , în 2D, în două moduri.
Se poate face o secţiune în lungul
axei de simetrie a problemei (axa
cilindrilor coaxiali). Aşa este
prezentat în figura 10. Se remarcă
direcţia radială a liniilor de câmp ,
precum şi faptul că modulul
vectorului intensitate a câmpului
electric este mai mare în apropierea
armăturii interioare şi este mai mic
pe măsură cene îndepărtăm de
aceasta.
De asemenea este foarte important
de remarcat că intensitatea câmpului
electrostatic este zero în interiorul
corpurilor metalice (armăturile
condensatorului). Din acest motiv grosimea armăturii exterioare nu contează, ea neinfluenţând asupra
felului cum este distribuit câmpul electric, localizat între armături.
a). Să se reprezinte, calitativ, variaţia câmpului electric E, în lungul razei, prin centrul
condensatorului. Linia de reprezentare se alege între punctele de coordonate : z = 500 mm, r = 0 şi z =
500 mm şi r = 500mm. Se notează valorile R1 şi R2 .
6

Se reprezintă intensitatea câmpului şi în interiorul armăturilor metalice (E = 0).
b) Se reprezintă, calitativ, variaţia potenţialului, în lungul aceleiaşi linii.
c) Să se noteze valoarea intensităţii în punctul situat la mijlocul distanţei dinte armături şi valoarea
potenţialului în acelaşi punct.
d) Se calculează teoretic valoarea capacotăţii condensatorului modelat
Modelarea se poate face şi printr-o secţiune perpendiculară pe axa de simetrie a condensatorului, secţiune
efectuată în centrul (zona centrală) condensatorului
SUPLIMENTAR.
e) Se vizualizează elementele corepunzătoare problemei L303 (modelare a secţiunii perpendiculare pe axa
de simetrie a condensatorului). Se pot urmari şi aici cele de la 4.3.a,b şi c.
f) Se poate urmări în problema L304 felul cum a fost modelat un condensator sferic. Se poate înţelege că
din considerente de simetrie a putut fi făcută reprezentarea doar a unui sfert din secţiunea prin sferă. Se
pot urmări vectorii de cămp şi reprezentarea (Plot) în funcţie de rază a diferitelor mărimi.
In toate cazurile modelate se poate calcula capacitatea electrică a condensatorului modelat.
TEME OBLIGATORII
6. Condensatorul plan reprezentat în problema L301 (punctul 4.2) are dielectric arerul şi este alimentat cu
tensiunea de 25V. Distanţa dintre armături este 40 mm, iar armăturile au dimensiunile 0,4·π m x 72N cm
6.1. Să se calculeze capacitatea condensatorului C0 exprimată în pF
6.2. intensitatea câmpului electric E0 în punctul central al condensatorului
6.3. densitatea de sarcină ρ0 de pe armătura pozitivă
Dacă se introduce între armături un bloc dielectric papalelipipedic, cu permitivitatea relativă 4, care ocupă
complet spaţiul dintre armături, păstrând aceeaşi diferenţă de potenţial între armături, să se calculeze:
6.4. capacitatea condensatorului C4,
6.5. intensitatea câmpului E4 în punctul central al condensatorului
6.6. densitatea de sarcină ρ4 de pe armătura pozitivă
Se deconectează de la sursă condensatorul cu dielectricul între armaturi şi, după deconectare, se scoate
parţial dielectricul dintre armaturi. Considerând că acum dielectricul ocupă jumătate din volum, iar
cealaltă jumătate este ocupată de aer, precum şi considerând că întregul câmp electrostatic este concentrat
în volumul dintre armături, să se deseneze schematic condensatorul neomogen şi să se calculeze:
6.7. capacitatea condensatorului C1/2
6.8. tensiunea la bornele condensatorului U1/2
6.9. densitatea de energie in volumul ocupat de aer
Răspunsurile la întrebările 6.1. .....6.9. se predau cu ocazia efectuării următoarei lucrări
PROBLEME SUPLIMENTARE
7. Să se calculeze analitic capacitatea teoretică a condensatoarelor cilindric şi sferic, modelate, şi să se
compare cu rezultate obţinute folosind Qfield.
8. Să se calculeze densitatea de sarcină pe armăturile condensatorului cilindric ideal, modelat
9. Să se calculeze energia înmagazinată în fiecare din condensatoarele modelate, daca tensiunea aplicată
este de 10V.
7