1 Zur Lagrange-Multiplikatoren - TUM M7/Analysis

Studentische Fragen zur HM2-Übung, Blatt 5
Autor: Yuen Au Yeung Stand: 25.05.2012
Guide: Hier sind Fragen und Antworten aufgelistet, die mir vor/während/nach meinen drei
wöchentlichen Übungen gestellt wurden. Fragen wurden in blau, Antworten in rot hervorgehoben.
Bei langen Fragen wurden die Stichwörter in rosa geschrieben. Nachträgliche Korrekturen
in den Antworten sind ebenfalls rot markiert.
1 Zur Lagrange-Multiplikatoren
1. Frage: Was bedeutet anschaulisch, dass die Gradienten der zu minimierenden Funktion
und der Nebenbedingungsfunktion an einer Extrenalstelle unter Nebenbedingung zueinander
parallel sind?
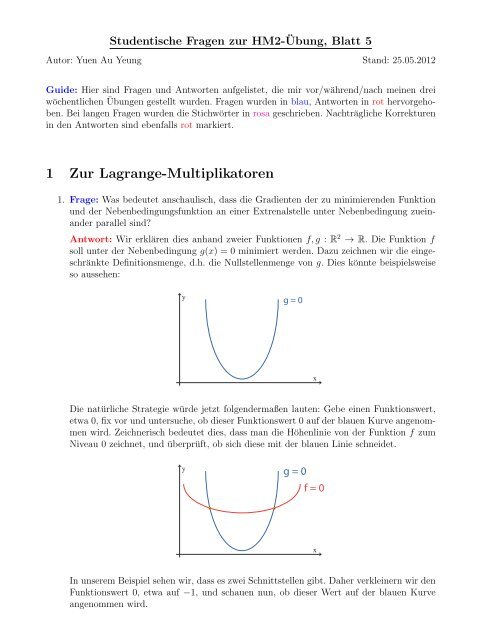
Antwort: Wir erklären dies anhand zweier Funktionen f, g : R 2 → R. Die Funktion f
soll unter der Nebenbedingung g(x) = 0 minimiert werden. Dazu zeichnen wir die eingeschränkte
Definitionsmenge, d.h. die Nullstellenmenge von g. Dies könnte beispielsweise
so aussehen:
y
g = 0
Die natürliche Strategie würde jetzt folgendermaßen lauten: Gebe einen Funktionswert,
etwa 0, fix vor und untersuche, ob dieser Funktionswert 0 auf der blauen Kurve angenommen
wird. Zeichnerisch bedeutet dies, dass man die Höhenlinie von der Funktion f zum
Niveau 0 zeichnet, und überprüft, ob sich diese mit der blauen Linie schneidet.
y
g = 0
x
f = 0
In unserem Beispiel sehen wir, dass es zwei Schnittstellen gibt. Daher verkleinern wir den
Funktionswert 0, etwa auf −1, und schauen nun, ob dieser Wert auf der blauen Kurve
angenommen wird.
x

y
g = 0
f = 0
f = -1
Wir zeichnen sukzessive die Höhenlinien (=Niveaulinien) zu einem noch kleineren Funktionswert
von f ein und hören genau dann auf, wenn eine Verkleinerung keinen Schnittpunkt
mehr mit der blauen Kurve hat. Diese Stelle ist nun also unsere Minimalstelle
von f, eingeschränkt auf der blauen Kurve. Wenn wir jetzt die Tatsache berücksichtigen,
dass Gradienten an einer Stelle stets senkrecht auf Höhenlinien der Funktionen stehen
(siehe Skript S. 148f.), erhält man folgende Zeichnung, in der tatsächlich die Gradienten
zueinander parallel sind.
y
g = 0
x
f = 0
f = -1
f = -2
f = -5
Man könnte jetzt einwenden, dass die Höhenlinien bei Verkleinerung der Funktionswerte
von f nicht absteigend vorkommen. Es könnte auch sein, dass die Höhenlinie des Funktionswertes
-1 zwischen den Höhenlinien des Funktionswertes 0 liegt:
y
g = 0
x
f = 0
f = -1
In diesem Fall besitzt aber f (aus Stetigkeitsgründen!) ein lokales Minimum an den grünen
Schnittpunkten, weil die Funktionswerte unmittelbar überhalb und unterhalb der Niveaulinie
f = −1 wieder zunehmen. Man beachte, dass dieses lokale Minimum auch ohne
Nebenbedingung auftritt.
Der Gradient von f ist demzufolge an den grünen Stellen der Nullvektor und die Gleichung
f = 0
∇f(grüne Stelle) + λg(grüne Stelle) = 0
ist für λ = 0 erfüllt – völlig unabhängig davon, in welche Richtung ∇g(grüne Stelle) zeigt.
x

2. Frage: In der Zentralübung haben wir die stationären Punkte der Lagrange-Funktion
untersucht. Wieso hier nicht?
Antwort: Weil es dasselbe ist! Die Lagrange-Funktion lautet L( −→ x ) = f( −→ x ) + λg( −→ x ).
Die stationären Punkte von L erfüllen alle
∇L( −→
∇xf(
x , λ) =
−→ x ) + λ∇xg( −→ x )
g( −→
0
=
x )
0
Das ∇L ist der Gradient von L und enthält alle partiellen Ableitungen nach xi und nach
λ. Das ∇x soll nur andeuten, dass wir nur alle partiellen Ableitungen nach xi betrachten.
3. Frage: Wenn die Menge, auf der ich eine Funktion maximiere bzw. minimiere, offen ist,
brauche ich kein Lagrange, oder?
Antwort: Genau! Dann wird klassisch via stationären Punkten und Definitheit des Hesse-
Matrix untersucht.
4. Frage: Zur Kompaktheit: Ist eine abgeschlossene Menge ín R n nicht automatisch beschränkt?
Antwort: Nein. Zum Beispiel ist R n abgeschlossen, aber unbeschränkt. Das halboffene
Intervall [0, ∞[ ist abgeschlossen in R. Das kann man folgendermaßen erklären (wird jetzt
etwas technisch):
Eine Teilmenge A ⊂ R n heißt offen, wenn man in jedem beliebigen Punkt von A eine
Kugel mit einem geeignet kleinen Radius legen kann, sodass die Kugel noch vollständig
in der Menge enthalten ist. Wie groß der Radius ist, ist egal – es kommt nur darauf an,
dass es einen solchen gibt.
Eine Menge A ⊂ R n heißt abgeschlossen, wenn ihr Komplement R n \A offen ist.
Wir schauen uns die Menge A = [0, ∞[ an; sie ist abgeschlossen. Denn Ihr Komplement
ist ] − ∞, 0[. Das sind alle negative Zahlen. Man kann um jeder negativen Zahl ein kleines
Intervall 1 legen, welches nur negative Zahlen enthält.
2 Zu impliziten Funktionen
1. Frage: Was meinst du mit fx(x, y, g(x, y)) und fz(x, y, g(x, y))?
Antwort: Wir greifen auf die Funktion in der H 5.3 zurück. Dort war
f(x, y, z) = z 3 − z + 3x 2 + 2y 2 .
Es war (0, 0) ein stationärer Punkt von g und g(0, 0) = −1. Wir berechnen gxx(0, 0)
explizit. Nach der Tutorübung gilt:
gxx(0, 0) = − fxx(0, 0, g(0, 0))
fz(0, 0, g(0, 0)) .
Die partiellen Ableitungen nach x und z lauten:
Also ist
fxx(x, y, z) = 6, fz(x, y, z) = 3z 2 − 1.
6
gxx(0, 0) = −
3g(0, 0) 2 6
= −
− 1 3 · (−1) 2 = −3.
− 1
1 Intervall ist das eindimensionale Pendant zur Kugel.