7. Quadratische Funktionen lineare Funktion: y = f (x) = ax + b Graph ...
7. Quadratische Funktionen lineare Funktion: y = f (x) = ax + b Graph ...
7. Quadratische Funktionen lineare Funktion: y = f (x) = ax + b Graph ...
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
<strong>7.</strong> <strong>Quadratische</strong> <strong><strong>Funktion</strong>en</strong><br />
<strong>lineare</strong> <strong>Funktion</strong>: y = f (x) = <strong>ax</strong> + b <strong>Graph</strong>: Gerade mit der Steigung a und dem y-<br />
Achsenabschnitt b<br />
quadratische <strong>Funktion</strong>: y = f (x) = <strong>ax</strong> 2 + bx + c <strong>Graph</strong>: Parabel, sofern a ≠ 0<br />
Es wird im Folgenden untersucht, wie die Parameter<br />
a, b, c interpretiert werden können.<br />
Spezialfälle:<br />
a) y = f (x) = <strong>ax</strong> 2 Skizze: a = 1, 2 , 1 /4 , - 1 /4<br />
Satz:<br />
Der <strong>Graph</strong> der <strong>Funktion</strong> f: x → y = <strong>ax</strong> 2 , a ≠ 0<br />
(Die Kurve mit der Gleichung y = <strong>ax</strong> 2 ) heisst<br />
quadratische Parabel. Die y-Achse ist Symmetrieachse,<br />
der Nullpunkt Scheitelpunkt der Parabel. Die Parabel ist<br />
für a > 0 nach oben, für a < 0 nach unten geöffnet. Der<br />
Parameter a bewirkt eine Dehnung oder Pressung der<br />
Normalparabel y = x 2 in y-Richtung im<br />
Verhältnis a:1 (normale Affinität zur x-Achse).<br />
Hinweis:<br />
Eine Ellipse ist das normalaffine Bild eines Kreises.<br />
Aufgabe:<br />
Bestimme den Parameter a so, dass die Parabel y = f (x) = <strong>ax</strong> 2 durch den Punkt Q(-3, 6) geht.<br />
Die Koordinaten des Punktes Q erfüllen die Kurvengleichung:<br />
f (-3) = 6 oder 6 = 9a oder also a = 2 /3.<br />
b) y = f (x) = <strong>ax</strong> 2 + c a, c ∈ R, a ≠ 0<br />
Skizze: a = 1 /4<br />
c = 0, -3, 2<br />
Satz:<br />
Der <strong>Graph</strong> der <strong>Funktion</strong> f: x → y = <strong>ax</strong> 2 + c ist eine zur<br />
y-Achse symmetrische Parabel mit dem Scheitel S(0, c).<br />
Sie entsteht aus der Parabel y = <strong>ax</strong> 2 durch Translation<br />
⎛0<br />
⎞<br />
um den Vektor ⎜ ⎟ .<br />
⎝c<br />
⎠<br />
Aufgabe:<br />
Eine zur y-Achse symmetrische Parabel geht durch die Punkte P(4, 2) und Q(2, -1). Bestimme<br />
ihre Gleichung.<br />
f 4 = 2 16a<br />
+ c = 2<br />
( )<br />
( 2)<br />
= −1<br />
4a<br />
+ c = −1<br />
f<br />
y = f(x) = ¼ x 2 - 2<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
1
2<br />
c) y f ( x) <strong>ax</strong> bx x ( <strong>ax</strong> b)<br />
= = + = ⋅ + a, b∈ R, a ≠ 0<br />
In diesem Fall können die Schnittpunkte der Parabel mit<br />
der x-Achse unmittelbar angegeben werden:<br />
b<br />
x1 = 0 und x 2 = − a . Aus Symmetriegründen liegt der<br />
b<br />
Scheitel folglich an der Stelle u = − 2a<br />
. Die y-<br />
Koordinate v ergibt sich dann zu v = f(u).<br />
Skizze : a = ½, b = -2<br />
Scheitel S(2, -2)<br />
Verallgemeinerung :<br />
Liegt die Gleichung in der Form<br />
y = a ⋅( x − x1) ⋅( x − x2)<br />
a ≠ 0<br />
vor, so ergeben sich daraus die x-Koordinaten der beiden Schnittpunkte zu x1 und x2. Aus<br />
x1 + x2<br />
Symmetriegründen ist dann die x-Koordinate des Scheitels u = .<br />
2<br />
d)<br />
Wegen c) ist die x-Koordinate u des Scheitels auch im<br />
allgemeinen Fall bekannt, denn der zusätzliche<br />
Summand c verändert nur die y- Koordinate des<br />
Scheitels.<br />
Beispiel:<br />
1 2<br />
y = f ( x) = 2 ⋅ x − 2x + 3,<br />
a = ½, b = -2, c = 3<br />
Die Parabel entsteht aus der von Beispiel c) durch eine<br />
Translation um 3 in y-Richtung:<br />
Die <strong>Funktion</strong>sgleichung kann durch quadratische<br />
Ergänzung folgendermassen umgeformt werden:<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
( ) ( ) 2<br />
y = f ( x) = ⋅ x − 2x + 3 = ⋅ x − 4x + 4 + 1 = ⋅ x − 2 + 1<br />
1 2 1 2<br />
1<br />
2 2 2<br />
In dieser Form sind die Scheitelkoordinaten S(2, 1) direkt zu erkennen.<br />
Vorgehen im allgemeinen Fall:<br />
b<br />
Wegen c) kann die x-Koordinate des Scheitels angegeben werden u = − 2a<br />
. Die y-Koordinate<br />
erhält man, indem man u in die Parabelgleichung einsetzt: v = f(u).<br />
Illustration am Beispiel<br />
y = f x 1 2<br />
= ⋅ x + x + 4<br />
( )<br />
4<br />
1<br />
x-Koordinate des Scheitels: = − 1 = − 2 v = f(-2) = 3<br />
u 2⋅<br />
4<br />
Es handelt sich also um eine Parabel mit dem Scheitel S(-2, 3). Sie geht aus der Parabel mit<br />
1 2<br />
der Gleichung y = 4 ⋅ x durch eine Parallelverschiebung hervor.<br />
Nach quadratischer Ergänzung ergibt sich die Parabelgleichung in der Form:<br />
( ) ( ) 2<br />
1 2<br />
1<br />
y = f x = ⋅ x + x + 4 = ⋅ x + 2 + 3<br />
Allgemein gilt<br />
4 4<br />
2
Satz:<br />
Der <strong>Graph</strong> der <strong>Funktion</strong> f(x) = <strong>ax</strong> 2 + bx + c ist eine Parabel mit dem Scheitel<br />
⎛ b ⎛ b ⎞⎞<br />
S ⎜ − , f ⎜ − ⎟<br />
2a 2a<br />
⎟<br />
⎝ ⎝ ⎠⎠<br />
. Sie geht aus der Ursprungsparabel mit der Gleichung y = <strong>ax</strong>2 durch eine<br />
Translation hervor. Für a > 0 ist sie nach oben, für a < 0 nach unten geöffnet.<br />
Bemerkung:<br />
Die Form der Parabel wird allein durch den Wert des Parameters a bestimmt. b bzw. c<br />
bestimmen die Lage der Parabel im Koordinatensystem.<br />
Übungsaufgabe:<br />
( ) ( ) 2<br />
1 2 5 1<br />
y = f x = − 2 ⋅ x + x − 2 = − 2 ⋅ x −1 − 2 S(1, -2)<br />
e)<br />
Die Scheitelkoordinaten können auch bestimmt werden, indem man den <strong>Funktion</strong>sterm mit<br />
quadratischer Ergänzung auf die Form ( ) 2<br />
y = a ⋅ x − u + v bringt.<br />
Beispiel:<br />
y = f x =<br />
2<br />
⋅ x − 3x<br />
+<br />
( ) 1<br />
2<br />
1<br />
2<br />
2 ( x x [ ] ) ( x )<br />
= ⋅ − 6 + 9 − 9 + 1 = ⋅ − 3 − 4<br />
1 1<br />
2 2<br />
Die Parabel entsteht aus der mit der Gleichung<br />
y = f x 1 2<br />
= ⋅ x durch eine Parallelverschiebung um<br />
( )<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
2<br />
3 Einheiten in positiver x-Richtung und um 4<br />
Einheiten in negativer y-Richtung hervor.<br />
Lösung im allgemeinen Fall :<br />
2<br />
2 2 2 2<br />
⎛ 2 2 b ⎛ b ⎞ ⎛ b ⎞ ⎞ ⎛⎛ b ⎞ ⎛ b ⎞ ⎞<br />
y = <strong>ax</strong> + bx + c = a ⎜ x + 2⋅ x + − + c = a x + − + c<br />
⎜ ⎜ ⎟ ⎜ ⎟ ⎟ ⎜⎜ ⎟ ⎜ ⎟ ⎟<br />
2a ⎝ 2a ⎠ ⎝ 2a ⎠ ⎟ ⎜⎝ 2a ⎠ ⎝ 2a<br />
⎠ ⎟<br />
⎝ ⎠ ⎝ ⎠<br />
2 2 2 2<br />
2<br />
⎛ b ⎞<br />
= a ⎜ x + ⎟<br />
⎝ 2a ⎠<br />
b 4a ⎛ b ⎞<br />
− + c ⋅ = a⎜ x + ⎟<br />
4a 4a ⎝ 2a ⎠<br />
b<br />
−<br />
− 4ac<br />
⎛ b ⎞<br />
= a⎜ x + ⎟<br />
4a ⎝ 2a ⎠<br />
D<br />
−<br />
4a<br />
⎛ b ⎛ b ⎞ −D ⎞<br />
Für die Scheitelkoordinaten gilt damit: S ⎜u = − , v = f ⎜ − ⎟ =<br />
2a 2a 4a<br />
⎟<br />
⎝ ⎝ ⎠ ⎠<br />
Satz:<br />
2<br />
Der <strong>Graph</strong> der <strong>Funktion</strong> f: x → y = f ( x) = a ⋅( x − u) + v ist eine Parabel mit dem Scheitel<br />
S(u, v). Sie entsteht aus der Parabel mit der Gleichung y = <strong>ax</strong> 2 durch Translation um den<br />
Vektor u ⎛ ⎞<br />
⎜ ⎟<br />
⎝ v ⎠ .<br />
3
8. Zusammenhang zwischen quadratischer <strong>Funktion</strong> und Gleichung<br />
1 2<br />
In der Skizze sind die Parabeln y = 2 ⋅ x − x + c für die Parameterwerte<br />
a) c = 2 b) c = 1 /2 und c) c = -2 dargestellt. Die Parabeln gehen durch Parallelverschiebung in<br />
y-Richtung auseinander hervor. Die Bestimmung der Schnittpunkte der Parabel mit der<br />
1 2<br />
x-Achse führt auf die quadratische Gleichung ⋅ x − x + c = 0<br />
a) c = 2 Diskriminante D < 0<br />
die Parabel meidet die x-Achse<br />
b) c = 1 /2 D = 0: genau eine Lösung<br />
die Parabel berührt die x-Achse<br />
c) c = -2 D > 0: zwei reelle Lösungen<br />
die Parabel schneidet die x-Achse<br />
Schreibt man die quadratische Auflösungsformel in der<br />
−b<br />
D<br />
Form x1,2<br />
= ± so sieht man, dass sich im Fall<br />
2a 2a<br />
D > 0 die beiden Lösungen x1 ,2 ergeben, indem man von der x-Koordinate des Scheitels 2<br />
D<br />
ausgehend<br />
2a<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
addiert bzw. subtrahiert.<br />
Allgemein:<br />
(1) quadratische Gleichung <strong>ax</strong> 2 + bx + c = 0 mit der Diskriminante D<br />
(2) zugehörige quadratische <strong>Funktion</strong> y = f(x) = <strong>ax</strong> 2 + bx+ c<br />
a) D < 0 Gleichung (1) hat keine reelle Lösung<br />
die quadratische Parabel (2) meidet die x-Achse<br />
b) D = 0 Gleichung (1) hat genau eine reelle Lösung<br />
die quadratische Parabel (2) berührt die x-Achse<br />
c) D > 0 Gleichung (1) hat zwei reelle Lösungen<br />
die quadratische Parabel (2) schneidet die x-Achse<br />
2<br />
− b<br />
a<br />
4
9. <strong>Quadratische</strong> Ungleichungen<br />
<strong>Quadratische</strong> Ungleichungen können gelöst werden, indem man die zugehörige quadratische<br />
<strong>Funktion</strong> betrachtet. Die Lösungsmenge ergibt sich dann, indem man die Schnittpunkte des<br />
<strong>Graph</strong>en mit der x-Achse bestimmt und deren Öffnung berücksichtigt.<br />
Illustration an Beispielen:<br />
a) x 2 + 2x - 3 < 0<br />
Der <strong>Graph</strong> der zugehörigen quadratischen <strong>Funktion</strong><br />
f(x) = x 2 + 2x – 3 = (x + 3)⋅(x - 1) ist eine nach oben<br />
geöffnete Parabel, welche die x-Achse an den Stellen<br />
x1 = 1 und x2 = -3 schneidet. Die Parabel verläuft im<br />
Intervall ]-3/1[ unterhalb der x-Achse, das heisst dort<br />
f(x) < 0 ist. Lösungsmenge L = ]-3/1[<br />
Bemerkung:<br />
Die Lösungsmenge L kann auch mit einer<br />
Fallunterscheidung gelöst werden. L besteht aus den reellen<br />
Zahlen für die einer der Faktoren negativ und der andere positiv<br />
ist.<br />
Äquivalenzumformungen bei Ungleichungen:<br />
Die Lösungsmenge einer Ungleichung ändert sich nicht, wenn<br />
man<br />
• auf beiden Seiten dieselbe Zahl addiert (subtrahiert)<br />
• beide Seiten mit derselben positiven Zahl multipliziert.<br />
b) - ¼ x 2 + x + 3 ≤ 0<br />
Hilfsfunktion f(x) = - ¼ x 2 + x + 3<br />
Lösungsmenge L = ]-∞ , -2] ∪ [6 , ∞[<br />
x − 2<br />
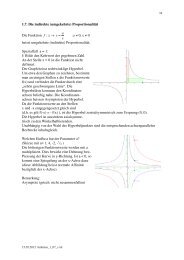
c) > 0<br />
x + 1<br />
Eine Fallunterscheidung lässt sich vermeiden, indem man mit dem Quadrat des Nenners<br />
multipliziert.<br />
Die neue Ungleichung (x - 2)⋅(x + 1) > 0 hat die Lösungsmenge L = ]-∞ , -1[ ∪ ]2, ∞[<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
5
Aufgabe:<br />
Beschreibe die gefärbte Punktmenge in der Abbildung<br />
(ohne Rand) durch ein System von Ungleichungen.<br />
Da die Parabel die x-Achse an den Stellen<br />
x = 0 und x = 4 schneidet, kann ihre Gleichung in der<br />
y = <strong>ax</strong> ⋅ x − 4 angesetzt werden.<br />
Form ( )<br />
Der Scheitel S(2, 4) erfüllt die Parabelgleichung:<br />
4 = a ⋅ 2⋅ 4 − 2 mit der Lösung a = ½.<br />
( )<br />
Gesuchtes Ungleichungssystem:<br />
1<br />
2<br />
( 4 )<br />
y < x − x<br />
y > 2 − x<br />
1<br />
2<br />
10. Parabelgleichung gesucht<br />
Aufgabe:<br />
Bestimme eine Gleichung der Parabel mit den angegebenen Eigenschaften:<br />
a) wenn der Scheitel S(3, 4) und der Parabelpunkt A(-1, 0) gegeben sind.<br />
b) wenn die Parabelpunkte A(2, 5), B(4, 4) und C(-2, 1) gegeben sind.<br />
a)<br />
2<br />
Ansatz: y = f ( x) = a ⋅( x − 3) + 4<br />
A erfüllt die Gleichung oder f(-1) = 0<br />
( ) 2<br />
a − 1+ 3 + 4 = 0 ergibt a = - 1 /4<br />
Gesuchte Gleichung:<br />
b)<br />
y = f x = <strong>ax</strong> + bx + c<br />
Ansatz: ( ) 2<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
y = f x = − ⋅ x − +<br />
1<br />
2<br />
( ) 4 ( 3) 4<br />
Die drei Parabelpunkte erfüllen die Parabelgleichung:<br />
f 2 = 5 4a<br />
+ 2b<br />
+ c = 5 ⋅(<br />
−1)<br />
⋅1<br />
f<br />
( )<br />
( 4)<br />
= 4 16a<br />
+ 4b<br />
+ c = 4 ⋅1<br />
( − 2)<br />
= 1 4a<br />
− 2b<br />
+ c = 1 ⋅(<br />
−1)<br />
f<br />
12 2 1<br />
4 1<br />
a + b = − a = −<br />
4b<br />
= 4 b = 1<br />
Mit dem Additionsverfahren ergibt sich die Lösung<br />
y = f(x) = - 1 /4 x 2 + x + 4<br />
6
Aufgabe:<br />
Gemäss einer Faustformel gilt für die Anhaltestrecke eines Autos bei nasser Strasse<br />
2<br />
b v = cv + dv<br />
( )<br />
b(v) bezeichnet die Anhaltestrecke in Meter, v die Geschwindigkeit in km/h, c, d sind<br />
Konstanten.<br />
Man weiss, dass b(80) = 70 b(100) = 105<br />
Wie gross ist b(130)?<br />
80c + 6400d = 72<br />
100c + 10000d = 105<br />
b(130) ≈130.65 m<br />
11. Die Parabel als geometrischer Ort<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
Lösung d = 3 /10, d = 3 /400<br />
Aufgabe:<br />
Bestimme die Menge aller Punkte der Ebene, die von einem festen Punkt F<br />
und einer gegebenen Geraden l gleichen Abstand haben.<br />
Bezeichnungen:<br />
l heisst Leitgerade, F Brennpunkt,<br />
der Abstand des Brennpunkts F<br />
von der Leitgeraden l heisst Para-<br />
Meter und wird mit p bezeichnet.<br />
Skizze:<br />
l: y = -1 F(0,1)<br />
Konstruktion:<br />
Schneide die Parallele zur Leitgeraden im<br />
Abstand r mit dem Kreis um F mit<br />
Radius r.<br />
Ortsbedingung:<br />
2 2<br />
2 2 ⎛ p ⎞ ⎛ p ⎞ 2<br />
PL = PF ⎜ y + ⎟ = ⎜ y − ⎟ + x nach Pythagoras, vereinfacht zu<br />
⎝ 2 ⎠ ⎝ 2 ⎠<br />
2<br />
x 2<br />
(1) y = = <strong>ax</strong> Gleichung der Parabel mit dem Brennpunkt F(0, ½ p)<br />
2 p<br />
und der Leitgeraden l: y = - ½ p<br />
Aufgabe:<br />
Berechne für die Ursprungsparabel y = x 2 die Koordinaten des Brennpunkts.<br />
1<br />
Zusammenhang zwischen a und p nach (1): a =<br />
2 p<br />
Für die Normalparabel mit a = 1 ergibt sich p zu p = ½.<br />
Koordinaten des Brennpunkts F(0, ¼)<br />
7
Für technische Anwendungen ist die folgende Parabeleigenschaft wichtig:<br />
Achsenparallel einfallendes Licht wird an einem parabolförmigen Spiegel nach dem<br />
Brennpunkt reflektiert (Parabolspiegel, Parabolantenne).<br />
Übungsaufgabe:<br />
a)<br />
Auf welcher Kurve liegen die Mittelpunkte M(x, y) der Kreise, die durch den Punkt C(2,1)<br />
gehen und die x-Achse berühren?<br />
1 2 5<br />
Lösung: y = 2 x − 2x<br />
+ 2<br />
b) Über der Grundseite A(-c, 0)B(c, 0) werden Dreiecke betrachtet, deren Ecke C auf der<br />
Geraden y = h mit h > 0 liegen. Auf welcher Kurve liegen die Höhenschnittpunkte dieser<br />
Dreiecke?<br />
Lösung:<br />
2<br />
1 2 c<br />
y = − ⋅ x +<br />
h h<br />
12. Extremalaufgaben<br />
Beispiele:<br />
a)<br />
Dem Rechteck mit den Seiten a = 5 und b = 3 wird ein<br />
Parallelogramm einbeschrieben. Für welche Wahl von x<br />
wird der Parallelogramminhalt I minimal?<br />
Zielfunktion: Der Parallelogramminhalt soll minimal<br />
werden:<br />
I(x) = 15 - x⋅(3 - x) - x⋅(5 - x) = 2x 2 - 8x+ 15<br />
Bestimmung des Extremums:<br />
Der <strong>Graph</strong> der <strong>Funktion</strong> I ist eine nach oben geöffnete<br />
Parabel. Die Scheitelkoordinaten ergeben sich zu u = 2 bzw. v = I(2) = 7<br />
Ergebnis:<br />
Der Inhalt des Parallelogramms wird für x = 2 minimal. Der minimale Inhalt beträgt I(2) = <strong>7.</strong><br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
8
)<br />
Eine Fabrik setzt monatlich 200 Stück eines Zubehörteils ab und hat an jedem Stück einen<br />
Reingewinn von 10 Fr.. Marktforschung hat ergeben, dass eine Preissenkung von Fr. 1.-,<br />
Fr 2.-, usf. eine Erhöhung des Monatsumsatzes von c = 50 Stück, 2c Stück bewirken würde.<br />
Bei welcher Preissenkung pro Stück ist der grösste Gesamtgewinn zu erwarten?<br />
Zielfunktion:<br />
Gewinn in Fr. pro Stück bei einer Preisreduktion um x Fr.: 10 - x<br />
Anzahl verkaufte Stücke 200 + 50x<br />
Gesamtgewinn G ( x)<br />
= ( 10 − x)<br />
⋅(<br />
200 + 50x)<br />
= 50 ⋅ ( 10 − x)<br />
⋅(<br />
4 + x)<br />
Bestimmung des Extremums:<br />
Der <strong>Graph</strong> der Zielfunktion ist eine nach unten geöffnete Parabel, welche die x-Achse an den<br />
Stellen 10 und -4 schneidet. Der Scheitel liegt damit aus Symmetriegründen an der Stelle<br />
x = 3.<br />
Der Gesamtgewinn wird bei einer Preisreduktion von Fr. 3.- m<strong>ax</strong>imal und beträgt<br />
G(3) = 2450 Fr.<br />
c)<br />
Eine ebene 400 m-Bahn soll so angelegt werden, dass sie ein Rechteck mit zwei angesetzten<br />
Halbkreisen begrenzt. Wie gross muss der<br />
Radius r sein und wie lang ein gerades Stück<br />
zwischen den Kurven, wenn das Rechteck<br />
m<strong>ax</strong>imalen Flächeninhalt haben soll?<br />
A( r)<br />
= 2r<br />
⋅ ( 200 − πr)<br />
Der Inhalt des Rechtecks ist bei<br />
100<br />
r = m m<strong>ax</strong>imal.<br />
π<br />
Länge des geraden Stücks 100 m.<br />
Bemerkung:<br />
Die Bestimmungen des IAAF schreiben für die Geraden eine Länge von 84.39 Meter und für<br />
den Kurvenradius 36.80 Meter vor.<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
9
In den folgenden Beispielen treten sogenannte Nebenbedingungen auf:<br />
d)<br />
Von einer rechteckigen Glasplatte von 15 dm<br />
und b = 12 dm ist an einer Ecke ein Stück in<br />
Form eines rechtwinkligen Dreiecks mit den<br />
Katheten c = 6 dm und d = 4 dm<br />
abgebrochen. Aus der restlichen Platte soll<br />
eine rechteckige Platte von möglichst<br />
grossem Flächeninhalt geschnitten werden.<br />
Bestimme Länge und Breite dieses<br />
Rechtecks.<br />
1. Zielfunktion: Flächeninhalt A minimal<br />
A = ( 15 − x)<br />
⋅(<br />
12 − y)<br />
2. Nebenbedingung : (Geradengleichung oder Strahlensatz)<br />
2 y = − 3 x + 4<br />
3. Zielfunktion in einer Variablen:<br />
2 A = ( x + 12)<br />
⋅ ( 15 − x)<br />
3<br />
4. Bestimmung des Extremums:<br />
M<strong>ax</strong>imaler Inhalt für x = 1.5 dm. Länge: 13.5 dm, Breite 9 dm<br />
e)<br />
Bewegung zweier Massenpunkte<br />
⎛− 3⎞<br />
Der 1. Punkt: startet zur Zeit t = 0 in A(7, 0), Geschwindigkeit vA = ⎜ ⎟<br />
⎝ 0 ⎠<br />
r<br />
⎛ 0 ⎞<br />
Der 2. Punkt startet zur Zeit t = 0 in B(0, 6), Geschwindigkeit vB = ⎜ ⎟<br />
⎝−<br />
4⎠<br />
r<br />
Zu welcher Zeit ist der Abstand der beiden Punkte minimal?<br />
1. Zielfunktion:<br />
Stelle die Grösse, die extremal werden soll, mit<br />
Hilfe geeigneter Variablen dar:<br />
Der Abstand ist genau dann minimal,<br />
wenn das Abstandsquadrat D minimal ist.<br />
D = x 2 + y 2<br />
2. Nebenbedingungen :<br />
x = 7 - 3t y = 6 - 4t<br />
3. Zielfunktion als <strong>Funktion</strong> einer einzigen<br />
Variablen<br />
D(t) = (7 - 3t) 2 + (6 - 4t) 2 = 25t 2 - 90t + 85<br />
4. Bestimmung des Extremums:<br />
b 90 9<br />
Das Abstandsquadrat wird minimal für t = − = = 50 5<br />
2a<br />
Das minimale Abstandsquadrat ergibt sich mit 3. zu D = 4. Der minimale Abstand ist also 2.<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
10
13. Ein Beispiel aus der Physik: Der schiefe Wurf<br />
r ⎛ vx<br />
⎞<br />
Ein Stein wird von einer um h erhöhten Plattform mit der Geschwindigkeit v = ⎜ ⎟ mit<br />
v<br />
2<strong>7.</strong>03.2013 quadrfkt_neu/ul<br />
⎝ y ⎠<br />
vx > 0 geworfen (der Luftwiderstand wird nicht berücksichtigt). Nach welcher Zeit erreicht er<br />
den höchsten Punkt und wie gross ist die Scheitelhöhe.<br />
Bewegungsgleichung für den schiefen Wurf ohne Luftwiderstand:<br />
1) x = v x⋅<br />
t<br />
1 2<br />
2) y = v ⋅t − gt + h h > 0<br />
y<br />
x<br />
aus 1) t = eingesetzt in 2)<br />
v<br />
x<br />
2 y<br />
y x x h<br />
2<br />
2vx<br />
vx<br />
2<br />
g v<br />
= − ⋅ + ⋅ + mit x > 0<br />
numerisches Beispiel:<br />
h = 8 m, vx = 20 m/s, vy = 15 m/s, g = 10 m/s 2<br />
1 2 3<br />
y = − 80 ⋅ x + 4 x + 8<br />
Der Stein erreicht den höchsten Punkt S in 30 m horizontaler Entfernung, wegen 1) nach 1.5 s.<br />
Die Scheitelhöhe beträgt 19.25 m, die erreichte Weite 69.2 ≈ 70 m.<br />
Im allgemeinen Fall mit h = 0, Anfangsgeschwindigkeit v0 und Abwurfwinkel α gilt:<br />
x(t) = v0⋅t⋅cos α (1)<br />
y(t) = v0⋅t⋅sin α - ½ gt 2 (2)<br />
(1) nach t aufgelöst<br />
0 cos<br />
x<br />
t =<br />
v α<br />
eingesetzt in (2)<br />
Gleichung der Bahnkurve (Wurfparabel):<br />
g<br />
2<br />
y = − ⋅ x + x ⋅ tanα<br />
(3)<br />
2 2<br />
2v<br />
cos α<br />
Wurfweite w in horizontaler Richtung:<br />
2<br />
v0<br />
sin( 2α<br />
)<br />
w =<br />
g<br />
zugehörige Wurfzeit T:<br />
v<br />
T =<br />
g<br />
2 0 sinα<br />
Scheitelhöhe h: h<br />
Bei gegebenem v0 wird<br />
v<br />
0<br />
= 0<br />
2 2<br />
= 0<br />
2<br />
w m<strong>ax</strong>imal für α = 45° w v<br />
g<br />
h m<strong>ax</strong>imal für α = 90° w v<br />
=<br />
g<br />
0<br />
2<br />
2<br />
T m<strong>ax</strong>imal für α = 90°<br />
v<br />
T =<br />
g<br />
2 0<br />
sin α T<br />
(y-Wert zur Zeit /2)<br />
2g<br />
11