ERGEBNISSE TECHNISCHE MECHANIK III-IV - Lehrstuhl für ...

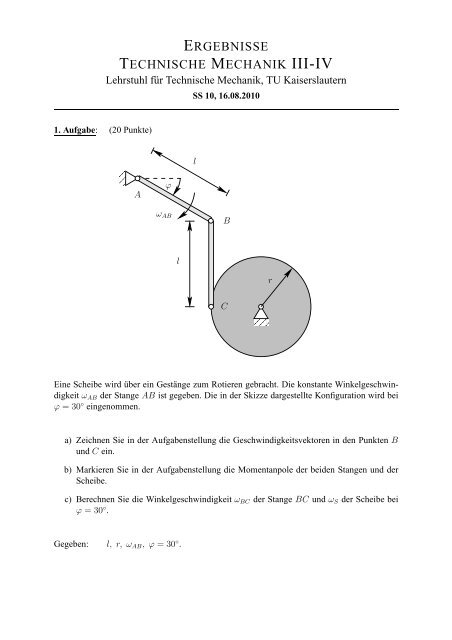
1. Aufgabe: (20 Punkte)
ERGEBNISSE
TECHNISCHE MECHANIK III-IV
Lehrstuhl für Technische Mechanik, TU Kaiserslautern
01
01
01
A
ϕ
ωAB
l
SS 10, 16.08.2010
l
B
C
r
00 11
Eine Scheibe wird über ein Gestänge zum Rotieren gebracht. Die konstante Winkelgeschwindigkeit
ωAB der Stange AB ist gegeben. Die in der Skizze dargestellte Konfiguration wird bei
ϕ = 30 ◦ eingenommen.
a) Zeichnen Sie in der Aufgabenstellung die Geschwindigkeitsvektoren in den Punkten B
und C ein.
b) Markieren Sie in der Aufgabenstellung die Momentanpole der beiden Stangen und der
Scheibe.
c) Berechnen Sie die Winkelgeschwindigkeit ωBC der Stange BC und ωS der Scheibe bei
ϕ = 30 ◦ .
Gegeben: l, r, ωAB, ϕ = 30 ◦ .

a)
b)
c)
MI
01
01
A
01
01
01
A
ϕ
ωAB
ϕ
ωAB
vB
.
vB
B
C
vC
.
vC
B
C
MIII
00 11
r
000 111
MII

2. Aufgabe: (20 Punkte)
Θ2
x
R2
m3
00 11
00 11
ϕ2
r2
Das dargestellte System besteht aus zwei Walzen (m1, r1; Θ2, R2, r2) und einer Masse m3, die
über Seile miteinander verbunden sind. Die Seile sind dehnstarr und masselos. Das System sei
zunächst in Ruhe und beginne sich unter einem konstanten Moment M0 zu bewegen.
a) Zeichnen Sie alle relevanten Freikörperbilder.
b) Bestimmen Sie die kinematischen Beziehungen zwischen den gegebenen Koordinaten.
c) Stellen Sie die dynamischen Gleichungen auf.
d) Berechnen Sie die Beschleunigung ¨x der Masse m3.
e) Bestimmen Sie die Seilkräfte.
f) Bestimmen Sie die Geschwindigkeit und die Strecke der Masse m3 zum Zeitpunkt t = 20.
Gegeben: r1 = 2 r, r2 = 3 r, R2 = 5 r; m1 = 2 m, m3 = 5 m;
Θ2 = 80 m r 2 ; M0 = 20 m g r; g.
r1
00 11
00 11
ϕ1
g
m1
M0

a) Freikörperbilder
x
III
ω2
S2
G3
b) x = 6
5 r ϕ1 = 3 r ϕ2, ϕ1 = 5
2 ϕ2
c)
A : M0 − S1 r1 = Θ1 ¨ϕ1
B : S1R2 − S2r2 = Θ2 ¨ϕ2
↑ : m3¨x = S2 − G3
v
S2
By
00 11
00 11
d) a = 1 M0 3
−
20 mr 10 g, mit M0 = 20mgr, a = 0, 7 g
e) S1 = 8 5
6 m g , S2 = 8 1
m g
2
II
f) v(t) = 0, 7 g t, v(20) = 14 g [m/s]
x(t) = 0, 7 g t2
, x(20) = 140 g [m]
2
G2
Bx
S1
S1
Ay
00 11
00 1101
G1
I
g
M0
ω1
Ax

3. Aufgabe: (20 Punkte)
ω
m
3
y
x
2 m
Mit dem Hammer aus der Skizze, der im Abstand h vom Hammerkopf in der Hand (gelenkiges
Lager) gehalten wird, wird mit der konstanten Winkelgeschindigkeit ω0 auf eine frei bewegliche
ruhende Kugel geschlagen.
ω0
a) Bestimmen Sie das Massenträgheitsmoment des Hammers bezogen auf dessen Schwerpunkt.
Betrachten Sie dazu den Hammerkopf als Punktmasse.
b) Für h = l
und e = 0.5 bestimmen Sie die Geschwindigkeit ¯
2 vK der Kugel und die
Winkelgeschwindigkeit ¯ω des Hammers unmittelbar nach dem Stoß. Betrachten Sie dazu
die Kugel als Punktmasse.
c) Bestimmen Sie den Abstand h der Hand vom Hammerkopf so, dass keine Stoßkraft in
der Hand entsteht.
Gegeben: m, l, ω0, e, h.
m
l
h

a) Θs = 1
4 ml2
b) ¯vK = − 21 13
ωl, ¯ω =
32 16 ω
c) h = 2
3 l

4. Aufgabe: (30 Punkte)
O ϕ m1
c
l l l
Ein homogener Balken (Länge 3l, Masse m1) ist in der statischen Ruhelage (ϕ = 0) im Punkt
O gelenkig gelagert und mit einer Feder c und einem Dämpfer d an den skizzierten Stellen
verbunden. Der Balken wird über eine massenlose Umlenkrolle durch die Masse m2 um den
Winkel ϕ = ϕ0 ausgelenkt. Das Seil wird zum Zeitpunkt t = 0 durchgeschnitten. Das gesamte
System befindet sich unter dem Einfluss der Erdbeschleunigung g.
Bestimmen Sie für kleine Auslenkungen ϕ:
a) Die Anfangsauslenkung ϕ0.
b) Die Differentialgleichung des frei schwingenden Balkens.
c) Das Lehrsche Dämpfungsmaß D und die gedämpfte Eigenfrequenz ωd.
d) Bestimmen Sie für folgende Fälle:
1. Schwach gedämpft: Die Lösung der Bewegungsgleichung mit Amplitude und
Phasengang.
2. Aperiodischer Grenzfall: Die Lösung der Bewegungsgleichung.
Zusatzaufgabe zu 2.: Nach welcher Zeit t klingt die Bewegung ϕ(t) auf 10 %
der Anfangsauslenkung ϕ0 ab? (Angabe ohne Nachkommommastelle ist ausreichend).
Gegeben: m1, m2, c, d, l, g.
d
m2
g

a) ϕ0 = 3m2g
cl
b) 3m1 ¨ϕ + 4d ˙ϕ + cϕ = 0
c)
D = 2d√3m1c , ωd =
3m1c
O
O
d1) ϕ(t) = Ce −δt cos(ωdt − β)
β = arctan( δ
ωd
), δ = 2d
3m1
d2) ϕ(t) = (ϕ0 + δϕ0t)e −δt
Zusatzaufgabe:
1
≤ (1 + δt)e−δt
10
t > 4
δ
ϕ0
ϕ
Ff
Ff
√ 3m1c − 4d 2
3m1
, C = ϕ0
cos(β)
Fd
m2g

5. Aufgabe: (40 Punkte)
y
α
l
x
β
Ein Doppelpendel besteht aus zwei massenlosen Stäben (Länge l) und einer Punktmasse (Masse
m) welche am Ende des zweiten Stabes befestigt ist. Das Doppelpendel sei im Koordinatenursprung
x − y gelagert und befinde sich unter dem Einfluss der Erdbeschleunigung g.
Bestimmen Sie in Abhängigkeit des Koordinatensystems x − y und der Winkel α und β:
a) Die Lagrangefunktion.
b) Die Bewegungsgleichungen.
c) Die linearen Bewegungsgleichungen für kleine Auslenkungen von α und β.
d) Die Eigenfrequenz für kleine Auslenkungen.
Gegeben: m, l, g.
Hinweis: cos(α ± β) = cosαcosβ ∓ sin α sin β
l
g
m

a) L = 1
2 ml2 ( ˙α 2 + ˙ β 2 + 2 ˙α ˙ β cos(α − β)) + mgl(cosα + cos(β))
b) ml 2 (¨α + ¨ βcos(α − β) − ˙ βsin(α − β)( ˙α − ˙ β)) + ml 2 ˙α ˙ β sin(α − β) + mgl sin(α) = 0
ml 2 ( ¨ β + ¨αcos(α − β) − ˙αsin(α − β)( ˙α − ˙ β)) − ml 2 ˙α ˙ β sin(α − β) + mgl sin(β)
c) l¨α + l ¨ β + gα = 0
l¨α + l ¨ β + gβ = 0
d) ω =
g
2l