Übungsblatt Nr

zusätzliches Übungsblatt Nr. 7 zur Thermodynamik WS 2010/2011
wird nicht in Übungsstunden behandelt; es soll dem Selbststudium dienen!
Thema: Funktion mehrerer Variablen, partielle Ableitungen. ⎯ Eigentlich wollen wir
"nur" das mathematische Werkzeug schärfen, das in der phänomenologischen
Thermodynamik benötigt wird. Dazu kann man von einer Formel ausgehen und dann daran
üben (Aufgaben 4,5). Alternativ kann man das mit einer Formel machen, die einen
anschaulicheren Hintergrund hat. So behandeln Aufgaben 1,2 die mikroskopische Struktur
und deren Verteilung, sind also in der statistischen Thermodynamik angesiedelt.
1. Aufgabe.
7´10 -20
V
6´10 -20
5´10 -20
4´10 -20
3´10 -20
2´10 -20
1´10 -20
-1.5 ´10 -11
-1´10 -11 -5´10 -12
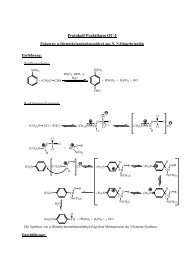
Wir betrachten ein H-Atom, welches
auf einer Si-Oberfläche gebunden ist.
Die Auslenkung aus der Ruhelage sei
a, die Feder-Kraftkonstante k. Die
potentielle Energie als Funktion der
Auslenkung ist
1
2
Bindungen betrachtet (oder dieselbe immer wieder neu) gewinnt man eine Häufigkeit oder
Wahrscheinlichkeit der Auslenkung (kB=R/NL ist die Boltzmann-Konstante)
2
1
⎛ 1/
2 k a ⎞
P(
a)
=
exp ⎜ −
⎟
2 π k T / k ⎝ k BT
B
⎠
2
V ( a)
= k a , was (für k=604.2 N m-1 ) oben links gezeigt ist. Wenn man sehr viele solcher
So sieht das für T=300 K aus und so für T= 600 K.
1.5 ´10 11
1.25 ´10 11
1´10 11
7.5 ´10 10
5´10 10
2.5 ´10 10
-1.5 ´10 -11
-1´10 -11
-5´10 -12
Pop
5´10 -12 1´10 -11
1.5 ´10 -11
a
Anstatt die Temperatur T zu verändern, könnte man auch die Kraftkonstante k der Bindung
verändern. Zum Beispiel entspricht das folgende Bild
7´10 -20
V
6´10 -20
5´10 -20
4´10 -20
3´10 -20
2´10 -20
1´10 -20
-1.5 ´10 -11
-1´10 -11
-5´10 -12
5´10 -12 1´10 -11
1.5 ´10 -11
a
5´10 -12 1´10 -11
1.5 ´10 -11
a
einer kleineren Kraftkonstante k=285.6 N m -1 .
Nun ist die Verteilung bei T=300 K
gegeben durch folgendes Bild:
also genauso breit, wie im obigen Fall der festeren Bindung erst
bei höherer Temperatur. Allgemein kann man auffassen P(a,k,T).
Man gewinnt zB Breite in a, wenn man entweder die Temperatur erhöht (erster Fall) oder die
Federkonstante erniedrigt (zweiter Fall).
Aufgabe: bilden Sie die partiellen Ableitungen
0
⎛
⎜
⎝
a
∂ P ⎞
⎟⎠
∂ T
a,
k
1.5 ´10 11
1.25 ´10 11
1´10 11
7.5 ´10 10
5´10 10
2.5 ´10 10
-1.5 ´10 -11
-1´10 -11
-5´10 -12
und
Pop
⎛
⎜
⎝
5´10 -12 1´10 -11
1.5 ´10 -11
a
∂ P ⎞
⎟⎠
∂ k
-1.5 ´10 -11
-1´10 -11 -5´10 -12
a,
T
1.5 ´10 11
1.25 ´10 11
1´10 11
7.5 ´10 10
5´10 10
2.5 ´10 10
Pop
5´10 -12 1´10 -11
1.5 ´10 -11
a

2. Aufgabe
Nun gibt es zwei Auslenkungen a und b. Für die potentielle
Energie V wird angenommen:
V ( a,
b)
=
1 2 1 2
k1a
+ k 2b
2 2
In den zwei nächsten Bildern ist angenommen:
k1 = 604.2 N m-1 , k2=285.6 N m-1 b
a
.
0
1´10 -19
7.5 ´10 -20
-1´10 -11
-1´10 -11
5´10 -20 V
2.5 ´10 -20
Aufgabe: Bilden Sie ( ∂ V / ∂ a ) b und ( V / ∂ b)
a
∂ !
Zeigen Sie, daß die Voraussetzungen des Satzes von Schwarz erfüllt sind!
Nun machen wir das etwas komplizierter: die beiden Federn werden "verkoppelt". Das
bedeutet, daß die potentielle Energie einen sog. "Kreuzterm" enthält:
V ( a,
b)
1
2
1
+
2
k12=150 N m-1 .
2
2
= k1a
+ k12
a b k 2b
. Im Folgenden sehen sie dies mit k1, k2 wie oben und
Nun folgen die beiden partiellen Ableitungen, links nach
a, und rechts nach b.
Wichtig: diese sind natürlich auch Funktionen von a,b !
die
0
-1´10 -11
-1´10 -11
1´10 -11
b 1´10 -11
b
0
1´10 -19
V
0
a
-1´10 -11
-1´10 -11
5´10 -20
0
-1´10 -11
-1´10 -11
1´10 -11
1´10 -11
1´10 -11
b 1´10 -11
b
0
1.5 ´10 -11
1´10 -11
5´10 -12
0
-5´10 -12
-1´10 -11
-1.5 ´10 -11
0
a
1´10 -11
1´10 -11
-1.5 ´10 -11
-1´10 -11
-5´10 -12 0 5´10 -12 1´10 -11
1.5 ´10 -11
1.5 ´10 -11
1´10 -11
5´10 -12
0
-5´10 -12
-1´10 -11
-1.5 ´10 -11
1.5 ´10 -11
-1.5 ´10 -11
-1.5 ´10 -11
-1´10 -11
-5´10 -12 0 5´10 -12 1´10 -11
1.5 ´10 -11
1´10 -11
5´10 -12
0
-5´10 -12
-1´10 -11
-1.5 ´10 -11
-1´10 -11
-5´10 -12 0 5´10 -12 1´10 -11
1.5 ´10 -11
1.5 ´10 -11
Aufgabe: (i) geben Sie
-1.5 ´10 -11
-1.5 ´10 -11
-1´10 -11
-5´10 -12 0 5´10 -12 1´10 -11
1.5 ´10 -11
entsprechenden Formeln an!
(ii) Zeigen Sie, daß die Voraussetzungen des Satzes von Schwarz erfüllt sind!
1´10 -11
5´10 -12
0
-5´10 -12
-1´10 -11

3. Aufgabe:
Zurück in die phänomenologische Thermodynamik! Dort werden Beziehungen von u, s,
v, T, P, n etc behandelt, die als solche meistens nicht anschaulich einsichtig sind. Sie
werden aus mikroskopischen Betrachtungen wie oben zwar prinzipiell gewonnen, doch
einfacher kann man diese Beziehungen messen.
Stellen Sie sich also vor, man könnte an einem abgeschlossenen System S und V
(diesmal molare Größen, also n=1) verändern und U messen. Die vielen Datenpunkte
werden irgendwie versuchsweise in eine Formel gebracht, und hier ist sie:
3
( β S V )
U ( S,
V)
= Aln
+
wobei im konkreten Fall natürlich A und β einen Wert besitzen.
⎛ ∂ U ⎞
⎛ ∂ U ⎞
Bestimmen Sie die partiellen Ableitungen ⎜ ⎟⎠ als f(S,V) und ebenso ⎜ ⎟⎠
⎝ ∂ S V
⎝ ∂ V
Zeigen Sie, daß die Voraussetzungen des Satzes von Schwarz erfüllt sind!
4. Aufgabe:
(Letzteres heißt, es gibt eine Funktion U(S,V) – was wir aber schon wissen, denn
da kommen wir ja gerade her! ).
Wir stellen uns vor, es existieren Meßdaten (ΔU/ΔS)V für ganz viele Zustände {Si, Vi }
(1., 2., ....i. ...N usw Meßpunkt, typisch N=1000 Punkte) und ebenso (ΔU/ΔV)S. Um U
zu finden, muß man diese Meßdaten zunächst in eine empirische Formel bringen (sog.
Datenanpassung oder "Data fitting").
(a) Es sei zunächst versucht:
( ∂ U / ∂ S)
V
1
= B 3 und ( ∂ U / ∂ V)
S =
S + V
2V
B 2 .
S + V
1 2V
Ist B dS + B dV
3
2 ein vollständiges Differential, lohnt es sich also, durch
S + V S + V
Integration U zu ermitteln?
(b) Der Experimentator sagt Ihnen, man könnte die Daten auch ganz gut mit
( ∂ U / ∂ S)
V
1
= B 2 und ( ∂ U / ∂ V)
S =
S + V
2V
B 2 fitten.
S + V
1 2V
Ist B dS + B dV
2
2 ein vollständiges Differential, lohnt es sich also, durch
S + V S + V
Integration U zu ermitteln?
(c) Wo ein vollständiges Differential vorliegt (Fall a oder b):
Nehmen Sie an, bei {S1,V1}, also dem ersten Meßpunkt, sei das zugehörige U1 bekannt.
Was ist dann die Formel für U als f(S,V) ?
S
!