∫

2.1 Grundwissen 2.1.3. Thermodynamik des Supraleiters 23
Dies kann in Figur 2.12 eingezeichnet werden, und zwar im unteren Teilbild als
Extrapolation der Parabel des Meissnerzustandes bis zum Schnittpunkt mit der
Geraden F=F NL , und im oberen Teilbild durch die skizzierte Konstruktion mit
Flächengleichheit (A 1 =A 2 ).
Die Angabe von B cth folgt aus rein praktischen Gründen, z.B. wenn die
Magnetisierungsarbeit (=Fläche unter der Magnetisierungskurve) bestimmt werden
soll ist es nützlich, das Integral eines fiktiven SL 1.Art zu verwenden.
Somit gilt formell auch für den Supraleiter 2. Art:
2
Bcth
F
NL
− FSL
(0) = V
2µ
(2.2)
Bisher wurde nur der Unterschied der Helmholtzschen Freien Energie mit und ohne
Feld betrachtet. Es galt:
F
SL
( B ) − F
a
SL
Der Ausdruck rechts vom Gleichheitszeichen beschreibt hierbei die magnetische
Dipolenergie im Feld B a .
Um die Freie Energie des Normalleiters zu bestimmen, verwendet man beim
SL 1. Art: B a =B c =B cth bzw. beim SL 2. Art: B a =B cth . Somit gilt für beide:
2
Bcth
F
NL
− FSL
(0) = V
2µ
0
Diese Angabe ist für den SL 1. Art wirklich gültig und für den SL 2. Art per
Definition von B cth erfüllt.
Die Freie Energie im Nullfeld hängt ab von der inneren Energie, der Temperatur und
der Entropie, weshalb nun auf die Entropie des Supraleiters eingegangen wird.
0
(0) = V
B a
∫
0
MdB
/
a
2.1.3.2 Die Entropie des Supraleiters
Ist kein Feld vorhanden, so gilt sowohl für die Freie Energie des Supraleiters als
auch für die Freie Energie des Normalleiters:
F=U-TS
wobei U die innere Energie, T die Temperatur und S die Entropie ist.
Das Differential ist dann gegeben mit:
dF=dU-TdS-SdT
Nach dem 1. Hauptsatz der Thermodynamik gilt für dU:
dU=δQ-dW
Dabei beschreibt δQ die zugeführte Wärme und dW die vom System geleistete
mechanische Arbeit.
In der Regel leistet der Supraleiter keine mechanische Arbeit, weshalb dW = 0
angenommen wird. Somit gilt für die innere Energie:
dU=δQ

2.1 Grundwissen 2.1.3. Thermodynamik des Supraleiters 24
Die zugeführte Wärme δQ kann man über die Entropie ausdrücken (2. Hauptsatz der
Thermodynamik):
δ Qreversibel
dS = ⇒ δ Q = TdS ⇒ dU = TdS
T
Somit läßt sich die Freie Energie angeben als:
dF=TdS-TdS-SdT=-SdT
bzw.
S
= −
dF
dT
Dies gilt im Falle des Nullfeldes sowohl für den Supraleiter als auch für den
Normalleiter. Es muß nur die entsprechende Freie Energie (F NL bzw. F SL ) eingesetzt
werden.
Es soll dies nun auf die Entropiedifferenz zwischen NL und SL angewendet werden.
Es gilt:
S
NL
−
S
SL
d
( B = 0) = − ( FNL
− FSL
(0))
dT
F NL -F SL (0) wurde bereits in Formel 2.2 definiert. Dies eingesetzt ergibt:
S
NL
−
S
0) = −
2
SL
(
cth
2µ
0
dT
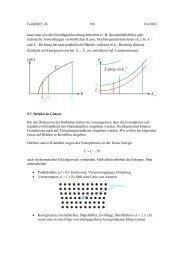
Der Verlauf von B cth ist bekannt. Nun kann qualitativ daraus der Ausdruck für die
Entropiedifferenz bestimmt werden. Dies ist in Figur 2.13 gezeigt. Teilbild a) zeigt
den gewohnten Verlauf des thermodynamischen kritischen Feldes in Abhängigkeit
von der Temperatur. Wie später gezeigt wird, mündet die Tangente an die Kurve bei
2
T=0 waagerecht ein. In Bild b) ist der Verlauf von B cth angegeben. Der lineare
2
Verlauf von B cth bei T c bedingt nun einen parabelförmigen Anstieg von B cth
. Nach
2
einem Wendepunkt geht B cth für T → 0 wieder in Sättigung über. In Figur c) ist
2
schließlich die Ableitung von B cth
nach der Temperatur mit umgekehrten Vorzei-chen
gegeben. Für den parabelförmigen Verlauf von b) bei T c erhält man bei Ableitung
einen linearen Anstieg. Die Kurve in c) durchläuft dann ein Maximum beim
Wendepunkt von b).
Aus dieser qualitativen Betrachtungsweise kann gefolgert werden:
a) T=0: Nach dem Satz von Nernst gilt, daß die Entropie S→ 0 geht, wenn T→ 0
geht. (3. Hauptsatz der Thermodynamik; Bedingung: es muß sich ein
Gleichgewicht einstellen). Damit ist die Entropie des Normalleiters und die
des Supraleiters Null. Es gilt also: S NL -S SL (0)=0. Die Kurve (Bild c)) muß
also für T=0 in den Nullpunkt laufen. Somit ergibt sich die bereits erwähnte
waagrechte Tangente sowohl in Bild b) als auch in Bild a) bei T=0.
V
d
B

2.1 Grundwissen 2.1.3. Thermodynamik des Supraleiters 25
Fig. 2.13: qualitative Ableitung des Verlaufes der Entropiedifferenz S NL -S SL
b) 0

2.1 Grundwissen 2.1.3. Thermodynamik des Supraleiters 26
2.1.3.3 Die Wärmekapazität eines Supraleiters:
Sie ist definiert als:
dQ
C = = T
dT
dS
dT
Im Gegensatz zu Gasen, wo zwischen einer spezifische Wärmekapazität bei
konstantem Druck c p bzw. konstantem Volumen c v unterschieden wird, wird hier
aufgrund der zu vernachlässigenden Volumenänderung nur eine spezifische
Wärmekapazität angegeben. (Die Wärmeausdehnung ist vernachlässigbar, weshalb
keine mechanische Arbeit geleistet wird ⇒ c p =c v. )
Es soll nun die Differenz der Wärmekapazität zwischen SL und NL angegeben
werden. Es gilt:
d
CSL
(0) − C
NL
= T ( S
SL(0)
− S
NL
)
dT
Dies wird wieder graphisch veranschaulicht (s. Fig. 2.14). (Beachte: Im Gegensatz zu
Fig. 2.13 wurde S SL -S NL aufgetragen.)
Fig. 2.14: Differenz der Wärmekapazität zwischen SL und NL graphisch abgeleitet.
In Bild a) ist die Entropiedifferenz von Fig. 2.13 gegeben. Teilbild b) zeigt qualitativ
die Ableitung der Kurve von a). Das Minimum in a) ist in b) als Nulldurchgang
erkennbar. Bei T=0 bzw. T=T c ist in b) die Kurve maximal, da in a) an diesen
Punkten die maximale Steigung vorliegt. Die Differenz der Wärmekapazität ist durch
Multiplikation von b) mit der Temperaturgeraden gegeben (s. Bild c)). Da die
Temperaturgerade durch den Ursprung geht, folgt aus der Multiplikation, daß bei
T=0 ∆C=0 ist. Außerdem ist ∆C für T>T c Null.

2.1 Grundwissen 2.1.3. Thermodynamik des Supraleiters 27
Die Wärmekapazität des Normalleiters ist aus der Festkörperphysik bekannt. Sie
setzt sich bei Metallen aus dem elektronischen und dem phononischen Anteil
zusammen. Für Temperaturen weit unterhalb der Debyetemperatur gilt:
C NL =γT+A T ³
wobei γT den elektronischen und AT³ den phononischen Anteil repräsentiert. Meist
bezeichnet man γ auch als den Sommerfeldparameter.
Zieht man von C NL den phononischen Anteil ab, so erhält man den rein
elektronischen Anteil, wie er in Figur 2.15 gezeigt ist (punktiert).
Fig. 2.15: Wärmekapazität eines SLs bzw. NLs
Nach 2.14 ist der Verlauf von ∆C=C NL -C SL bekannt. Mit dem Verlauf der
Wärmekapazität des NL kann daraus die Wärmekapazität des SL (s. Fig. 2.15)
angegeben werden. Sie liegt zunächst unterhalb der des NL. Mit zunehmender
Temperatur schneidet sie jedoch die Gerade. Wird die kritische Temperatur erreicht,
kommt es zu einem Sprung in der Wärmekapazität des SL.
Immer wenn ein Sprung in der Wärmekapazität zu verzeichnen ist, und wenn keine
latente Wärme auftritt, spricht man von einem Phasenübergang 2. Ordnung. Dieser
Sprung ist direkt meßbar, wie das Beispiel in Fig. 2.16 zeigt. Hier ist die spezifische
Wärmekapazität von Al sowohl im NL als auch im SL Zustand gezeigt. Den NL
Zustand für tiefe Temperaturen erzwingt man dabei durch ein äußeres Magnetfeld,
Fig. 2.16: Verlauf der spezifischen Wärmekapazität von Al im NL und SL Zustand. Deutlich ist der
Sprung in der spezifischen Wärmekapazität zu erkennen.

2.1 Grundwissen 2.1.3. Thermodynamik des Supraleiters 28
das größer ist als das kritische Feld. Im Normalleiter hat das Magnetfeld keinen
Einfluß auf die Wärmekapazität. Da die Sprungtemperatur in Aluminium sehr tief
liegt (1.2 K), ist hier der phononische Anteil zur spezifischen Wärmekapazität sehr
gering.
Nach der BCS-Theorie gilt für den Sprung der spezifischen Wärmekapazität bei T c :
wobei γT c =C NL (T c ) ist.
∆C(
T
γ T
c
c
)
= 1,43
Tabelle 2.1 zeigt zum Vergleich experimentell bestimmte Werte. Für viele Metalle
ist die Übereinstimmung recht gut. Einige zeigen aber Abweichungen. Dies sind die
sog. “stark koppelnden” Supraleiter.
Tab. 2.1: Sprungverhältnis der Wärmekapazität für unterschiedliche Elemente.
Bei Hochtemperatursupraleitern ist ebenfalls ein Sprung in der Wärmekapazität
vorhanden. Aufgrund der höheren Temperaturen trägt in diesem Fall der
phononische Anteil stärker bei. Das Debyesche T³-Gesetz ist nicht mehr gültig. Figur
2.17 zeigt einen Verlauf der spezifischen Wärmekapazität für zwei HTS-Materialien.
Man erkennt einen kleinen Sprung der spezifischen Wärmekapazität bei T c .
Schätzt man den rein elektronischen Anteil ab, so gilt für das Verhältnis:
∆C(
T
γ T
c
c
)
= 1−
2
Die BCS – Theorie ist also wieder in etwa erfüllt.

2.1 Grundwissen 2.1.3. Thermodynamik des Supraleiters 29
Fig.: 2.17:
Verlauf der spezifischen Wärmekapazität für einen HTS. Auch hier ist ein Sprung in der
spezifischen Wärmekapazität des SL zu erkennen. Allerdings wird die Messung durch
den phononischen Anteil stark beeinträchtigt.
Betrachtet man den Verlauf der spezifischen Wärmekapazität von Fig. 2.16
nochmals, so erkennt man, daß für T nicht zu weit unterhalb von T c die spezifische
Wärmekapazität des SL höher als die des NL ist. Dies ist typisch für einen
Phasenübergang 2. Ordnung. Die Kondensationswärme verteilt sich über einen
ganzen Bereich. Dies bedeutet, daß ab T c innerhalb eines Temperaturintervalls eine
allmähliche Kondensation der Elektronen zu Paaren stattfindet. Die Ordnung stellt
sich erst allmählich ein.
Anmerkung:
Vergleiche dazu das Schmelzen von Eis (Phasenübergang 1. Ordnung). Hier
kommt es bei einer bestimmten Temperatur zu einem Übergang von der festen in
die flüssige Phase. Erst wenn die gesamte Masse flüssig ist, erhöht sich die
Temperatur weiter.
Für tiefere Temperaturen T→ 0 wird die spezifische Wärmekapazität des SL sehr
klein. Die Elektronen sind fast alle gebunden. Man spricht davon, daß sie im
Grundzustand „ausgefroren“ (=geordnet) sind. Der SL hat keine Entropie mehr und
kann deshalb keine Wärme mehr aufnehmen. Hierzu sollen genaue Messungen von
metallischen Supraleitern (=Tieftemperatur SL) und oxidische SL (=Hochtemperatursupraleitern)
betrachtet werden.

2.1 Grundwissen 2.1.3. Thermodynamik des Supraleiters 30
a) metallische Supraleiter:
Figur 2.18 zeigt den Verlauf der spezifischen Wärmekapazität für die
metallischen Supraleiter Vanadium und Zinn. Aufgetragen ist die spezifische
Wärmekapazität des SL normiert auf die Wärmekapazität des NL als Funktion
von T c /T. Man erkennt, daß ein exponentielles Ausfrieren der Elektronen vorliegt.
Der Verlauf läßt sich durch eine logarithmische Gerade anpassen.
Fig. 2.18:
spezifischen Wärmekapazität im SL ohne Feld als Funktion von T c /T (Buckel)
Die logarithmische Gerade läßt sich darstellen als:
C ∝ e
∆
−
k B T
Bei dieser Messung war ∆≈1,5 k b T c . Die BCS Theorie liefert einen Wert von 1.73.
Diese Aktivierungsenergie ∆, die wir später als Energielücke (energy gap)
identifizieren, ist also in der Größenordnung der thermischen Energie bei T c .
Ein solches exponentielles Ausfrieren läßt sich nur bei metallischen SL finden.
b) Oxidische Supraleiter (HTS):
Diese zeigen ein Potenzgesetz beim Ausfrieren:
α
C SL
∝ T
α :1- 2
Je sauberer der SL, d.h. je weniger Defekte der Einkristall hat, desto mehr nähert
sich α dem Wert 1 an. Dieses Verhalten weist auf eine anisotrope Energielücke
hin. Sie ist richtungsabhängig im k-Raum. Diese Richtungsabhängigkeit im HTS
entspricht einem d 2 2 − Orbital.
x −y
Aus diesem Grund spricht man bei den HTS auch von d-Wellen SL. Fig. 2.19
zeigt dies schematisch.
Fig. 2.19: Richtungsabhängigkeit der Energielücke im k-Raum.

2.1 Grundwissen 2.1.3. Thermodynamik des Supraleiters 31
Entlang der Knotenlinien gilt, daß die Energielücke = 0 ist. Dies bedeutet, daß
sich dort nicht kondensierende Elektronen aufhalten können. Aus diesem Grund
erhält man eine schwächere (Potenzgesetz statt exponentielles Verhalten)
Temperaturabhängigkeit der Wärmekapazität. Die Elektronen frieren langsamer
aus.
Bemerkung:
Generell gilt, daß je tiefer die Temperatur ist, desto besser sind die supraleitenden
Eigenschaften. Dies gilt nicht nur für ein äußeres Magnetfeld, sondern wie in
Fig. 2.20 gezeigt auch für den Strom. Es wird dabei analog zum kritischen B-Feld
eine sog. kritische Stromdichte j c definiert.
Fig. 2.20: Abhängigkeit der kritischen Stromdichte bzw. des kritischen Magnetfeldes von der
Temperatur.
Die Wirkung des Stromes liegt dabei in seinem magnetischen Selbstfeld, welches
den gleichen Einfluß wie ein äußeres Magnetfeld auf den Supraleiter hat.
Damit erhält man ein einfaches Bild für die Elektronen im SL. Nebeneinander gibt es
in allen SL zwei Sorten von Elektronen, nämlich
a) kondensierte, supraleitende Elektronen ohne Widerstand und ohne Entropie, die
sog. Supraflüssigkeit.
b) unkondensierte, normalleitende Elektronen mit Entropie und mit Widerstand, die
sog. Normalflüssigkeit. Da beide Sorten von Elektronen im Metall parallel
geschaltet sind, werden die normalleitenden durch die supraleitenden Elektronen
kurzgeschlossen. Nur bei hohen Frequenzen, bei denen die
Beschleunigungskräfte für die supraleitenden Elektronen merklich werden, ist
der Kurzschluß nicht mehr vollständig, und es läßt sich ein Widerstand messen.
Dieses sog. 2-Flüssigkeits-Modell wurde ca. 1930 von Gorter und Kasimir
vorgeschlagen. Es ist auch heute noch nützlich, z.B. für die Berechnung des
Widerstandes von HTS für Mikrowellenfilter. Die BCS-Theorie hat auch gezeigt,
daß es tatsächlich 2 Sorten von Elektronen im Supraleiter gibt, die Paare und die
einzelnen Elektronen. Doch sind diese nicht so unabhängig voneinander, wie dies
von Gorter und Kasimir angenommen wurde. Wir wollen uns zunächst mit der
„Supraflüssigkeit“, also den Paaren, näher beschäftigen.

2.2 Supraflüssigkeit 2.2.1. Einführung 32
2.2 Supraflüssigkeit
2.2.1 Einführung
2.2.1.1. Elektronenpaare
1935 erklärte F. London, daß das Kondensat nicht mit klassischer Physik
beschreibbar ist, sondern er postulierte eine quantenmechansiche Phänomenologie
für die SL. Darin bezeichnete er das Kondensat als eine makroskopische
Wellenfunktion mit einer Phase. Dies versteht man besser, wenn man im Vorgriff auf
die BCS-Theorie die Eigenschaften von Elektronenpaaren betrachtet.
Betrachten wir zunächst ein einzelnes Elektronenpaar mit Elektronen am Ort r 1 bzw.
r 2 . Um einen gebundenen Zustand zu erlangen, wird eine anziehende
Wechselwirkung benötigt. Diese Wechselwirkung ist nur vom Abstand zwischen den
Elektronen (r 1 -r 2 ) abhängig. Zusätzlich fordern wir noch, daß die Spins
antisymmetrisch sein sollen. Dies hat den Vorteil, daß wir eine symmetrische (und
dadurch einfachere) Ortswellenfunktion erhalten.
Die daraus resultierende 2-Teilchenwellenfunktion läßt sich angeben mit:
Y(r 1 ,r 2 ) = y 1 (r 1 )y 2 (r 2 )
Dies ist vergleichbar mit dem 2-Körper Problem der klassischen Mechanik.
Entsprechend zu der dort eingeführten Aufteilung in eine Schwerpunktskoordinate r s
und eine Relativkoordinate r r ,
r r
r r r
1
+
2
r r r
1
,
2
→
s
= ;
r
=
1
−
2
2
kann man hier die Wellenfunktion separieren: (s. z.B. Schwabl QM: Kap. 6.4)
Y(r 1 ,r 2 ) = F(r s )y(r r )
wobei
F(r s ) die Schwerpunkt-Wellenfunktion und
y(r r ) die Relativ-Wellenfunktion ist.
Als Beispiel sei hier das Wasserstoffatom angeführt:
Befindet man sich am Ort des Protons (≈Schwerpunkt), so entspricht die relative
Wellenfunktion y(r r ) dem Orbital des Elektrons.
Die Schwerpunktsbewegung eines freien H-Atomes ist gegeben durch:
r Φ s ) = e
r r
ik s s
(
iΘ
( r
s
) = e
Befindet sich das H-Atom in Ruhe, so ist k s =0. Dann bleibt nur noch:
Φ
Θ stellt dabei einen beliebigen Phasenwinkel dar. Daher genügt es in der
Quantenmechanik nur die Relativkoordinaten zu betrachten.

2.2 Supraflüssigkeit 2.2.1. Einführung 33
Der Supraleiter enthält nun viele solche Paare. Da sie jeweils den Spin 0 besitzen,
müssen wir uns fragen, ob sie als Bosonen angesehen werden können. Ein typisches
Bosegas ist Heluium 4. Im Kern des 4 He sind 4 Fermionen mit Spin 0 gebunden. Die
Elektronen bilden eine abgeschlossene Edelgasschale, haben also ebenfalls Spin 0.
Der Durchmesser des He-Atoms beträgt ca. 0,05 nm, der mittlere Abstand im
flüssigen Helium bei Atmosphärendruck 0,36 nm. Die Nachbarn sind also genügend
weit weg, so daß die innere Struktur des He-Atoms keine Rolle spielt und das ganze
6-Teilchen-System nach außen als Boson wirkt.
Anders ist es aber für die Paare im Supraleiter. Hier ergibt sich folgende
Abschätzung:
Da die Elektronen relativ zueinander lokalisiert sind, entspricht der
Bahndurchmesser ihrer Ortsunschärfe ∆x. Nach der Unschärferelation
∆x∆p ≈ h
ist ∆x ≈ h /∆p. Da der Impuls mindestens gleich seiner Unschärfe ist, benötigt man
zur Lokalisierung die Mindestenergie:
Diese nennt man auch die Lokalisierungsenergie. Sie ist z.B. im H-Atom dafür
verantwortlich, daß das Elektron nicht in den Kern stürzen und dadurch potentielle
Energie gewinnen kann.
Hier steht zur Lokalisierung nur die geringe Paarbindungsenergie
∆ SL ≈k B T c
zu Verfügung. Dies ergibt die Abschätzung:
bzw.:
2
( ∆p)
2
E p
= ≈
kin
2m
2 m
∆p
≈ 2mk T B c
∆x
≈
2 mk T B
Setzt man z.B. eine kritische Temperatur von 10 K ein ergibt sich ein Bahnradius
von ca. 40 nm. Im allgemeinen bezeichnet man den Druchmesser der Paare als
Kohärenzlänge x. In realen SL gilt als Größenordnung für diesen Durchmesser
- Metallische SL: 10 nm
- oxidische SL: 1,5 nm
h
c
Das in der Abschätzung erhaltenen Ergebnis ist also innerhalb der gleichen
Größenordnung wie die Meßwerte für metallische SL.

2.2 Supraflüssigkeit 2.2.1. Einführung 34
Die Relativ-Wellenfunktion (=Orbital) eines Paars nach der BCS-Theorie ist in Figur
2.21 dargestellt.
Fig. 2.21: Relativ-Wellenfunktion eines Paares
In Metallen ist die Elektronenkonzentration in etwa:
N 23 −3
≈ 10 cm
V
Dies entspricht einem mittleren Abstand von 0,2 nm. Innerhalb eines
Kohärenzvolumens ∼x³ (d.h. das Volumen eines Paares) ergeben sich somit
10 5 Paare in metallischen SL bzw.
10 3 Paare in oxidischen SL.
Es liegt also eine starke gegenseitige Durchdringung der Paare vor. Die Paare wirken
daher für ihre Nachbarpaare nicht als Bosonen, sondern ganz wesentlich als
Fermionen, die sich auf der 0,2 nm Skala gegenseitig aus dem Wege gehen, wie im
Normalleiter. Torzdem können sie auf der 10 nm-Skala Bose-ähnliches Verhalten
zeigen, indem sie alle dieselbe Schwerpunkts-Wellenfunktion einnehmen. Dieser
Zustand wird durch das Pauliprinzip sogar begünstigt. Nehmen wir an (s. Fig. 2.22),
alle Paare bis auf eines (gestichelt) seien im selben Zustand der
Schwerpunktsbewegung, hätten also dieselbe Geschwindigkeit. Dann kreuzt das
einzelne Paar die Orte aller anderen, muß also in Zustände mit höherer kinetischer
Energie ausweichen, um dem Pauliprinzip zu genügen („Pauli-Abstoßung“). Es ist
also energetisch günstiger, wenn sich alle Paare gleich schnell bewegen, also alle
dieselbe Schwerpunkts-Wellenfunktion haben. Dies ist tatsächlich der Grundzustand
nach der BCS-Theorie oder die „makroskopische Wellenfunktion nach F. London“.
Fig. 2.22:
Schematische Darstellung der Schwerpunktsbewegung benachbarter Paare. Ein
entgegengesetzt laufendes Paar müßte, um nicht den gleichen Zustand wie ein anderes
Paar einzunehmen (Pauliprinzip) auf etwas höhere Energien ausweichen.

2.2 Supraflüssigkeit 2.2.1. Einführung 35
Die Bewegung aller Paare ist also gleich, d.h. quantenmechansich müssen alle die
gleiche Schwerpunktsbewegung haben. Dies wiederum bedeutet, daß sie alle die
gleiche Wellenfunktion und den selben Phasenfaktor
r
r r
Φ
ik s s
s
) = e
(
Θ
aufweisen. Selbst in Ruhe (k s =0 – d.h. kein Stromfluß) muß trotzdem die gleiche
Phase vorliegen.
i
Φ( r ) = e
s
Aus diesem Grund ist es möglich von einer makroskopischen Wellenfunktion zu
sprechen. Diese läßt sich als kohärenter Zustand darstellen.