E - Fachgebiet Hochspannungstechnik

Das System
der
Maxwellschen
Gleichungen
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 1

Die Maxwellschen Gleichungen in Integralform
Das vollständige System der Maxwellschen Gleichungen (Integralform)
Die beiden ersten Maxwellschen Gleichungen treffen Aussagen über die
Wirbel des magnetischen und des elektrischen Feldes.
1. Maxwellsche Gleichung (1. Hauptgleichung)
⎛ ∂D
⎞
∫Hds = ∫⎜J + ⎟dA
"Verallgemeinertes Durchflutungsgesetz"
∂t
L
A⎝
⎠
"Ein elektrischer Strom (Durchflutung) verursacht ein magnetisches Wirbelfeld."
ETIT II_13
ETIT II_20
2. Maxwellsche Gleichung (2. Hauptgleichung)
d
∫Eds
=− d
dt
∫B A "Induktionsgesetz"
L
A
ETIT II_17
"Ein zeitlich veränderlicher magnetischer Fluss induziert ein elektrisches Wirbelfeld."
Bei Abwesenheit zeitlich veränderlicher magnetischer Felder: ∫ E
d s
= 0
ETIT II_02
ETIT II_17
L
"Das elektrostatische Feld ist wirbelfrei."
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 2

Die Maxwellschen Gleichungen in Integralform
Die dritte und die vierte Maxwellschen Gleichung treffen Aussagen über die
Quellen des magnetischen und des elektrischen Feldes.
3. Maxwellsche Gleichung (1. Nebenbedingung)
∫ B
d A = 0 "Kontinuitätsgleichung für die magnetische Flussdichte"
A
"Das magnetische Feld ist quellenfrei."
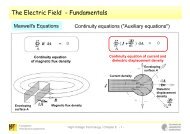
4. Maxwellsche Gleichung (2. Nebenbedingung)
⎛
∂D
⎞
∫ ⎜J
+ ⎟dA=
0 "Kontinuitätsgleichung für die elektrische Stromdichte"
∂t
A ⎝ ⎠
"Das elektrische Strömungsfeld ist quellenfrei."
∂D
Umformung: ∫
d A =− d = i()
t
∂t
∫
J A
A
A
"Gaußscher Satz der Elektrostatik"
und Integration: ∫DdA
= ∫i()
t dt = Q
auch: "Satz vom Hüllenfluss"
A
ETIT II_16
"Die Quellen des elektrostatischen Feldes sind die elektrischen Ladungen."
ETIT II_10
(in vereinfachter Form
als 1. Kirchhoffscher Satz)
ETIT II_03
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 3

Die Maxwellschen Gleichungen in Integralform
Die drei Materialgleichungen stellen Beziehungen zwischen den Feldgrößen
her und beschreiben deren von den Eigenschaften des Materials abhängigen
Auswirkungen.
D
= ε E
Elektrische Verschiebungsdichte
Permittivität
Elektrische Feldstärke
J
= γ E
Elektrische Stromdichte
Elektrische Leitfähigkeit (Konduktivität)
Elektrische Feldstärke
B
=
µ H
Magnetische Flussdichte
Permeabilität
Magnetische Feldstärke
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 4

Die Maxwellschen Gleichungen in Integralform
1. Maxwellsche Gleichung 2. Maxwellsche Gleichung
Darstellung aus
Küchler: Hochspannungstechnik
Springer, Berlin, 1996
ISBN 3-540-62070-2
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 5

Die Maxwellschen Gleichungen in Integralform
3. Maxwellsche Gleichung
4. Maxwellsche Gleichung
Darstellung aus
Küchler: Hochspannungstechnik
Springer, Berlin, 1996
ISBN 3-540-62070-2
∫∫
A
∂D
d A =− d = i()
t
∂t
∫∫
J A
A
DdA= i()
t dt = Q
∫∫
A
∫
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 6

Die Maxwellschen Gleichungen in Integralform
Die 3 Materialgleichungen
γ
Darstellung nach
Küchler: Hochspannungstechnik
Springer, Berlin, 1996
ISBN 3-540-62070-2
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 7

Die Maxwellschen Gleichungen in Integralform
Verknüpfung elektrischer und magnetischer Felder
∫
L
⎛ ∂D
⎞
Hds = ∫⎜J + ⎟dA
∂t
A⎝
⎠
B
=
µ H
J
= γ E
D
= ε E
d
− ∫BdA
=
dt
A
∫
L
Eds
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 8

Die Maxwellschen Gleichungen in Integralform
Maxwellsche Gleichungen bei harmonischer Zeitabhängigkeit:
Zweckmäßigerweise Übergang zur komplexen Darstellung
Für die vom Ort (Aufpunkt P) und der Zeit t abhängigen Feldgrößen schreibt man
E( Pt , ) = Re
( ) j t
H( Pt , ) = Re ( ) j t
usw.
{ E Pe ω
}
{ H Pe ω
}
Darin sind die komplexen Größen E ( P)
, H
( P)
nur vom Ort abhängig.
Phasoren
Die Phasoren können grundsätzlich entweder als komplexe Effektivwerte oder
als komplexe Amplituden aufgefasst werden.
In der Feldtheorie üblich komplexe Amplituden
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 9

Die Maxwellschen Gleichungen in Integralform
1. Maxwellsche Gleichung bei harmonischer Zeitabhängigkeit:
∫
L
⎛ ∂D
⎞
Hds = ∫⎜J + ⎟dA
∂t
A⎝
⎠
Hds = J + j D dA= + j EdA
( ω ) ( γ ωε)
∫ ∫ ∫
L A A
2. Maxwellsche Gleichung bei harmonischer Zeitabhängigkeit:
∫
L
Eds
d
=−
dt
∫
A
BdA
Eds =− jω BdA=−jω µ HdA
∫
∫ ∫
L A A
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 10

Die Maxwellschen Gleichungen in differentieller Form
Im Allgemeinen setzt sich eine Vektorgleichung aus drei skalaren Gleichungen
zusammen.
⎛ ∂D
⎞
Zum Bsp. erhält man für die 1. Maxwellsche Gleichung ∫Hds = ∫⎜J + ⎟dA
∂t
L
A⎝
⎠
drei skalare Gleichungen, wenn man für das Flächenelement dA
nacheinander setzt:
Fall 1:
Fall 2:
Fall 3:
∆ A= ex∆ Ax
= ex∆ ∆
y z
∆ A= ey∆ Ay
= ey∆ ∆
z x
∆ A= ez∆ Az
= ez∆ ∆
x y
x
z
y
Im Folgenden vereinfachte Schreibweise für Gesamtstromdichte:
G
∂D
= J + ∂ t
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 11

Die Maxwellschen Gleichungen in differentieller Form
Fall 1:
∆ A= ex∆ Ax
= ex∆ ∆
y z
Für infinitesimal kleine Längenelemente
∫ H
d s
= G A = Ge
∆x, ∆y, ∆z erhält man:
∆ ∆ = ∆y∆z
Für den Umlauf der linken Seite:
3
d x y z Gx
2 3 4 1
∫ = ∫ + ∫ + ∫ + ∫
L
1 2 3 4
4
= ( x, yz , +∆z)( − y
∫ H e ) ∆y
1
= ( x, yz , )( − z
∫ H e ) ∆z
4
3
= ( x, y +∆y, z) z
∫ H e ∆z
2
2
= ( x, yz , ) y
∫ H e ∆y
1
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 12

Die Maxwellschen Gleichungen in differentieller Form
x
∫ H
d s
= G
d A = Ge
∆y∆ z = Gx∆y∆z
= H( x, y, z) ey∆ y + H( x, y +∆y, z) ez∆ z+ H( x, y, z+∆z)( −ey) ∆ y + H( x, y, z)( −ez)
∆z
= H( xyz , , ) ∆ y+ H( xy , +∆yz , ) ∆z− H( xyz , , +∆z) ∆y−H( xyz , , ) ∆z
y z y z
∂Hz
∂Hy
= Hz( x, y, z) + ∆y
= Hy
( x, y, z)
+ ∆z
∂y
∂z
⎡
∂Hy
⎤ ∂Hy
= ⎢Hy( x, y, z) −Hy( x, y, z)
− ∆z ∆ y = − ∆z∆y
z
⎥
⎣
∂ ⎦ ∂z
⎡
∂Hz
⎤ ∂Hz
= ⎢Hz( x, y, z) + ∆y −Hz( x, y, z)
∆ z = ∆y∆z
y
⎥
⎣
∂
⎦ ∂y
∂H
∂H
= d = ∆y∆z = Gx∆y∆z
∂z
∂y
y
z
d =− ∆z∆ y + ∆y∆z
x
∫ H s
G A Ge
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 13

Die Maxwellschen Gleichungen in differentieller Form
∂H
∂H
= d = ∆y∆z = Gx∆y∆z
∂z
∂y
y
z
d =− ∆z∆ y + ∆y∆z
x
∫ H s
G A Ge
Division durch ∆y∆z:
∂H
∂y
z
∂H
y
− =
∂z
G
x
∆ A= ey∆ Ay
= ey∆ ∆
z x
∆ A= ez∆ Az
= ez∆ ∆
Für den Fall 2 (Fläche in der zx-Ebene) und den Fall 3 (Fläche in der xy-Ebene)
erhält man analog (bzw. durch zyklisches Vertauschen der Indizes):
x y
∂H
∂z
x
∂H
∂x
z
− =
G
y
x
∂H
y
∂x
∂H
∂y
x
− =
G
z
y
z
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 14

Die Maxwellschen Gleichungen in differentieller Form
∂H
∂y
z
∂H
y
− =
∂z
G
x
⋅e
x
∂H
∂z
x
∂H
∂x
z
− =
G
y
⋅e
y
∂H
y
∂x
∂H
∂y
x
− =
G
z
⋅e
z
⎛∂H ∂H
z y ⎞ ⎛∂H H
x
∂Hz ⎞ ⎛∂
y ∂H
⎞
x
∂D
⎜ − x + ⎜ − ⎟ y + − z = = +
∂y ∂z ⎟e e
∂z ∂x ⎜
∂x ∂y ⎟e G J
⎝ ⎠ ⎝ ⎠ ⎝ ⎠
∂t
⎛∂H
∂H
z y ⎞
⎜ −
∂y
∂z
⎟
⎜ ⎟
⎜∂Hx
∂Hz
⎟
rotH
= ⎜ −
∂z
∂x
⎟
⎜ ⎟
⎜∂Hy
∂Hx
−
⎟
⎜ ∂x
∂y
⎟
⎝ ⎠
als Spaltenvektor
= rotH
Rotation von H
ex ey ez
∂ ∂ ∂ ∂
∂ ∂ ∂
∂ ∂
rotH
= = ex ∂y ∂z − ey ∂x
∂z
+ ez
∂x ∂y
∂ x ∂ y ∂ z
H H
y
Hz x
Hz
Hx Hy
Hx Hy Hz
a11 a12
in Determinantenschreibweise
a a a a
a a = −
21 22
11 22 12 21
"Hauptdiagonale – Nebendiagonale"
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 15

Die Maxwellschen Gleichungen in differentieller Form
Berechnung einer 3-reihigen Determinante nach der Regel von Sarrus
aus:
Papula
Mathematische Formelsammlung
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 16

Die Maxwellschen Gleichungen in differentieller Form
1. Maxwellsche Gleichung (1. Hauptgleichung)
∂D
rotH
= J + Differentielles Durchflutungsgesetz
∂ t
∫
L
Integrale Form:
⎛ ∂D
⎞
Hds = ∫⎜J + ⎟dA
⎝ ∂t
A ⎠
"Der Wirbel der magnetischen Feldstärke ist in jedem Punkt des Raumes gleich
der Gesamtstromdichte (Leitungs- und Verschiebungsstrom) in diesem Punkt."
Eigenschaften der Rotation:
• Der Operator "rot" ist ein Differentialoperator 1. Ordnung.
• Die Bezeichnung "Rotation" stammt aus der Hydrodynamik und beschreibt dort
die Bildung von "Wirbeln" (geschlossene Feldlinien in den Geschwindigkeitsfeldern
strömender Flüssigkeiten).
•Der Vektor (!) rot H
heißt auch "Wirbeldichte" oder "Wirbelfeld" zu H
.
• Ein Vektorfeld, dessen Rotation verschwindet, heißt wirbelfrei.
• Der Betrag der Rotation ist ein Maß für die "Wirbelstärke" des Feldes.
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 17

Die Maxwellschen Gleichungen in differentieller Form
Analog lässt sich aus der integralen Form der 2. Maxwellschen Gleichung
d
∫Eds
=− d
dt
∫B A unmittelbar die differentielle Form ableiten:
L
2. Maxwellsche Gleichung (2. Hauptgleichung)
∂B
rotE =− ∂ t
A
Differentielles Induktionsgesetz
"Der Wirbel der elektrischen Feldstärke ist in jedem Punkt des Raumes gleich
der Abnahmegeschwindigkeit der magnetischen Flussdichte in diesem Punkt."
Bei Abwesenheit zeitlich veränderlicher magnetischer Felder:
rotE
= 0
"Das elektrostatische Feld ist wirbelfrei."
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 18

Die Maxwellschen Gleichungen in differentieller Form
Ähnliche Vorgehensweise wie für die 1. und 2. Maxwellsche Gleichung nun für
die 4. Maxwellsche Gleichung bzw. den Gaußschen Satz: ∫ D
d A= Q
An Stelle eines beliebigen Volumens Betrachtung eines quaderförmigen
Volumenelements ∆V = ∆x∆y∆z
A
Für die linke Seite der Gleichung:
1. Fall Flächen in der xz-Ebene:
D( x, yz , )( −ey) ∆ A + D( xy , +∆yz , ) ey∆A
y
= −D ( x, y, z) ∆z∆ x+ D ( x, y +∆y, z)
∆z∆x
y
y
⎡
∂Dy
⎤
= ⎢Dy
( x, y, z)
+ ∆y
∂y
⎥
⎣
⎦
⎡
∂Dy
⎤
= −Dy( x, y, z) ∆z∆ x+ ⎢Dy( x, y, z)
+ ∆y z x
y
⎥∆ ∆
⎣
∂ ⎦
∂Dy
∂D y z x
y
= ∆ ∆ ∆ = ∆ V
∂y
∂y
y
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 19

Die Maxwellschen Gleichungen in differentieller Form
∂D
y
∂y
∆ V
= Beitrag des Flächenelements in der xz-Ebene zur linken Seite der Glg.
Entsprechende Beiträge liefern die Flächen in der xy- und der yz-Ebene
insgesamt für die linke Seite der Gleichung:
∫ D
d A
A
⎛∂D
∂D
∂D
⎜
⎝ ∂x ∂y ∂z
⎞
⎟
⎠
x y z
= + + ∆
V
= divD
Divergenz von D
⎛∂D
∂D
x y ∂D
⎞
z
divD
= ⎜ + +
x y z
⎟
⎝ ∂ ∂ ∂ ⎠
Eigenschaften der Divergenz:
• Der Operator "div" ist ein Differentialoperator 1. Ordnung.
• Die Bezeichnung "Divergenz" stammt aus der Hydrodynamik und bedeutet
Auseinanderströmen ("Divergieren") einer Flüssigkeit.
•Der Skalar (!) div D
heißt auch "Quelldichte" oder "Quellstärke pro Volumeneinheit".
• Ein Vektorfeld, dessen Divergenz verschwindet, heißt quellenfrei.
• Ist in einem Punkt des Raumes die Divergenz > 0, so hat das Vektorfeld dort eine
Quelle. Ist die Divergenz < 0, so hat das Vektorfeld dort eine Senke.
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 20

Die Maxwellschen Gleichungen in differentieller Form
Damit also für die linke Seite der Gleichung:
∫ D
d A = div D
⋅∆V
A
Für die rechte Seite der Gleichung ergibt sich für das betrachtete infinitesimal
kleine quaderförmige Volumenelement ∆V mit der Raumladungsdichte ρ:
∫
Q = ρdV = ρ∆x∆y∆ z = ρ∆V
V
Aus
∫ D
d A= Q wird also divD ⋅ ∆ V = ρ∆V
divD
= ρ
A
Analoge Vorgehensweise für die 3. Maxwellsche Gleichung:
∫ B
Aus d A = 0 wird divB
= 0
A
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 21

Die Maxwellschen Gleichungen in differentieller Form
3. Maxwellsche Gleichung (1. Nebenbedingung)
divB
= 0
"Die Quelldichte der magnetischen Flussdichte ist in jedem Punkt des Raumes
stets gleich Null."
4. Maxwellsche Gleichung (2. Nebenbedingung)
divD
= ρ
"Die Quelldichte der elektrischen Verschiebungsdichte ist in jedem Punkt des
Raumes gleich der Raumladungsdichte in diesem Punkt."
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 22

Die Maxwellschen Gleichungen in differentieller Form
Schreibweise bei harmonischer Zeitabhängigkeit
1. Maxwellsche Gleichung bei harmonischer Zeitabhängigkeit:
∂D
rotH
= J + rotH = J + jωD = γE + jωεE = ( γ + jωε)
E
∂ t
2. Maxwellsche Gleichung bei harmonischer Zeitabhängigkeit:
∂B
rotE =− rotE
=−jωµ
H rotE
=−jωµ
H
∂ t
rotH
= +
( γ jωε
)
vereinfachte komplexe
Schreibweise
vereinfachte komplexe
Schreibweise
E
3. Maxwellsche Gleichung bei harmonischer Zeitabhängigkeit:
divB
= 0 divB = 0
divB = 0 divµ H
= 0
4. Maxwellsche Gleichung bei harmonischer Zeitabhängigkeit:
divD = ρ divD = ρ
divD = ρ divε E
= ρ
vereinfachte komplexe
Schreibweise
vereinfachte komplexe
Schreibweise
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 23

Bedeutung der Maxwellschen Gleichungen
Alle elektromagnetischen Erscheinungen
(in ruhender Materie) sind auf die
Maxwellschen Gleichungen der Elektrodynamik,
also auf sieben Grundgleichungen,
zurückführbar.
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 24

Bedeutung der Maxwellschen Gleichungen
Einteilung der Felder aus mathematischer Sicht:
1) wirbelfreie Felder (reine Quellenfelder)
2) quellenfreie Felder (reine Wirbelfelder)
3) Wirbelfelder (Felder mit Quellen und Wirbeln)
Einteilung der Felder aus physikalischer Sicht:
1) stationäre Felder
a) stationäre elektrische Felder
α) elektrostatisches Feld (J = 0)
β) Strömungsfeld (J ≠ 0)
b) stationäre magnetische Felder
α) magnetostatisches Feld (J = 0)
β) Magnetfeld (J ≠ 0)
2) nichtstationäre Felder
a) quasistationäres Feld
b) schnellveränderliches Feld
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 25

Anwendungsbeispiel: zeitlich veränderliche Felder
1. MG
2. MG
3. MG
4. MG
rotH
= +
rotE
( γ jωε
)
=−jωµ
H
divµ H
= 0
divε E
= ρ
E
Annahmen: harmonische Zeitabhängigkeit, nichtleitendes homogenes Material
(d.h. γ = 0, ε = const., µ = const.):
rotH
= jωε E
rotE
=−jωµ
H
divH
alle Vektoren = komplexe Amplituden
= 0
ρ
divE
=
ε
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 26

Anwendungsbeispiel: zeitlich veränderliche Felder
1) rotH
= jωε E
Frage: sind Longitudinalwellen möglich?
Longitudinalwelle heißt: E = ezE( z)
(nur z-Komponente)
a) Einsetzen in 2):
∂ ∂
0 0 0 0
= ex ∂z
− ey ∂z
+ ez
0 0
0 Ez
0 Ez
ex ey ez ex ey ez
∂ ∂ ∂
∂
rotE
= = 0 0 = 0 = −jωµ
H
∂x ∂y ∂z
∂z
E E E 0 0 E
x
y
2) rotE
=−jωµ
H
z
Das vorausgesetzte Feld ist wirbelfrei. Es ist
nicht mit einem Magnetfeld verknüpft, entsteht
also nicht durch Änderung eines magnetischen
Flusses.
z
3) divH
= 0
4) divE
=
ρ
ε
Eine Longitudinalwelle schwingt in
Ausbreitungsrichtung der Welle.
Eine Transversalwelle schwingt
senkrecht zur Ausbreitungsrichtung
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 27

Anwendungsbeispiel: zeitlich veränderliche Felder
1) rotH
= jωε E 2) rotE
=−jωµ
H
Longitudinalwelle heißt: E = ezE
( z)
b) Einsetzen in 4):
z
3) divH
= 0
4) divE
=
ρ
ε
div
⎛∂E ∂E
∂E ⎞ ∂E
⎜
x y z
⎟
⎝ ∂ ∂ ∂ ⎠ ∂z
E Das vorausgesetzte Feld lässt sich dagegen durch eine
x y z z
= + + = =
ρ
ε
1
E ( ) .
z
z = ρdz + const
ε ∫
Das vorausgesetzte Feld lässt sich dagegen durch eine
bestimmte Ladungsverteilung im Raum realisieren.
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 28

Anwendungsbeispiel: zeitlich veränderliche Felder
1) rotH
= jωε E
a) Einsetzen in 2):
2) rotE
=−jωµ
H
3) divH
= 0
ex ey ez ex ey ez
∂ ∂ ∂
∂ ∂E
x
rotE = = 0 0 = ey
= −jωµ
H
∂x ∂y ∂z
∂z ∂z
E E E E 0 0
x
y
z
x
x
4) divE
=
Frage: sind Transversalwellen möglich?
Transversalwelle heißt z.B.: E = exE
( z)
(hat x-Komponente)
Auf der linken Seite nur y-Komponente auf der rechten Seite kann nur H y
von
Null verschieden sein:
∂E
∂z
x
=−jωµ
H
y
∂
∂
0 0 0 0
= ex ∂z
− ey ∂z
+ ez
Ex
0
0 0 E 0
x
Gleichung mit zwei Unbekannten 2. Gleichung erforderlich 1)
ρ
ε
Eine Longitudinalwelle schwingt in
Ausbreitungsrichtung der Welle.
Eine Transversalwelle schwingt
senkrecht zur Ausbreitungsrichtung
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 29

Anwendungsbeispiel: zeitlich veränderliche Felder
1) rotH
= jωε E
2) rotE
=−jωµ
H
3) divH
= 0
∂z
∂z
ex ey ez
Hy
0 0 0
∂ ∂H
y
rotH = 0 0 = − e = jωε
E = jωε
e E
∂z
∂z
0 H 0
y
x x x
4) divE
=
Da das magnetische Feld senkrecht auf dem elektrischen steht:
∂ ∂
0 0 0 0
= ex − ey + ez
0 H
y
ρ
ε
H
=
eyH
( ) y
z
∂H
y
∂z
=−jωε
E
x
bereits hergeleitet:
∂E
∂z
x
=−jωµ
H
y
Da nur eine Abhängigkeit von z (Ausbreitung in z-Richtung!) besteht:
dH
dz
y
=−jωε
E
x
dE
dz
x
=−jωµ
H
y
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 30

Anwendungsbeispiel: zeitlich veränderliche Felder
dHy
dEx
+ jωεEx
= 0
+ jωµ
Hy
= 0
dz
dz
Differentiation nach z:
Differentiation nach z:
dE
Einsetzen von x
:
dz
2
dHy
jωε ( jωµ
Hy
)
dz
2
dHy
2
− γ H 0
2 y
=
dz
2
dHy
dEx
jωε
0
2
dz
2
dE
+ = x
dH
+ jωµ
y
=
dz
dz dz
2
0
γ
2
=
mit
jωµ jωε
( ⇒ γ = jω µε = jβ, ( α = 0), vgl. ETiT II_20)
2
0
dH
Einsetzen von
y
:
dz
2
dEx
+ jωµ − jωε
Ex
=
dz
+ − = ( )
Ausbreitungskonstante, vgl. ETIT II_20
Wellengleichungen, vgl. ETIT II_20!
2
0
2
dEx
2
− γ E 0
2 x
=
dz
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 31

Anwendungsbeispiel: zeitlich veränderliche Felder
2
dHy
2
− γ H 0
2 y
=
dz
2
dEx
2
− γ E 0
2 x
=
dz
Allgemeine Lösung für E x
(s. ETIT II_20):
E( z)
= Ce + Ce = Ce + Ce
x
γ z −γz jβz −jβz
1 2 1 2
rücklaufende hinlaufende
Welle
γ z
E ( z)
= E e + E e
x r h
−γ
z
dE
dz
=−jωµ
H
x
Einsetzen in die bereits hergeleitete Beziehung y :
dEx
= γ Ee − γEe = −jωµ
H
dz
γ
γz
−γz
Hy = ( − Ere + Ehe
)
jωµ
γz
−γz
r h y
γ jω µε µε ε 1
= = = = (s. ETIT II_22)
jωµ jωµ µ µ Z
F
Er
γ z Eh
Hy
( z)
=− e + e
Z Z
F
F
−γ
z
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 32

Anwendungsbeispiel: zeitlich veränderliche Felder
γ z −γ
z
Er
γ z Eh
Ex( z)
= Ere + Ehe
Hy
( z)
=− e + e
Z Z
Überprüfung: sind die 3. und die 4. Maxwellsche Gleichung erfüllt?
3) divH
= 0
⎛∂H
∂H ( )
x y ∂H
⎞ ∂Hy
z
z
divH
= + + = = 0
⎜
x y z
⎟
⎝ ∂ ∂ ∂ ⎠ ∂y
4) div E = ρ = 0 (wegen Raumladungsfreiheit)
ε
⎛∂E ∂Ey
div ( )
x
∂E ⎞
z
∂Ex
z
E = ⎜ + + = = 0
∂x ∂y ∂z ⎟
⎝
⎠ ∂x
F
F
−γ
z
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 33

Anwendungsbeispiel: zeitlich veränderliche Felder
γ z −γ
z
Er
γ z Eh
Ex( z)
= Ere + Ehe
Hy
( z)
=− e + e
Z Z
F
F
−γ
z
Die beiden Gleichungen beschreiben die Ausbreitung einer
elektromagnetischen Welle als Transversalwelle (TEM-Welle; TEM für
transversal elektro-magnetisch) im Raum.
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 34

Anwendungsbeispiel: zeitlich veränderliche Felder
Wellenausbreitung von einem Hertz'schen Dipol
Der Hertzsche Dipol (elektrischer
Elementardipol) ist ein fiktiver Strahler,
dessen Länge infinitesimal kurz ist und bei
dem eine konstante Stromverteilung
angenommen wird. In der Praxis kann er
durch einen Dipol angenähert werden,
dessen Länge l klein gegenüber der
Wellenlänge λ ist.
Hertzscher Dipol im Kugelkoordinatensystem
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 35

Anwendungsbeispiel: zeitlich veränderliche Felder
E-Feld
H-Feld
Nahfeld Fernfeld
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 36

Letzte Vorlesungsfolie ETIT II !!!
Fachgebiet
Hochspannungstechnik
ETIT II / VL 24 37