Kräfte am starren Körper

Kräfte am starren Körper
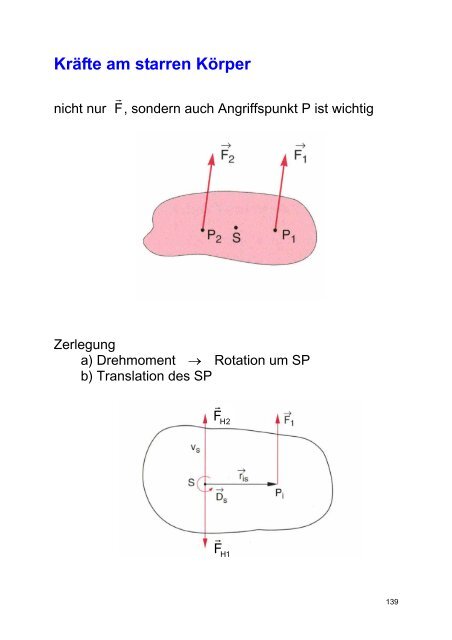
nicht nur F , sondern auch Angriffspunkt P ist wichtig
Zerlegung
a) Drehmoment → Rotation um SP
b) Translation des SP
F H2
F
H1
139

keine Wirkung der beiden „Hilfskräfte“ ( FH,1 FH,2
0)
d.h. keine zus. Translation / Rotation
+ = ,
F
und F bilden ein Kräftepaar
1 H,1
( is 1) ( is H,1)
D =
1
r × F −
1
r × F
2 2
oder mit F1 = -FH,1
( )
D = r × F = D → Rotation um Achse durch SP
is 1 S
F
= M a → Translation des Körpers
H,2 S
Ein ruhender Körper erfährt durch eine Kraft eine
Translation seines Schwerpunktes S sowie eine Rotation
um S
140

Spezialfall: beliebige Kraft bei Fixierung einer
r = r p,S
raumfesten Drehachse durch den SP ( )
( )
D = r× F= r× F + F + F
z n t
D = r× Fz + r× Fn + r×
Ft
D = r× Fz
≠ 0 aber unwirksam wg. Lagerung
( F z
= M a S
: Translation durch
Lagerung verhindert)
D = r× Fn
= 0 ( F n
= M a S
: aber Verschiebung durch
Lagerung verhindert)
D = r× Ft
≠ 0 Drehung um Achse
nur die Tangentialkomponente von F trägt zur Rotation
bei
141

Drehmomente durch die Schwerkraft
Bei Lagerung im SP heben sich alle Drehmomente auf:
∑ ∑
D = ri× dFi = ri×
g dm
i
i
i
∑→∫
D
=− g×∫
r
dm
D =− g× Mr S
= 0 da r = 0 S
Bei der Lagerung im Schwerpunkt wirken durch die
Schwerkraft keine Drehmomente (die Lage des Körpers
ist stabil)
142

Trägheitsmoment
ausgedehnter Körper, der sich um eine feste Achse
dreht
∆E kin, i = ½ ∆m i v i
2
da v i = r i × ω i
und r i = r i, z + r i, y + r i, x
oder r i, y + r i, x = r i, ⊥ wird
(r i, ⊥ Abstand von Drehachse)
∆E kin, i = ½ ∆m i [(r i, z + r i, ⊥) × ω i ] 2
da r i, z × ω i = 0 wird
∆E kin, i = ½ ∆m i ⋅ r i, ⊥ 2 ⋅ ω i
2
oder für einen ausgedehnten Körper
E kin = E rot =
lim ∑
∆m→(½ 0 i ∆m i r i, ⊥ 2 2
ω ) i
i
E rot = ½ ω 2 ∫ r 2 ⊥ ρ dV ω
i
=ω∀
i
I = ∫ r ⊥ 2 ρ dV = Trägheitsmoment
E rot = = ½ ω 2 I
I wird bestimmt durch die Abstandsverteilung der
Massen um gegebene Drehachse
143

Bsp.:
Trägheitsmoment einer homogenen Kugel
r = ⊥
a = rsin ϑ
I
R π 2π
2 2 2
=ρ⋅ r sinϑ ⋅r sinϑdr dϕdϑ
∫∫∫
r= 0ϑ= 0ϕ=
0
R π 2π
4 3
=ρ⋅ r sinϑ dr dϕdϕ
∫∫∫
r= 0ϑ= 0ϕ=
0
π
1 R
5 2 sin
3 d
= ρ ⋅ π ϑ ϑ
5
∫
0
8
15
5
= ρ⋅R
⋅π
M
4
= ρ⋅ π R
3
3
=
2 MR
2
5
weitere Beispiele siehe Demtröder ab S. 142
144

Zusammenfassung:
Dynamik der Drehbewegung
wird wesentlich bestimmt durch
die Dichte-Verteilung der Masse
gleiche Masse, verschiedene Masse-Verteilung
⇒ verschiedenes Trägheitsmoment
kinetische Energie bei Drehbewegung
(bzw. Rollbewegung) darstellen durch
Translation des Schwerpunktes
und
Rotation um Achse durch Schwerpunkt
(hier: Trägheitsmoment wichtig)
145

Drehimpuls ausgedehnter starrer Körper
für Massenpunkt gilt: L = m (r × v)
also auch
L i = ∆m i r i × v i
L i = ∆m i r i × (ω i × r i )
L i
= ∆m 2
i r ⊥
⋅ω
i
i
L =
∑ L i
=
i
∑ ∆m 2
i ri
⊥
ω i = ω
i
∑ ∆m i
i
r
2
i⊥
→
lim
∆m→0
i
L = ω ∫ r 2
⊥
ρ dV
ρ∆V i
L = I ω E rot = ½ ω 2 I = L 2 /2I
===========================================
Translation
Rotation
---------------------------------------------------------------------------
Masse m
Trägheitsmoment I
Impuls p
Kraft F
Geschwindigkeit v
Drehimpuls L
Drehmoment D
Winkelgeschwindigkeit ω
Beschleunigung x Winkelbeschleunigung ϕ
===========================================
äquivalente Größen
146

„Übersetzungen”
E kin = ½ m v 2 E rot = ½ I ω 2
p = m v L = r × p L = I ω
F = m x D = r × F D = I ϕ
Translation
Rotation
147

sei Drehmoment D = 0 ⇒ Drehimpuls L bleibt konstant
Veränderung der Massenverteilung führt zu einer
Veränderung des Trägheitsmomentes
Bsp.:
I 1
r 1
ω 1
I
r 2
< I
ω
2
> ω1
2 1
⇒ Veränderung von ω
2 2
E = ω I = L /2I
=
I 1
2
L
4mr
1
rot 2
2
= m ⋅ r + m ⋅ r = 2mr
2 2 2
1 1 2 1 1
I 2
=
2
2mr 2
148

Energiebilanz beim
Drehstuhlversuch mit Hanteln
E rot,1 = ½ I 1 ω 1
2
E rot,2 = ½ I 2 ω 2
2
hier angenommen: (I 1 / I 2 ) > 1
I 1 = Kugel weit draußen, Drehung langsam
I 2 = Kugel innen, Drehung schnell
Zusammenhang I i ←→ ω i gegeben durch
Drehimpulserhaltung: L 1 = I 1 ω 1 = I 2 ω 2 = L 2
ω 2 = (I 1 / I 2 ) ω 1
E rot,2 = ½ I 2 ω 2 2 = ½ I 2 (I 1 / I 2 ) 2 ω 1
2
E rot,2 = ½ I 1 (I 1 / I 2 ) ω 1 2 = E rot,1 (I 1 / I 2 )
da (I 1 / I 2 ) > 1 → E rot,2 > E rot,1
?? wo kommt die Energie her ??
149

Beim Heranziehen der Hanteln:
Arbeit gegen Zentrifugalkraft verrichten
r2 r2
∫ zentrifugal ∫
r
r
()
2
W =− F dr
= mω
r r dr
1 1
() ⎡I( ) I()
2 2
ω r = ω
1⎣ r
1
/ r ⎤⎦ = ω ⎡
1⎣ r
1
/r ⎤
⎦
(für Punktmassen)
r
2
( ) ⎡ I ( )
2 2 2
W = mω1I
r1
∫ ⎣
r/ r ⎤
⎦
dr
I 2 ∝ r
4
r
1
r
2 3 2 2
( 1/m ) ∫
⎡
⎣
1/r ⎤
⎦
dr ( 1/m ) ( 1/r )
⇒ =
( ) 2 ⎡I( ) ⎤( 2 2
)
W = I r ω ⎣ r /m⎦
1/r −1/r
1 2 1 1 1 2 1
W = E ⎡
rot,1 ⎣
r
1
/mr1 ⎦
r
1
/r2
−1
2 2 2
I ( ) ⎤( )
( I I )
W = E / − 1 = ∆ E
rot,1 1 2 rot,1
r
2 2
1
r
1 2
r
1
150

Steiner’scher Satz
Verbindung von
I B um beliebige Achse B mit
I S des Körpers bezogen auf eine zu B parallele Achse
durch den Schwerpunkt
I B
= ∫ r 2 dm
∫
I B = ( r + )
I B
S
a 2 dm
2
2
∫rS
∫ ∫
= dm + a dm + 2a r dm
I S M 0
S
I B = I S + M a 2 (*)
wenn Trägheitsmoment um Achse durch SP bekannt →
Trägheitsmoment um beliebige dazu parallele Achse mit
(*) bestimmbar
151

152

Das Trägheitsmoment eines Körpers
ist immer
auf eine bestimmte Drehachse bezogen.
gegebene Massenverteilung,
verschiedene Drehachsen
⇒ verschiedene Trägheitsmomente !!
gegebene Drehachse,
verschiedene Massenverteilung
⇒ verschiedene Trägheitsmomente !!
Trägheitsmoment I berechenbar ....
.... wenn ρ (r) bekannt
bei symmetrischen Massenverteilungen relativ leicht
berechenbar
falls Drehachse nicht durch Schwerpunkt geht:
Steiner’schen Satz nutzen
153

Bsp.:
eines Stabes
Rotation um eine senkrechte Achse b am Ende
Lösung a) direkt
I B
L
1 1
=ρ⋅A⋅ ∫ x dx = ρ⋅A⋅ L = ML
3 3
0
2 3 2
Lösung b) mit Satz von Steiner
I S eines rotierenden Stabes:
1 ML
2
12
I B = I S
⎛L
⎞
+ M ⎜ 2 ⎟
⎝ ⎠
1 1 1
= ML + ML = ML
12 4 3
2
2 2 2
154

Bsp. 2: Rollende Zylinder:
D = I ϕ ( = I ω )
mit Steinerschem Satz über Trägheitsmomente:
M g r sin α = (I S + M r 2 ) ω
Translationsbewegung des Schwerpunktes:
a S = s = r ω = r
M g r sinα
g sinα
=
2 2
( I + M r ) 1 + ( I / M r )
S
je größer das Trägkeitsmoment I S , desto geringer a S
E pot (s) = E kin (s) + E rot (s) = M g s sin α
1 2
1
Ekin
( s) = Mvr
, E I 2
rot
= ω
2
2
1 2 1 2
Mvr
I Mg s sin
2 + 2
ω = ⋅ ⋅ α v
ω=
r
r
2 2 I
vr + vr ⋅ = g⋅s⋅sinα
2
Mr
S
⇒
v
2gs sinα
=
1 + ( I / M r )
2
r 2
S
(rollend)
gleitend: M g s sin α = ½ M v 2
→
v = 2 g s sinα>
v
2 2
g
r
155

Bewegungsgleichung der Rotation
L i = r i, ⊥ × p i = ∆m i (r i, ⊥ × v i ) = ∆m i r i, ⊥ 2 ω
L
i
= ∆m i (r i, ⊥ × v
i) = r i, ⊥ × F i,t = D i, ∥
D i, ∥ = ∆m i r i, ⊥ 2
ω
D ∥ = (∑ ∆m i r i, ⊥ 2 ) ω = ω ∫r ⊥
2
dm = ω I
D ∥ = I ϕ vergleiche F = m r
für D ∥ = const.
ϕ(t) = ½ (D/I) t 2 + ω o t + ϕ o
Bewegungsgleichung (Winkelkoordinate)
156

Experimentelle Bestimmung des
Trägheitsmomentes eines Körpers
Rückstelldrehmoment proportional zu ϕ
D = - D r ϕ D r = „Richtmoment“
Bewegungsgleichung: I
o
ϕ = − D ϕ ma = F
I o = Trägheitsmoment des Drehtisches
r
D r
I O
ϕ =+ ϕ =0
Lösung der Schwingungsgleichung:
( t )
ϕ=ϕ sin ω , r
max I O
D
ω= harmonische Schwingung
2π
Schwingungsdauer T = = I
ω
/ D
o o r
157

Zusatzmasse mit bekanntem I A (M,R M )
T 1 = 2 π ( I + I ) / D
o A r
T 1 2 – T o 2 = (2 π ) 2 [ (I o + I A ) / D r - I o / D r ]
T 1 2 – T o 2 = (2 π ) 2
I A / D r
⇒ Messung von T 1 und T o liefert D r
⇒ T o liefert I o
158

Beziehung zwischen der momentanen Winkelgeschwindigkeit
ω und dem Drehimpuls L
es gilt: im Allgemeinen muss der Drehimpuls L
eines
beliebig starren Körpers nicht parallel zur
momentanen Drehachse, d.h. parallel zu ω
sein!
Der Zusammenhang zwischen den Vektoren ω
und L ist bestimmt durch die Massenverteilung
im starren Körper
Ziel: allgemeine Aussagen über Trägheitsmomente
eines gegebenen Körpers
es gibt „beliebig viele“ Drehachsen!
→ ?? → beliebig viele (unabhängige)
Trägheitsmomente?
(durch Steiner’schen Satz reduzierbar auf beliebige
Achse durch den Schwerpunkt)
Ergebnis:
Problem ist reduzierbar auf Trägheitsmoment für
Drehung um drei ausgezeichnete Achsen:
Hauptträgheitsachsen
mit
Hauptträgheitsmomenten
159

Das Ziel: Verstehen der
„Hauptachsen“ für Trägheitsmomente
beliebig geformter Körper
Achse ˆω durch den Schwerpunkt
Trägheitsmoment hängt ab
von Richtung ˆω der Achse
Ergebnis:
Es gibt eine Achse ˆω, bzgl. derer das
Trägheitsmoment MAXIMAL wird: I max
( ˆω
max
)
Es gibt eine Achse ˆω, bzgl. derer das
Trägheitsmoment MINIMAL wird: I min
( ˆω
min
)
wobei
ˆ
ˆ
min max
ω ⊥ ω
für die Drehung um die Achse
inter min max
ω ˆ = ω ˆ ×ω ˆ gilt
( ωˆ ) ≤ ( ωˆ ) ≤ ( ωˆ
)
I I I
inter min inter int er max max
160

Vektorbeziehung
D = A × B × C = A × ( B × C )
Aussage über D ?
B ⊥ B × C
C ⊥ B × C
D ⊥ B × C
D ⊥ A
daher muss D in der von B und C aufgespannten
Ebene liegen
→
D = λ B B + λ C C
Rechnung zeigt:
A × B × C = (A ⋅ C) B - (A ⋅ B) C
161

für jedes Massenelement
∆ mi
gilt:
A B C
L i = ∆m i ( r i × v
i
) = ∆m i ( r i × (ω × r i ))
Umformung mit Vektorrelation:
L i = ∆m i (r 2 i ω
- ( r i
ω) r i ) →
∫
( ÷ )dm
also für Körper insgesamt gilt:
L = ∫ (r 2 ω - (r ω ) r ) ρ dV ρ =ρ( r
)
r ⋅ω
L x = ∫[ r 2 ω x - (x ω x +y ω y +z ω z ) x ] ρ dV
Beim starren Körper hängt ω nicht vom Ort ab, d.h. die
Komponenten von ω dürfen vor die Integrale genommen
werden.
L x = ω x ∫ (r 2 - x 2 ) ρ dV - ω y ∫xy ρ dV - ω z ∫xz ρ dV
y
+ z
2 2
L x = I xx ω x + I xy ω y + I xz ω z
162

wobei:
I xx = ∫(r 2 - x 2 ) ρ dV
I xy = - ∫xy ρ dV
I xz = - ∫xz ρ dV
= I yx
= I zx
entsprechend ergibt sich
I yy = ∫(r 2 - y 2 ) ρ dV
I zz = ∫(r 2 - z 2 ) ρ dV
I yz = - ∫yz ρ dV
= I zy
L y = I yx ω x + I yy ω y + I yz ω z
L z = I zx ω x + I zy ω y + I zz ω z
163

L = (L x , L y, L z )
L x = I xx ω x + I xy ω y + I xz ω z
L y = I yx ω x + I yy ω y + I yz ω z
L z = I zx ω x + I zy ω y + I zz ω z
L x I xx I xy I xz ω x
L y = I yx I yy I yz ⋅ ω y
L z I zx I zy I zz ω z
L = I ω
I = Trägheitstensor
(symbolische Schreibweise für 3 Gleichungen)
164