Theorie Integralrechnung - hknoll.ch
Theorie Integralrechnung - hknoll.ch
Theorie Integralrechnung - hknoll.ch
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
Differentialre<strong>ch</strong>nung<br />
Mathematik<br />
97<br />
Es soll jetzt der Gesamtgewinn maximiert werden, wobei aber zu bea<strong>ch</strong>ten ist, dass die Arbeitszeit<br />
pro Wo<strong>ch</strong>e (s) limitiert ist.<br />
Als Zielfunktion wird der Gesamtgewinn G angesetzt. Er ist:<br />
G = g 1 x 1 + g 2 x 2<br />
Die Nebenbedingungen werden einerseits dur<strong>ch</strong> die maximale Laufzeit der Mas<strong>ch</strong>inen und andererseits<br />
dur<strong>ch</strong> die Tatsa<strong>ch</strong>e, dass Stückzahlen ni<strong>ch</strong>t negativ sind bestimmt.<br />
a 1 x 1 + b 1 x 2 ≤ s<br />
a 2 x 1 + b 2 x 2 ≤ s<br />
x 1 ≥ 0<br />
x 2 ≥ 0<br />
Für die konkrete Lösung seien nun folgende Zahlenwerte gegeben:<br />
a 1 = 2 min b 1 = 4 min g 1 = 4 Fr.<br />
a 2 = 6 min b 2 = 2 min g 2 = 3 Fr. s = 2400 min<br />
Damit ergeben si<strong>ch</strong> folgende Glei<strong>ch</strong>ungen und Unglei<strong>ch</strong>ungen:<br />
G = 4x 1 + 3x 2<br />
2x 1 + 4x 2 ≤ 2400<br />
6x 1 + 2x 2 ≤ 2400<br />
x 1 ≥ 0<br />
x 2 ≥ 0<br />
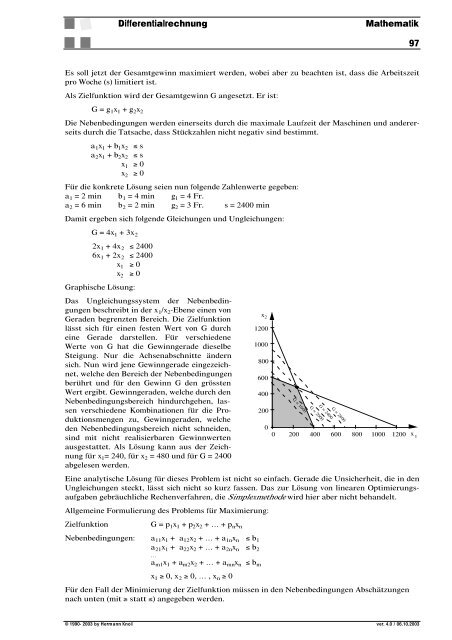
Graphis<strong>ch</strong>e Lösung:<br />
Das Unglei<strong>ch</strong>ungssystem der Nebenbedingungen<br />
bes<strong>ch</strong>reibt in der x 1 /x 2 -Ebene einen von<br />
Geraden begrenzten Berei<strong>ch</strong>. Die Zielfunktion<br />
lässt si<strong>ch</strong> für einen festen Wert von G dur<strong>ch</strong><br />
eine Gerade darstellen. Für vers<strong>ch</strong>iedene<br />
Werte von G hat die Gewinngerade dieselbe<br />
Steigung. Nur die A<strong>ch</strong>senabs<strong>ch</strong>nitte ändern<br />
si<strong>ch</strong>. Nun wird jene Gewinngerade eingezei<strong>ch</strong>net,<br />
wel<strong>ch</strong>e den Berei<strong>ch</strong> der Nebenbedingungen<br />
berührt und für den Gewinn G den grössten<br />
Wert ergibt. Gewinngeraden, wel<strong>ch</strong>e dur<strong>ch</strong> den<br />
Nebenbedingungsberei<strong>ch</strong> hindur<strong>ch</strong>gehen, lassen<br />
vers<strong>ch</strong>iedene Kombinationen für die Produktionsmengen<br />
zu, Gewinngeraden, wel<strong>ch</strong>e<br />
den Nebenbedingungsberei<strong>ch</strong> ni<strong>ch</strong>t s<strong>ch</strong>neiden,<br />
sind mit ni<strong>ch</strong>t realisierbaren Gewinnwerten<br />
ausgestattet. Als Lösung kann aus der Zei<strong>ch</strong>nung<br />
für x 1 = 240, für x 2 = 480 und für G = 2400<br />
abgelesen werden.<br />
1200<br />
1000<br />
800<br />
600<br />
400<br />
200<br />
0<br />
G = 2800<br />
G = 2400<br />
G = 2000<br />
G = 1600<br />
0 200 400 600 800 1000 1200<br />
Eine analytis<strong>ch</strong>e Lösung für dieses Problem ist ni<strong>ch</strong>t so einfa<strong>ch</strong>. Gerade die Unsi<strong>ch</strong>erheit, die in den<br />
Unglei<strong>ch</strong>ungen steckt, lässt si<strong>ch</strong> ni<strong>ch</strong>t so kurz fassen. Das zur Lösung von linearen Optimierungsaufgaben<br />
gebräu<strong>ch</strong>li<strong>ch</strong>e Re<strong>ch</strong>enverfahren, die Simplexmethode wird hier aber ni<strong>ch</strong>t behandelt.<br />
Allgemeine Formulierung des Problems für Maximierung:<br />
Zielfunktion<br />
G = p 1 x 1 + p 2 x 2 + … + p n x n<br />
Nebenbedingungen: a 11 x 1 + a 12 x 2 + … + a 1n x n ≤ b 1<br />
a 21 x 1 + a 22 x 2 + … + a 2n x n ≤ b 2<br />
…<br />
a m1 x 1 + a m2 x 2 + … + a mn x n ≤ b m<br />
x 1 ≥ 0, x 2 ≥ 0, … , x n ≥ 0<br />
Für den Fall der Minimierung der Zielfunktion müssen in den Nebenbedingungen Abs<strong>ch</strong>ätzungen<br />
na<strong>ch</strong> unten (mit ≥ statt ≤) angegeben werden.<br />
x 2<br />
x 1<br />
© 1990- 2003 by Hermann Knoll ver. 4.0 / 06.10.2003
Differentialre<strong>ch</strong>nung<br />
Mathematik<br />
98<br />
Differentiale<br />
Eine Funktion f(x) ist differenzierbar und hat<br />
die Ableitung f '(x). Geometris<strong>ch</strong> bedeutet die<br />
1. Ableitung bekanntli<strong>ch</strong> die Steigung der<br />
Tangente. Der Zweck des Differenzierens ist es<br />
ja immer gewesen, für ein sehr kleines Stück<br />
die Kurve dur<strong>ch</strong> ihre Tangente zu ersetzen.<br />
Mit der 1. Ableitung kann die Tangentenglei<strong>ch</strong>ung<br />
gebildet werden. Für einen sehr kleinen<br />
Forts<strong>ch</strong>ritt von x - wir nennen ihn hier dx<br />
oder Δx - wird si<strong>ch</strong> das y ni<strong>ch</strong>t sehr viel anders<br />
verändern, wenn wir die ursprüngli<strong>ch</strong>e Funktion<br />
oder ihre Tangente im Startpunkt verfolgen.<br />
Mit Δy bezei<strong>ch</strong>nen wir die effektive Veränderung<br />
des Funktionswertes bei einem Forts<strong>ch</strong>ritt<br />
um dx, dy soll die Veränderung des y-<br />
Wertes an der Tangente messen.<br />
x 1<br />
Δx = dx<br />
dy<br />
x 2<br />
Δy<br />
t<br />
y = f(x)<br />
y' = f '(x)<br />
Δy = y 2 - y 1 = f(x 2 ) - f(x 1 ) = f(x 1 + Δx) - f(x 1 )<br />
Δy<br />
Δx = f(x 1 + Δx) - f(x 1 )<br />
Δx<br />
dy<br />
dx = f '(x)<br />
dy = f '(x)•dx<br />
Beispiel 1:<br />
y = x 2 , x 1 = 2, Δx = dx = 0,01<br />
y' = 2x<br />
y'(2) = 4<br />
Δy = (2.01) 2 - 2 2 = 4,0401 - 4 = 0,0401<br />
dy = f '(2)•dx = 4•0,01 = 0,04<br />
Beispiel 2:<br />
y = ln x, x 1 = 0,1, Δx = dx = 0,01<br />
y' = 1 x<br />
y'(0,1) = 1<br />
0,1 = 10<br />
Δy = ln 0,11 - ln 0,1 = 0,095310<br />
dy = f '(0,1)•0,01 = 10•0,01 = 0,1<br />
Bei genügend kleinem Wert von dx = Δx ist der Unters<strong>ch</strong>ied zwis<strong>ch</strong>en Δy und dy sehr klein. Für<br />
praktis<strong>ch</strong>e Probleme liegt dieser Unters<strong>ch</strong>ied meist unterhalb der Genauigkeitss<strong>ch</strong>welle der Messwerte.<br />
© 1990- 2003 by Hermann Knoll ver. 4.0 / 06.10.2003
<strong>Integralre<strong>ch</strong>nung</strong><br />
Mathematik<br />
99<br />
Bestimmtes Integral<br />
Einführung<br />
1. Weg-Zeit-Funktion:<br />
Bei der glei<strong>ch</strong>förmigen Bewegung aber au<strong>ch</strong><br />
bei der glei<strong>ch</strong>mässig bes<strong>ch</strong>leunigten Bewegung<br />
kann man den in einer Zeitspanne Δt<br />
zurückgelegten Weg no<strong>ch</strong> re<strong>ch</strong>t einfa<strong>ch</strong> bere<strong>ch</strong>nen.<br />
Bei einer ni<strong>ch</strong>tlinearen Ges<strong>ch</strong>windigkeits-<br />
Zeit-Funktion gibt es aber Probleme. Die<br />
Ges<strong>ch</strong>windigkeit ist ja die Änderung des Weges<br />
Δs während einer kleinen Zeitspanne Δt: v = Δs<br />
Δt .<br />
Für Δs gilt: Δs = v•Δt<br />
Am besten wird das gesamte Zeitintervall in<br />
kleine Spannen Δt zerlegt. Die jeweils in<br />
diesen Zeitspannen Δt zurückgelegten<br />
Strecken Δs werden summiert. Für eine sehr<br />
feine Einteilung erhält man au<strong>ch</strong> sehr viele<br />
Summanden und das Ergebnis wird dem<br />
genauen Wert für den Weg sehr nahe kommen.<br />
v<br />
s ≈ ∑<br />
i=1<br />
n<br />
vi Δt i<br />
Δs = v•Δt<br />
v<br />
Δt<br />
t<br />
2. Arbeit im Gravitationsfeld:<br />
Bei der Bre<strong>ch</strong>nung der Hubarbeit im Gravitationsfeld<br />
bei grösserer Hubhöhe kann man die<br />
Änderung der Gravitationskraft mit dem Abstand<br />
r ni<strong>ch</strong>t mehr verna<strong>ch</strong>lässigen: F(r) = γ mM<br />
r 2<br />
F<br />
Au<strong>ch</strong> hier kann die Gesamtarbeit W als Summe<br />
der einzelnen Arbeitsportionen ΔW bere<strong>ch</strong>net<br />
werden. ΔW = F(r)Δr<br />
W ≈ ∑<br />
i=1<br />
n<br />
ΔWi = ∑<br />
i=1<br />
n<br />
n<br />
Fi (r)Δr i = ∑i=1<br />
γ mM<br />
r i<br />
2 Δr i<br />
Geometris<strong>ch</strong> bedeuten diese Summierungen<br />
eine Ber<strong>ch</strong>nung der Flä<strong>ch</strong>e zwis<strong>ch</strong>en einer<br />
Kurve und der Abszisse im entspre<strong>ch</strong>enden<br />
Abszissenabs<strong>ch</strong>nitt.<br />
r 1<br />
r 2<br />
r<br />
Flä<strong>ch</strong>enbere<strong>ch</strong>nung und bestimmtes Integral<br />
Gegeben ist eine in einem abges<strong>ch</strong>lossenen Intervall [a, b] stetige Funktion f(x). Gesu<strong>ch</strong>t ist der Inhalt<br />
der Flä<strong>ch</strong>e zwis<strong>ch</strong>en Kurve und x-A<strong>ch</strong>se im Intervall [a, b]. Zunä<strong>ch</strong>st sei zudem vorausgesetzt,<br />
dass f(x) streng monoton steigend sei und für alle x aus dem Intervall [a, b] f(x) ≥ 0 gelte.<br />
y<br />
y<br />
f(x )<br />
n-1<br />
f(x )<br />
n-1<br />
f(x )<br />
0<br />
f(x )<br />
1<br />
f(x ) i<br />
f(x )<br />
0<br />
f(x )<br />
1<br />
f(x ) i<br />
x 0<br />
x 1<br />
x i-1<br />
x i<br />
x n-1<br />
x n<br />
x<br />
x 0<br />
x 1<br />
x i-1<br />
x i<br />
x n-1<br />
x n<br />
x<br />
Δx 1<br />
Δx i<br />
Δx n<br />
Δx 1<br />
Δx i<br />
Δx n<br />
© 1990- 2003 by Hermann Knoll ver. 4.0 / 06.10.2003
<strong>Integralre<strong>ch</strong>nung</strong><br />
Mathematik<br />
100<br />
Die Flä<strong>ch</strong>e wird in Streifen mit der Breite Δx i eingeteilt. Werden jeweils mit den grössten Funktionswerten<br />
Re<strong>ch</strong>tecke gebildet, nennt man die Summe der Re<strong>ch</strong>tecksflä<strong>ch</strong>en Obersumme O n .<br />
Entspre<strong>ch</strong>end ist die Untersumme U n die Summe der Re<strong>ch</strong>tecke mit den jeweils kleinsten Funktionswerten<br />
in den einzelnen Streifen. Wählt man in jedem Streifen einen beliebigen Funktionswert<br />
f(ξi) aus, erhält man eine sogenannte Zwis<strong>ch</strong>ensumme F n .<br />
Es gilt: U n ≤ F n ≤ O n<br />
U n = ∑<br />
i=1<br />
n<br />
f(xi-1 )Δx i<br />
n<br />
O n = ∑ f(xi )Δx i<br />
i=1<br />
y<br />
f(ξ )<br />
n<br />
f(ξ ) i<br />
f(ξ 2<br />
)<br />
f(ξ 1<br />
)<br />
F n = ∑<br />
i=1<br />
n<br />
f(ξi )Δx i<br />
ξ 1<br />
ξ 2<br />
ξ i<br />
ξ n<br />
Δx 1 Δx i<br />
Δx n<br />
Nun wird die Einteilung verfeinert, d.h. die Anzahl der Streifen wird vergrössert, wobei aber die<br />
Streifen selbst s<strong>ch</strong>mäler werden. Dur<strong>ch</strong> diese Verfeinerung werden Obersumme, Untersumme und<br />
Zwis<strong>ch</strong>ensumme einen besseren Näherungswert für die gesu<strong>ch</strong>te Flä<strong>ch</strong>e geben als zuvor. Bildet man<br />
den Grenzwert mit n → ∞, wobei aber die Breite aller Streifen Δxi na<strong>ch</strong> Null gehen soll, erhalten wir<br />
einen genauen Wert für die gesu<strong>ch</strong>te Flä<strong>ch</strong>e. Es gilt:<br />
b<br />
lim U n<br />
n = lim O n = lim F n = lim<br />
n→∞ n→∞ n→∞ n→∞<br />
∑ f(ξi )Δx i = ∫<br />
i=1<br />
a<br />
f(x) dx<br />
Wir werden jetzt die oben getroffenen Eins<strong>ch</strong>ränkungen was das Vorzei<strong>ch</strong>en von f(x) und die<br />
Monotonie betrifft fallen lassen. Es sei also f(x) eine in einem abges<strong>ch</strong>lossenen Intervall [a, b] stetige<br />
Funktion. Es wird eine Einteilung in n Streifen mit der Breite Δxi vorgenommen. In jedem Streifen<br />
wird ein x-Wert ξ i ausgewählt. Der Funktionswert an der Stelle ξ i ist dann f(ξ i ). Die n-te<br />
Zwis<strong>ch</strong>ensumme F n ist somit:<br />
x<br />
F n = ∑<br />
i=1<br />
n<br />
f(ξi )Δx i<br />
Existiert der Grenzwert mit n na<strong>ch</strong> ∞ und Δx i na<strong>ch</strong> Null, so ist dieser Grenzwert das 'Integral der<br />
Funktion f(x) in den Grenzen von a bis b'.<br />
b<br />
n<br />
I = a<br />
∫f(x)dx = lim<br />
n→∞<br />
∑ f(ξi )Δx i<br />
i=1<br />
f(x) heisst Integrand, das Intervall von a bis b ist der Integrationsweg, a und b heissen Integrationsgrenzen<br />
und x ist die Integrationsvariable.<br />
b<br />
b<br />
b<br />
b<br />
∫f(x)dx = a<br />
∫f(u)du = a<br />
∫f(z)dz = a<br />
∫f(t)dt = …<br />
a<br />
Das bestimmte Integral wird ganz allgemein als Grenzwert einer Produktsumme definiert. Für bestimmte<br />
Eigens<strong>ch</strong>aften von f(x) (siehe oben) kann das Integral zur Bere<strong>ch</strong>nung von Flä<strong>ch</strong>en verwendet<br />
werden. In der Physik werden aber au<strong>ch</strong> andere Grössen als Integral definiert.<br />
Für die beiden Beispiele zur Einführung erhalten wir jetzt:<br />
Weg-Zeit-Funktion:<br />
t<br />
n 2v(t)dt<br />
s = lim<br />
n→∞<br />
∑ vi Δt i = ∫<br />
i=1<br />
t1<br />
Arbeit im Gravitationsfeld:<br />
n n<br />
W = lim<br />
n→∞<br />
∑ ΔWi = lim<br />
i=1 n→∞<br />
∑ Fi (r)Δr i =<br />
i=1<br />
n<br />
= lim<br />
n→∞<br />
∑i=1<br />
r 2<br />
γ mM<br />
r<br />
2 Δr i =<br />
i<br />
r1∫<br />
γ mM<br />
r 2 dr<br />
© 1990- 2003 by Hermann Knoll ver. 4.0 / 06.10.2003
<strong>Integralre<strong>ch</strong>nung</strong><br />
Mathematik<br />
101<br />
Integrationsregeln<br />
Konstanter Faktor:<br />
Summe und Differenz:<br />
Zerlegung des Integrationsintervalls:<br />
∫<br />
a<br />
b<br />
c•f(x)dx = c• ∫<br />
a<br />
b<br />
f(x)dx<br />
b<br />
b<br />
a<br />
∫ [ f(x) ± g(x) ] dx = a<br />
∫f(x)dx ± a<br />
∫<br />
bg(x)dx<br />
∫<br />
a<br />
c<br />
f(x)dx = ∫<br />
a<br />
b<br />
f(x)dx + ∫<br />
b<br />
cf(x)dx<br />
Vorzei<strong>ch</strong>en des Integrals:<br />
a < b ∧ f(x) > 0 ⇒ I > 0<br />
a < b ∧ f(x) < 0 ⇒ I < 0<br />
a > b ∧ f(x) > 0 ⇒ I < 0, weil alle Δx i < 0 sind<br />
a > b ∧ f(x) < 0 ⇒ I > 0<br />
Vertaus<strong>ch</strong>en der Grenzen:<br />
∫<br />
a<br />
b<br />
f(x)dx = - ∫<br />
b<br />
a<br />
f(x)dx<br />
Begründung für diese Regeln: Das Integral ist als Grenzwert definiert worden. Für Grenzwerte<br />
gelten bestimmte Re<strong>ch</strong>enregeln, auf die hier verwiesen wird.<br />
Beispiel:<br />
2π<br />
π<br />
2π<br />
∫sin x dx = 0<br />
∫sin x dx + π<br />
∫sin x dx = 0<br />
0<br />
1<br />
0<br />
π<br />
2π<br />
-1<br />
Wie aus der Zei<strong>ch</strong>nung ersi<strong>ch</strong>tli<strong>ch</strong> ist, haben die beiden Teilflä<strong>ch</strong>en dieselbe Grösse. Die beiden<br />
Teilintegrale haben aber unters<strong>ch</strong>iedli<strong>ch</strong>es Vorzei<strong>ch</strong>en, sodass das Gesamtintegral Null wird.<br />
A<strong>ch</strong>tung: Bei Flä<strong>ch</strong>enbere<strong>ch</strong>nungen darf ni<strong>ch</strong>t über Nullstellen wegintegriert werden.<br />
© 1990- 2003 by Hermann Knoll ver. 4.0 / 06.10.2003
<strong>Integralre<strong>ch</strong>nung</strong><br />
Mathematik<br />
102<br />
Das unbestimmte Integral<br />
a<br />
b<br />
∫f(x)dx ist das bestimmte Integral einer Funktion f(x) in den Grenzen a bis b. Der Wert dieses Integrals<br />
hängt von der Grösse der Grenzen a und b ab. Wir werden jetzt eine Grenze variieren lassen.<br />
Der Wert des Integrals hängt dann von dieser variablen Grenze ab, er ist eine Funktion dieser<br />
Grenze.<br />
Φ(x) = ∫<br />
a<br />
x<br />
f(t)dt Φ(x) ist ein unbestimmtes Integral der Funktion f.<br />
Ψ(x) = ∫ α<br />
x<br />
f(t)dt Ψ(x) ist ein anderes unbestimmtes Integral der Funktion f.<br />
Wenn die untere Grenze variabel ist, sind die Verhältnisse glei<strong>ch</strong>.<br />
Satz: Zwei unbestimmte Integrale derselben Funktion f unters<strong>ch</strong>eiden si<strong>ch</strong> nur dur<strong>ch</strong> einen konstanten<br />
Summand.<br />
Beweis:<br />
Φ(x) − Ψ(x) = ∫<br />
a<br />
x<br />
f(t)dt - ∫ α<br />
x<br />
f(t)dt = ∫<br />
a<br />
x<br />
f(t)dt + ∫<br />
x<br />
α<br />
f(t)dt) = ∫<br />
a<br />
α<br />
f(t)dt = C = konstant<br />
Es sei F(x) = Φ(x) + C. Die Funktion F(x) ist ein unbestimmtes Integral. Lässt man C dur<strong>ch</strong> alle<br />
reelle Zahlen laufen, erhält man alle unbestimmten Integrale zur Integrandfunktion f. Wir definieren<br />
allgemein das unbestimmte Integral:<br />
∫f(x)dx = F(x) = Φ(x) + C = ∫<br />
a<br />
x<br />
f(t)dt + C<br />
Kernsatz der Differential und <strong>Integralre<strong>ch</strong>nung</strong><br />
Es sei f(x) eine stetige Funktion und F(x) die Integralfunktion F(x) = ∫f(x)dx.<br />
Satz: Die 1. Ableitung der Integralfunktion F(x) ist glei<strong>ch</strong> ihrer Integrandfunktion f(x).<br />
oder:<br />
Das Integrieren ist die Umkehrung des Differenzierens.<br />
ΔF(x) F(x + Δx) - F(x)<br />
Δx<br />
=<br />
Δx<br />
= 1 x + Δx<br />
x<br />
Δx<br />
⎣ ⎢⎢⎡ ∫f(t)dt - ∫<br />
⎦ ⎥⎥⎤<br />
a<br />
f(t)dt = 1 Δx<br />
⎣ ⎢⎢⎡<br />
a<br />
x + Δx<br />
a<br />
∫f(t)dt + ∫<br />
a<br />
⎦ ⎥⎥⎤<br />
x<br />
f(t)dt = 1 Δx<br />
x + Δx<br />
x<br />
∫<br />
f(t)dt<br />
f(x )<br />
o<br />
Für Δx > 0 und f(x) ≥ 0 gilt:<br />
f(x u )Δx ≤<br />
x + Δx<br />
x<br />
∫<br />
f(t)dt ≤ f(x o )Δx | :Δx<br />
x<br />
f(x<br />
u)<br />
x o<br />
x u<br />
x + Δx<br />
x u sei jene Stelle, an der der Funktionswert am<br />
kleinsten im Intervall (x, x + Δx) ist, x o ist die<br />
Stelle mit dem grössten Funktionswert.<br />
Δx → 0<br />
1<br />
Die 1. Ableitung der Funktion F(x) ist dann F'(x) = lim<br />
Δx→0<br />
Δx<br />
f(x u ) ≤ 1 Δx<br />
f(x)<br />
x + Δx<br />
x<br />
∫f(t)dt ≤ f(x o )<br />
f(x)<br />
f(x)<br />
Für Δx < 0 und f(x) ≤ 0 kann die Überlegung,<br />
die zum Grenzwert führt, analog gema<strong>ch</strong>t<br />
werden.<br />
x + Δx<br />
x<br />
∫<br />
f(t)dt = f(x). Damit ist der Satz bewiesen.<br />
© 1990- 2003 by Hermann Knoll ver. 4.0 / 06.10.2003
<strong>Integralre<strong>ch</strong>nung</strong><br />
Mathematik<br />
103<br />
Stammfunktion<br />
Die Integralfunktion F(x) = ∫f(x)dx heisst Stammfunktion der Funktion f(x), weil gilt: F'(x) = f(x).<br />
Zusammenhang zwis<strong>ch</strong>en bestimmten und unbestimmten Integral<br />
F(x) = Φ(x) + C = ∫<br />
a<br />
x<br />
f(t)dt + C<br />
F(a) = Φ(a) + C = ∫<br />
a<br />
a<br />
f(t)dt + C = C<br />
F(b) = Φ(b) + C = ∫<br />
a<br />
b<br />
f(t)dt + C = ∫<br />
a<br />
b<br />
f(t)dt + F(a)<br />
∫f(x)dx = F(b) - F(a) = [ F(x) ]<br />
b a<br />
a<br />
b<br />
Das bestimmte Integral kann bere<strong>ch</strong>net werden, indem man zuerst die Stammfunktion zur<br />
Integrandfunktion bestimmt und die Differenz aus den Werten der Stammfunktion na<strong>ch</strong> Einsetzen<br />
der oberen und unteren Integrationsgrenzen bildet. Regeln für die planmässige Su<strong>ch</strong>e na<strong>ch</strong> den<br />
Stammfunktionen können aus den Ableitungsregeln gewonnen werden.<br />
Grundintegrale<br />
∫x n dx = xn+1<br />
n+1<br />
+ C für n ≠ -1<br />
∫ dx<br />
x = ln | x | + C<br />
∫e x dx = e x + C<br />
∫a x dx = ax<br />
ln a + C<br />
∫sin x dx = -cos x + C<br />
∫cos x dx = sin x + C<br />
∫ dx<br />
cos 2 x = tan x + C<br />
∫ dx<br />
sin 2 x = -cot x + C<br />
∫ dx<br />
1 - x 2 = arcsin x + C<br />
∫ dx<br />
1 + x 2 = arctan x + C<br />
∫sinh x dx = cosh x + C<br />
∫cosh x dx = sinh x + C<br />
Aus den Ableitungsregeln können weitere Integralformeln entnommen werden.<br />
© 1990- 2003 by Hermann Knoll ver. 4.0 / 06.10.2003