Geometrische Optik
Geometrische Optik
Geometrische Optik
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
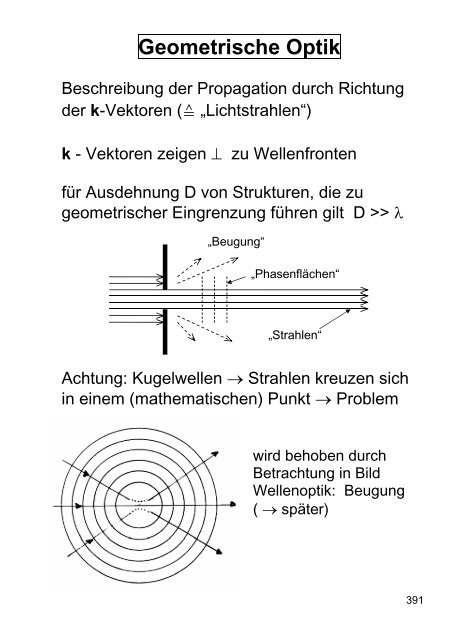
<strong>Geometrische</strong> <strong>Optik</strong><br />
Beschreibung der Propagation durch Richtung<br />
der k-Vektoren (≙ „Lichtstrahlen“)<br />
k - Vektoren zeigen ⊥ zu Wellenfronten<br />
für Ausdehnung D von Strukturen, die zu<br />
geometrischer Eingrenzung führen gilt D >> λ<br />
„Beugung“<br />
„Phasenflächen“<br />
„Strahlen“<br />
Achtung: Kugelwellen → Strahlen kreuzen sich<br />
in einem (mathematischen) Punkt → Problem<br />
wird behoben durch<br />
Betrachtung in Bild<br />
Wellenoptik: Beugung<br />
( → später)<br />
391
dn<br />
0<br />
d r<br />
=<br />
Lichtstrahlen<br />
� Verhalten im freien Raum, optisch homogen,<br />
→ „Strahlen“ = Geraden<br />
� Verhalten an Grenzflächen: Snellius-Gesetz<br />
� Überlagerung von Strahlen: bei linearer <strong>Optik</strong> (I < I*):<br />
Superposition, keine Wechselwirkung zwischen<br />
Bündeln von Strahlen<br />
392
Fermat´sches Prinzip<br />
Weg der Strahlen verläuft so, dass Laufzeit von<br />
A nach B minimal wird<br />
Fermat-Prinzip bei der Reflexion<br />
hier:<br />
Fermat: α1 = α2<br />
Fermat-Prinzip bei der Brechung<br />
α<br />
α1<br />
β<br />
α2<br />
dn 0<br />
dr ≠<br />
n1<br />
n2 > n1<br />
Fermat: n1 sin α1 = n2 sin<br />
393
„Abbildung“<br />
vom Objekt-Punkt gehen Kugelwellen aus<br />
charakterisiert durch Strahlen:<br />
Zusammenführung einer Schar dieser Strahlen<br />
(durch „abbildende“ optische Elemente)<br />
in einem anderen Punkt im Raum: Bildpunkt<br />
Po<br />
<strong>Optik</strong><br />
PB<br />
394
ebener Spiegel ist<br />
das einzige optische<br />
Element mit „idealer“<br />
Abbildung P → P´<br />
“virtuelles“ Bild<br />
alle von P ausgehenden Strahlen scheinen von P´<br />
auszugehen<br />
Abbildung durch<br />
Spiegel<br />
Einfluss des<br />
Sehvorganges<br />
395
Abbildung durch „Lochkamera“<br />
Abbildung hier: Punkt P → Kreisscheibe um P´<br />
Strahlensatz<br />
Φ Kreis (P´):<br />
d' d<br />
=<br />
a b a<br />
( + )<br />
d'<br />
=<br />
( + )<br />
da b<br />
a<br />
durch Abstand und Lochdurchmesser<br />
gegeben<br />
396
optimaler Durchmesser der Blende bei Lochkamera<br />
wenn Lochdurchmesser (zu) groß<br />
→ schlechte Auflösung<br />
Überlapp der Kreisscheiben um P´<br />
wenn Lochdurchmesser (zu) klein<br />
→ schlechte Auflösung<br />
(Beugung an der Öffnung, siehe später)<br />
397
Abbildung durch optische Elemente<br />
Analyse der geometrischen Zusammenhänge der<br />
Strahlengänge und Oberflächen-Topographie<br />
geschickte Auswahl charakteristischer Strahlen<br />
wie z.B. : Dreiecks-Regeln und Strahlensätze<br />
liefert Zusammenhänge zwischen<br />
Eingangsparametern und dem weiterem Verlauf<br />
der Strahlen<br />
„Rechnungen“: mit Buch selber nachvollziehen<br />
wichtig: Reflexion an ebenem Spiegel und an<br />
gekrümmter Spiegelfläche<br />
Brechung an ebener Grenzfläche und an<br />
gekrümmter Grenzfläche (n1 / n2)<br />
daraus aufbauen mit Matrix-Methode:<br />
Strahlengang in komplexeren Systemen<br />
398
Kugelfläche<br />
Hohlspiegel<br />
R<br />
2cosα<br />
FM cos α = ½ R<br />
1<br />
2cosα<br />
OF = R - FM = R - = R ( 1 - )<br />
für kleine Winkel α ( h/R
Charakteristische Strahlen<br />
Konstruktion eines Bildpunktes<br />
für h/R
h h<br />
tanγ=<br />
≈ ≈γ<br />
g g<br />
( −ε)<br />
h<br />
tanβ≈<br />
≈β<br />
b<br />
zur Abbildung durch Hohlspiegel<br />
Krümmungsmittelpunkt<br />
∆SAM = α + γ + 180 o - δ = 180 o → α + γ = δ<br />
δ = α + γ ß = δ + α<br />
δ = - α + ß → 2 δ = γ + ß<br />
1 1 2 1<br />
+ ≈ ≈<br />
g b R f<br />
h<br />
R<br />
Näherung für
Hohlspiegel (achsen-ferne Strahlen)<br />
Kugelfläche<br />
für achsen-ferne Strahlen<br />
f<br />
h<br />
R<br />
gilt Näherung
s 1 = f - x<br />
1 2<br />
2<br />
( ) 2 2<br />
s = f− x + y<br />
( ) ( ) 2 2<br />
s= s + s = f− x + f− x + y<br />
für y 2 = 4 f x (Parabel) →<br />
( ) ( ) 2<br />
s= f− x + f− x = 2f<br />
Parabol-Spiegel<br />
unabhängig von h !<br />
ALLE Achsen-parallelen Strahlen schneiden sich nach<br />
der Reflexion in einem Punkt<br />
(jedoch: schlechte Abbildungseigenschaften bei<br />
Abweichung von Parallelität zu den Achsen)<br />
403
Empfänger<br />
Empfänger<br />
Parabol-Teleskop<br />
Da Objekte sehr weit entfernt, sind die sehr guten<br />
Fokussierungsbedingungen bei korrekter Ausrichtung<br />
der Achse auf Beobachtungsgebiet gegeben.<br />
404
für<br />
dδ 2sin γ dn<br />
λ 1−n sin γ λ<br />
1<br />
2<br />
= ⋅<br />
d 2 2 12 d<br />
dn<br />
≠0→ δ=δ λ<br />
dλ Prismen<br />
( )<br />
δ = δ (α, γ, n(λ) )<br />
aus Brechungsgesetz folgt:<br />
minimale Ablenkung δ für α 1 = α 2 →<br />
symmetrischer Durchgang (AC = BC)<br />
Strahlen im Prisma ⊥ Winkelhalbierende (γ/2)<br />
Konsequenz von Dispersion:<br />
→ Farbzerlegung des Lichtes<br />
da (i.d.R.) n blau > n rot → δ blau > δ rot<br />
vergleiche Beugung (später !) δ blau < δ rot<br />
405
Abbildung<br />
durch gekrümmte<br />
Grenzflächen<br />
(führt auf Abbildungsgleichungen für Linsen)<br />
406
f<br />
Brechung an<br />
sphärisch gekrümmten Grenzflächen<br />
2<br />
Rα<br />
=<br />
α−β<br />
( )<br />
n<br />
2 f2= R<br />
n2 −n1<br />
f 2 ↔ R, n<br />
ß + γ + 180° - α = 180°<br />
h = R sin α = AF sin γ h /R
Matrix-Verfahren<br />
in der geometrischen <strong>Optik</strong><br />
Propagation achsennaher Strahlen mit<br />
geringem Winkel gegen die Achse<br />
Geometrie:<br />
zylindersymmetrisch um die Achse<br />
408
Propagation im freien Raum<br />
α1 = αo<br />
r1 = (x1 - xo ) tan αo + r o ≈ αo (x1 - xo ) + r o<br />
T �<br />
mit Kleinwinkel-Näherung tan αo ≈ αo<br />
(x1 - xo ) = d<br />
r1 = αo d + r o<br />
α1 1 0 αo<br />
=<br />
·<br />
r1 d 1 r o<br />
im Hinblick auf Brechung (n1 α = n2 ß)<br />
wird statt (α) die Größe (nα α) transformiert<br />
n α1 1 0 n αo<br />
=<br />
·<br />
r1 d/n 1 r o<br />
1 0<br />
Propagation = Translations-Matrix<br />
d/n 1<br />
ro<br />
xo<br />
d<br />
x1<br />
r1<br />
Strahl<br />
α<br />
Achse<br />
409
Reflexion am Hohlspiegel (n = 1)<br />
r<br />
R<br />
1<br />
tan (α + α1) = - ≈ (α + α1)<br />
r<br />
1<br />
α2 = - α1 - 2 r2 = r1<br />
R<br />
R �<br />
M<br />
Winkel jeweils zur Achse hin gemessen<br />
α2 = 2 α + α1 = 2 (α + α1) - α1<br />
(„ - “ wg. Richtungsumkehr, + x → - x )<br />
α2 -1 - 2/R α1<br />
Transformation<br />
hier<br />
R = MP<br />
ε
n<br />
n<br />
2<br />
1<br />
α<br />
= β<br />
r<br />
γ = α2 + ß tan<br />
α = γ + α1<br />
1 γ= =γ<br />
R1<br />
⎛n ⎞ ⎛ 1 n ⎞ 1<br />
α 2 =γ−β=γ−⎜ ⎟α=γ−⎜ ⎟(<br />
γ+α1)<br />
⎝n2⎠ ⎝n2⎠ ⎛ r ⎞ 1<br />
n2α 2 = n2γ−n1γ−n1α 1 =−n1α 1+ ( n2 −n1) ⎜ ⎟<br />
⎝R1⎠ Vorzeichen-Konvention: α2 → - α2<br />
r1<br />
n2α2 = n1α1 + (n1 - n2) ( ) r2 = r1<br />
R1<br />
1<br />
n2α2 1 (n1 - n2) ( ) n1α1<br />
=<br />
R1<br />
r2 0 1 r1<br />
B �<br />
Brechung an gekrümmter Grenzfläche<br />
Brechungsgesetz<br />
n2 ß = n1 α<br />
Beträge der Winkel betrachtet<br />
1<br />
1 (n1 - n2) ( )<br />
R<br />
= 1 Brechungsmatrix<br />
0 1<br />
411
n1 α1<br />
r<br />
Transformations-Matrix für allgemeinen Fall<br />
Translation Translation Translation<br />
Brechung Brechung<br />
n1 α1 n2 α2 n2 α2 n3 α3<br />
→ → →<br />
r1 r1 r2 r2<br />
n3 α3<br />
r’<br />
412
Transformation durch Brechungen und Translation<br />
n1α1 n2α2 n2α2 n3α3<br />
B� B� T� → 1 → → 12 → → 2 →<br />
r1 r1 r2 r2<br />
n3α3 n1α1 n1α1<br />
B� T� B� M� = 2 12 1 =<br />
r2 r1 r1<br />
M� 1<br />
1<br />
1 (n2 - n3)( ) 1 0 1 (n1 - n2)( )<br />
=<br />
R2 ·<br />
R1<br />
d<br />
·<br />
0 1 1 0 1<br />
n<br />
für d = 0 → „dünne“ Linse<br />
mit n2 = n und n1 = n3 = 1 →<br />
M<br />
1<br />
f<br />
� ( )<br />
düLi =<br />
1 -<br />
0 1<br />
2<br />
1 1 1<br />
= n−1 ( − )<br />
f R R<br />
1 2<br />
413
Beispiel: dünne Linse<br />
„dünn“: Ausdehnung der Linse spielt keine Rolle<br />
y<br />
„Brechung“ in der Mittelebene der Linse<br />
(a) (b) (c)<br />
Transformation von Achsen-parallelem Strahl<br />
Brechung an die Mittenebene der Linsen:<br />
y → y´ α (= 0) → α´ tan α´ ≈ α´ = - y / f<br />
α´ 1 0 0 α´ 1 -1/f 0<br />
y´ x 1 y y´ 0 1 y<br />
T� M� Translation: Brechung: dünn<br />
(b) → (c) bei (b)<br />
T� M� zusammen: (α´, y) = dünn (0, y)<br />
α´ 1 -1/f 0 - y/f<br />
=<br />
=<br />
y´ x -x/f + 1 y (-x/f + 1) y<br />
y´<br />
für x = f wird y´ = 0 (wie erwartet)<br />
xf<br />
α´<br />
414
⎛ cosϑ<br />
⎞<br />
∆= dsinϑ⎜1−⎟ 2 2<br />
⎝ n −sin ϑ⎠<br />
„dünne“ Linsen<br />
für „dünne Linsen“ angenommen: ∆ → 0<br />
Vernachlässigung des Strahlversatzes<br />
415