- Page 2:
Walter R. Johnson Atomic Structure
- Page 6:
Professor Dr. Walter R. Johnson Uni
- Page 10:
Preface This is a set of lecture no
- Page 14:
Contents 1 Angular Momentum .......
- Page 18:
Contents XI 6 Radiative Transitions
- Page 22:
1 Angular Momentum Understanding th
- Page 26:
1.1 Orbital Angular Momentum - Sphe
- Page 30:
1.1 Orbital Angular Momentum - Sphe
- Page 34:
Θl,m(θ) = (−1)l 2 l l! 1.1 Orbi
- Page 38:
1.2 Spin Angular Momentum 9 The Pau
- Page 42:
The matrix s 2 = s 2 x + s 2 y + s
- Page 46:
1.3 Clebsch-Gordan Coefficients 13
- Page 50:
1.3 Clebsch-Gordan Coefficients 15
- Page 54:
1.3 Clebsch-Gordan Coefficients 17
- Page 58:
1.4 Graphical Representation - Basi
- Page 62:
1.4 Graphical Representation - Basi
- Page 66:
1.5 Spinor and Vector Spherical Har
- Page 70:
aJLM = µν 1.5 Spinor and Vector
- Page 74:
1.5 Spinor and Vector Spherical Har
- Page 78:
2 Central-Field Schrödinger Equati
- Page 82:
2.2 Coulomb Wave Functions 2.2 Coul
- Page 86:
2.2 Coulomb Wave Functions 33 Pnℓ
- Page 90:
and for σ = −(s +1)≤−1, J (
- Page 94:
2.3.1 Adams Method (adams) 2.3 Nume
- Page 98:
2.3 Numerical Solution to the Radia
- Page 102:
2.3 Numerical Solution to the Radia
- Page 106:
2.3 Numerical Solution to the Radia
- Page 110:
2.3 Numerical Solution to the Radia
- Page 114:
2.4 Quadrature Rules (rint) 47 wher
- Page 118:
2.5 Potential Models 49 with ζ = Z
- Page 122:
2.5 Potential Models 51 examining t
- Page 126:
Substituting for ρ(r) from (2.104)
- Page 130:
2.6 Separation of Variables for Dir
- Page 134:
2.7 Radial Dirac Equation for a Cou
- Page 138:
2.7 Radial Dirac Equation for a Cou
- Page 142:
P n (r) and Q n (r)/(Z) 0.4 0.0 -0.
- Page 146:
2.8 Numerical Solution to Dirac Equ
- Page 150:
2.8 Numerical Solution to Dirac Equ
- Page 154:
2.8 Numerical Solution to Dirac Equ
- Page 158:
2.8 Numerical Solution to Dirac Equ
- Page 162:
3 Self-Consistent Fields In this ch
- Page 166:
3.1 Two-Electron Systems 73 The fac
- Page 170:
3.1 Two-Electron Systems 75 indepen
- Page 174:
3.2 HF Equations for Closed-Shell A
- Page 178:
3.2 HF Equations for Closed-Shell A
- Page 182:
3.2 HF Equations for Closed-Shell A
- Page 186:
We may then write Rl(a, b, c, d) =
- Page 190:
3.2 HF Equations for Closed-Shell A
- Page 194:
3.2 HF Equations for Closed-Shell A
- Page 198:
3.3 Numerical Solution to the HF Eq
- Page 202:
3.3 Numerical Solution to the HF Eq
- Page 206:
3.4 Atoms with One Valence Electron
- Page 210:
3.4 Atoms with One Valence Electron
- Page 214:
3.5 Dirac-Fock Equations 97 Table 3
- Page 218:
3.5 Dirac-Fock Equations 99 ϕ †
- Page 222:
3.5 Dirac-Fock Equations 101 ∞
- Page 226:
3.5 Dirac-Fock Equations 103 solvin
- Page 230:
3.5 Dirac-Fock Equations 105 Table
- Page 234:
108 4 Atomic Multiplets 〈k| = 〈
- Page 238:
110 4 Atomic Multiplets 〈ab ··
- Page 242:
112 4 Atomic Multiplets product sta
- Page 246:
114 4 Atomic Multiplets where ∆(j
- Page 250:
116 4 Atomic Multiplets E (1) ab,LS
- Page 254:
118 4 Atomic Multiplets formally de
- Page 258:
120 4 Atomic Multiplets Here E0 =
- Page 262:
122 4 Atomic Multiplets As specific
- Page 266:
124 4 Atomic Multiplets then an ext
- Page 270:
126 4 Atomic Multiplets It follows
- Page 274:
128 4 Atomic Multiplets A useful sp
- Page 278:
130 4 Atomic Multiplets have droppe
- Page 282:
132 4 Atomic Multiplets E( 2S+1 P )
- Page 286:
134 4 Atomic Multiplets Problems 1
- Page 290:
5 Hyperfine Interaction & Isotope S
- Page 294:
5.1 Hyperfine Structure 139 If we l
- Page 298:
where 5.1 Hyperfine Structure 141
- Page 302:
5.2 Atoms with One Valence Electron
- Page 306:
5.2 Atoms with One Valence Electron
- Page 310:
Let us transform to relative coordi
- Page 314:
5.4 Calculations of the SMS 149 whe
- Page 318:
Relativistic Case 5.4 Calculations
- Page 322:
5.5 Field Shift 153 For a uniform c
- Page 326:
5.5 Field Shift 155 fbb = ∞ drPb
- Page 330:
6 Radiative Transitions In this cha
- Page 334:
6.1 Review of Classical Electromagn
- Page 338:
i 6.2 Quantized Electromagnetic Fie
- Page 342:
6.2.3 Time-Dependent Perturbation T
- Page 346:
For the case of photon absorption,
- Page 350:
6.2 Quantized Electromagnetic Field
- Page 354:
6.2 Quantized Electromagnetic Field
- Page 358:
6.2 Quantized Electromagnetic Field
- Page 362:
6.2 Quantized Electromagnetic Field
- Page 366:
6.2 Quantized Electromagnetic Field
- Page 370:
6.2 Quantized Electromagnetic Field
- Page 374:
6.2 Quantized Electromagnetic Field
- Page 378:
6.2 Quantized Electromagnetic Field
- Page 382: 6.2 Quantized Electromagnetic Field
- Page 386: 6.3 Theory of Multipole Transitions
- Page 390: A(r,ω)=4π JLM 6.3 Theory of Mult
- Page 394: 6.3 Theory of Multipole Transitions
- Page 398: 6.3 Theory of Multipole Transitions
- Page 402: 6.3 Theory of Multipole Transitions
- Page 406: 196 7 Introduction to MBPT H0Ψ0 =
- Page 410: 198 7 Introduction to MBPT The firs
- Page 414: 200 7 Introduction to MBPT The indi
- Page 418: 202 7 Introduction to MBPT E (3) =
- Page 422: 204 7 Introduction to MBPT B nk (r)
- Page 426: 206 7 Introduction to MBPT quantum
- Page 430: 208 7 Introduction to MBPT Table 7.
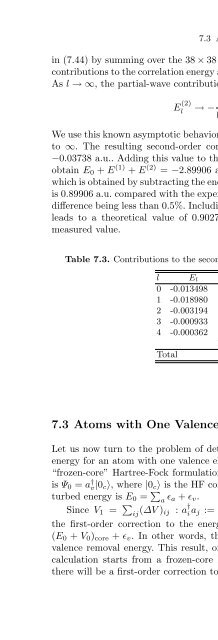
- Page 436: 7.3.2 Angular Momentum Decompositio
- Page 440: 7.3 Atoms with One Valence Electron
- Page 444: 7.3 Atoms with One Valence Electron
- Page 448: 7.4 Relativistic Calculations 217 s
- Page 452: The radial matrix elements ML(ijkl)
- Page 456: 7.4 Relativistic Calculations 221 o
- Page 460: 7.4 Relativistic Calculations 223 2
- Page 464: where ηkl is a symmetry factor def
- Page 468: 7.6 MBPT for Divalent Atoms and Ion
- Page 472: 7.6 MBPT for Divalent Atoms and Ion
- Page 476: 7.7 Second-Order Perturbation Theor
- Page 480: 7.7 Second-Order Perturbation Theor
- Page 484:
(b) 7.2. Prove: (a) (b) 0c mambmmm
- Page 488:
8 MBPT for Matrix Elements In Chapt
- Page 492:
8.1 Second-Order Corrections 239 Ta
- Page 496:
t RPA am = tam + bn t RPA ma = tma
- Page 500:
8.2 Random-Phase Approximation 243
- Page 504:
8.3 Third-Order Matrix Elements 245
- Page 508:
8.4 Matrix Elements of Two-Particle
- Page 512:
Energy (a.u.) 10 1 10 0 10 -1 10 -2
- Page 516:
8.5 CI Calculations for Two-Electro
- Page 520:
8.6 Second-Order Matrix Elements in
- Page 524:
8.6 Second-Order Matrix Elements in
- Page 528:
T (2) deriv (−1)J [JI][JF ] v≤
- Page 532:
8.7 Summary Remarks 259 8.2. Consid
- Page 536:
262 Solutions From the above, it fo
- Page 540:
264 Solutions l = 4 t := Table[(-1)
- Page 544:
266 Solutions This, in turn, can be
- Page 548:
268 Solutions top := top*(a+k-1); b
- Page 552:
270 Solutions P[n_, l_, r_] = Sqrt[
- Page 556:
272 Solutions Energies for Na from
- Page 560:
274 Solutions One finds [H, rk] =[c
- Page 564:
276 Solutions The S = 1 eigenstates
- Page 568:
278 Solutions (3s1/2 3s1/2) → [0]
- Page 572:
280 Solutions Thesumsoverµ’s ass
- Page 576:
282 Solutions 〈F |VI|I〉 = 1 gi
- Page 580:
284 Solutions δν =5× 3 4 × 0.91
- Page 584:
286 Solutions 5.5 Normal Mass Shift
- Page 588:
288 Solutions Extracting the coeffi
- Page 592:
290 Solutions 6.3 The Al ground sta
- Page 596:
292 Solutions 6.4 Heliumlike B: (a)
- Page 600:
294 Solutions (d) The 5d 3/2 state
- Page 604:
296 Solutions (c) He (1s2s) 3 S1- T
- Page 608:
298 Solutions where, χ (1) ma =
- Page 612:
300 Solutions Problems of Chapter 8
- Page 616:
302 Solutions i∆T (2) wv = χam
- Page 620:
304 References [17] A. R. Edmonds.
- Page 624:
Index LS coupled states first-order
- Page 628:
graphical rules 3j symbols, 20 arro
- Page 632:
second quantization, 107 second-ord