Properties of the Triangle of Excentres
Properties of the Triangle of Excentres
Properties of the Triangle of Excentres
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
<strong>Properties</strong> <strong>of</strong> <strong>the</strong> <strong>Triangle</strong> <strong>of</strong> <strong>Excentres</strong><br />
Christopher Bradley<br />
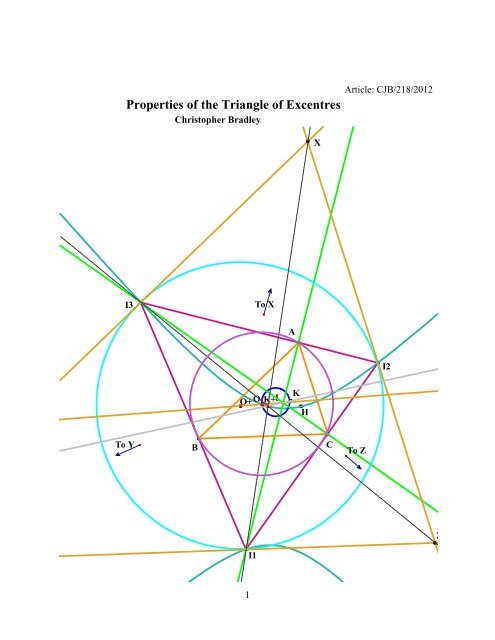
I3<br />
To Y<br />
B<br />
1<br />
I1<br />
To X<br />
O+ O K+ I<br />
A<br />
K<br />
H<br />
X<br />
C<br />
Article: CJB/218/2012<br />
To Z<br />
I2<br />
Z
Abstract: In <strong>the</strong> triangle <strong>of</strong> excentres <strong>the</strong> orthocentre is <strong>the</strong> incentre I <strong>of</strong> ABC, <strong>the</strong> Symmedian<br />
point K+ is <strong>the</strong> Mittenpunkt <strong>of</strong> ABCand <strong>the</strong> nine-point centre is <strong>the</strong> circumcentre O <strong>of</strong> ABC. The<br />
circumcentre O+ lies on <strong>the</strong> line OI and is such that O+O = OI. These properties are proved as<br />
also <strong>the</strong> fact that KI passes through K+.<br />
1. Circle I1I2I3 and its tangents<br />
The co-ordinates <strong>of</strong> <strong>the</strong> excentres are I1(– a, b, c), I2(a, – b, c), I3(a, b, – c). It is easy to check that<br />
<strong>the</strong> equation <strong>of</strong> <strong>the</strong> circle I1I2I3 is<br />
a 2 yz + b 2 zx + c 2 xy +(x + y + z)(bcx + cay + abz) = 0. (1.1)<br />
The tangents to this circle at <strong>the</strong> points I1, I2, I3 have equations<br />
I1: (b + c)x + a(y + z) = 0, (1.2)<br />
I2: (c + a)y + b(z + x) = 0, (1.3)<br />
I3: (a + b)z + c(x + y) = 0. (1.4)<br />
Tangents at I2, I3 meet at X with co-ordinates X(– a(a + b + c), b(a + b – c), c(a – b + c)).<br />
Tangents at I3, I1 meet at Y with co-ordinates Y(a(a + b – c), – b(a + b + c),c(b + c – a)).<br />
Tangents at I1, I2 meet at Z with co-ordinates Z(a(c + a – b), b(b + c – a), – c(a + b + c)).<br />
2. The symmedian point K+<br />
The symmedian point K+ <strong>of</strong> triangle I1I2I3 is <strong>the</strong> point <strong>of</strong> concurrence <strong>of</strong> lines XI1, YI2, ZI3<br />
whose equations are respectively<br />
(c – b)x = a(y – z), (a – c)y = b(z – x), (b – a)z = c(x – y). (2.1)<br />
The co-ordinates <strong>of</strong> K+ are <strong>the</strong>refore (a(b + c – a), b(c + a – b), c(a + b – c)). The co-ordinates<br />
will be recognized as those <strong>of</strong> <strong>the</strong> Mittenpunkt Mi, X9 in Kimberling’s list <strong>of</strong> <strong>Triangle</strong> Centres.<br />
It is a well known fact that in triangle I1I2I3 that II1 is perpendicular to I2I3 etc. Hence <strong>the</strong> incentre<br />
I is <strong>the</strong> orthocentre H+ <strong>of</strong> triangle I1I2I3.<br />
From <strong>the</strong> usual formulae for <strong>the</strong> centre <strong>of</strong> a conic we find <strong>the</strong> co-ordinates <strong>of</strong> O+ to be (x, y, z),<br />
where<br />
x = a(a 3 + a 2 (b + c) – a(b + c) 2 – b 3 + b 2 c + bc 2 – c 3 ) (2.2)<br />
2
with y, z following by cyclic change <strong>of</strong> a, b, c. It may now be checked that this is <strong>the</strong> point on IO<br />
such that O+O = OI and hence <strong>the</strong> nine-point centre <strong>of</strong> triangle I1I2I3 is <strong>the</strong> circumcentre O <strong>of</strong><br />
triangle ABC.<br />
The equation <strong>of</strong> <strong>the</strong> line IK is<br />
bc(c – b)x + ca(a – c)y + ab(b – a)z = 0 (2.3)<br />
and it may be checked that K+ lies on this line.<br />
Finally, after some heavy algebra, it may be checked that K+ lies on <strong>the</strong> conic I1I2I3OH.<br />
Flat 4,<br />
Terrill Court,<br />
12-14, Apsley Road,<br />
BRISTOL BS8 2SP.<br />
3