Improved ant colony optimization algorithms for continuous ... - CoDE

44 Ant Colony Optimization for Mixed Variable Problems
Probability of solving the problem
0.0 0.2 0.4 0.6 0.8 1.0
10 2
Ackley− categorical variables
10 3
Restart
Dim=2 Dim=6
10 4
Non−restart
10 5
Dim=10
Number of function evaluations
10 6
Probability of solving the problem
0.0 0.2 0.4 0.6 0.8 1.0
10 2
Griewank− categorical variables
Restart
Dim=2 Dim=6
10 3
Non−restart
10 4
10 5
Dim=10
Number of function evaluations
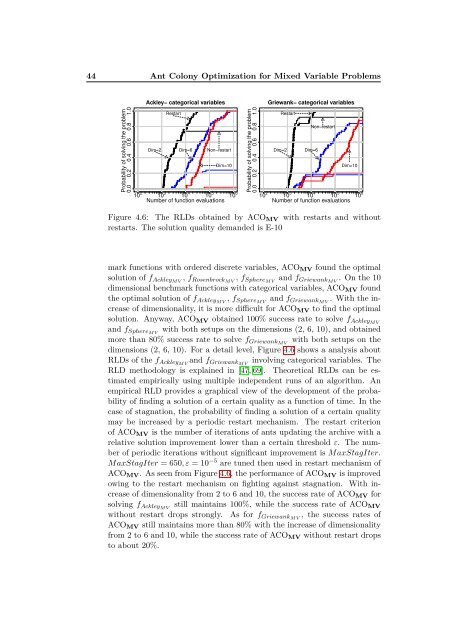
Figure 4.6: The RLDs obtained by ACOMV with restarts and without
restarts. The solution quality demanded is E-10
mark functions with ordered discrete variables, ACOMV found the optimal
solution of fAckleyMV , fRosenbrockMV , fSphereMV and fGriewankMV . On the 10
dimensional benchmark functions with categorical variables, ACOMV found
the optimal solution of fAckleyMV , fSphereMV and fGriewankMV . With the increase
of dimensionality, it is more difficult for ACOMV to find the optimal
solution. Anyway, ACOMV obtained 100% success rate to solve fAckleyMV
and fSphereMV with both setups on the dimensions (2, 6, 10), and obtained
more than 80% success rate to solve fGriewankMV with both setups on the
dimensions (2, 6, 10). For a detail level, Figure 4.6 shows a analysis about
RLDs of the fAckleyMV and fGriewankMV involving categorical variables. The
RLD methodology is explained in [47, 69]. Theoretical RLDs can be estimated
empirically using multiple independent runs of an algorithm. An
empirical RLD provides a graphical view of the development of the probability
of finding a solution of a certain quality as a function of time. In the
case of stagnation, the probability of finding a solution of a certain quality
may be increased by a periodic restart mechanism. The restart criterion
of ACOMV is the number of iterations of ants updating the archive with a
relative solution improvement lower than a certain threshold ε. The number
of periodic iterations without significant improvement is MaxStagIter.
MaxStagIter = 650, ε = 10−5 are tuned then used in restart mechanism of
ACOMV. As seen from Figure 4.6, the performance of ACOMV is improved
owing to the restart mechanism on fighting against stagnation. With increase
of dimensionality from 2 to 6 and 10, the success rate of ACOMV for
solving fAckleyMV still maintains 100%, while the success rate of ACOMV
without restart drops strongly. As for fGriewankMV , the success rates of
ACOMV still maintains more than 80% with the increase of dimensionality
from 2 to 6 and 10, while the success rate of ACOMV without restart drops
to about 20%.
10 6