Efficient linear scaling method for computing the thermal conductivity ...

EFFICIENT LINEAR SCALING METHOD FOR COMPUTING ... PHYSICAL REVIEW B 83, 155416 (2011)
κ (nW/K)
40
35
30
25
20
15
10
5
pristine
L=100 nm
L=500 nm
L=1 μm
L=2 μm
0
0 100 200 300 400 500
Temperature (K)
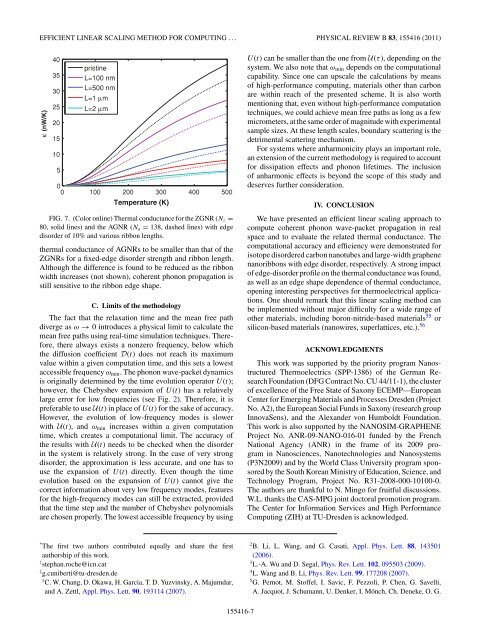
FIG. 7. (Color online) Thermal conductance for the ZGNR (Nz =
80, solid lines) and the AGNR (Na = 138, dashed lines) with edge
disorder of 10% and various ribbon lengths.
thermal conductance of AGNRs to be smaller than that of the
ZGNRs for a fixed-edge disorder strength and ribbon length.
Although the difference is found to be reduced as the ribbon
width increases (not shown), coherent phonon propagation is
still sensitive to the ribbon edge shape.
C. Limits of the methodology
The fact that the relaxation time and the mean free path
diverge as ω → 0 introduces a physical limit to calculate the
mean free paths using real-time simulation techniques. Therefore,
there always exists a nonzero frequency, below which
the diffusion coefficient D(t) does not reach its maximum
value within a given computation time, and this sets a lowest
accessible frequency ωmin. The phonon wave-packet dynamics
is originally determined by the time evolution operator U(t);
however, the Chebyshev expansion of U(t) has a relatively
large error for low frequencies (see Fig. 2). Therefore, it is
preferable to use U(t) in place of U(t) for the sake of accuracy.
However, the evolution of low-frequency modes is slower
with U(t), and ωmin increases within a given computation
time, which creates a computational limit. The accuracy of
the results with U(t) needs to be checked when the disorder
in the system is relatively strong. In the case of very strong
disorder, the approximation is less accurate, and one has to
use the expansion of U(t) directly. Even though the time
evolution based on the expansion of U(t) cannot give the
correct information about very low frequency modes, features
for the high-frequency modes can still be extracted, provided
that the time step and the number of Chebyshev polynomials
are chosen properly. The lowest accessible frequency by using
* The first two authors contributed equally and share the first
authorship of this work.
† stephan.roche@icn.cat
‡ g.cuniberti@tu-dresden.de
1 C. W. Chang, D. Okawa, H. Garcia, T. D. Yuzvinsky, A. Majumdar,
and A. Zettl, Appl. Phys. Lett. 90, 193114 (2007).
155416-7
U(t) can be smaller than the one from U(τ), depending on the
system. We also note that ωmin depends on the computational
capability. Since one can upscale the calculations by means
of high-performance computing, materials other than carbon
are within reach of the presented scheme. It is also worth
mentioning that, even without high-performance computation
techniques, we could achieve mean free paths as long as a few
micrometers, at the same order of magnitude with experimental
sample sizes. At these length scales, boundary scattering is the
detrimental scattering mechanism.
For systems where anharmonicity plays an important role,
an extension of the current methodology is required to account
for dissipation effects and phonon lifetimes. The inclusion
of anharmonic effects is beyond the scope of this study and
deserves further consideration.
IV. CONCLUSION
We have presented an efficient linear scaling approach to
compute coherent phonon wave-packet propagation in real
space and to evaluate the related thermal conductance. The
computational accuracy and efficiency were demonstrated for
isotope disordered carbon nanotubes and large-width graphene
nanoribbons with edge disorder, respectively. A strong impact
of edge-disorder profile on the thermal conductance was found,
as well as an edge shape dependence of thermal conductance,
opening interesting perspectives for thermoelectrical applications.
One should remark that this linear scaling method can
be implemented without major difficulty for a wide range of
other materials, including boron-nitride-based materials 55 or
silicon-based materials (nanowires, superlattices, etc.). 56
ACKNOWLEDGMENTS
This work was supported by the priority program Nanostructured
Thermoelectrics (SPP-1386) of the German Research
Foundation (DFG Contract No. CU 44/11-1), the cluster
of excellence of the Free State of Saxony ECEMP—European
Center for Emerging Materials and Processes Dresden (Project
No. A2), the European Social Funds in Saxony (research group
InnovaSens), and the Alexander von Humboldt Foundation.
This work is also supported by the NANOSIM-GRAPHENE
Project No. ANR-09-NANO-016-01 funded by the French
National Agency (ANR) in the frame of its 2009 program
in Nanosciences, Nanotechnologies and Nanosystems
(P3N2009) and by the World Class University program sponsored
by the South Korean Ministry of Education, Science, and
Technology Program, Project No. R31-2008-000-10100-0.
The authors are thankful to N. Mingo for fruitful discussions.
W.L. thanks the CAS-MPG joint doctoral promotion program.
The Center for Information Services and High Performance
Computing (ZIH) at TU-Dresden is acknowledged.
2B. Li, L. Wang, and G. Casati, Appl. Phys. Lett. 88, 143501
(2006).
3L.-A. Wu and D. Segal, Phys. Rev. Lett. 102, 095503 (2009).
4L. Wang and B. Li, Phys.Rev.Lett.99, 177208 (2007).
5G. Pernot, M. Stoffel, I. Savic, F. Pezzoli, P. Chen, G. Savelli,
A. Jacquot, J. Schumann, U. Denker, I. Mönch, Ch. Deneke, O. G.