Breaking the Stick

G 1 5
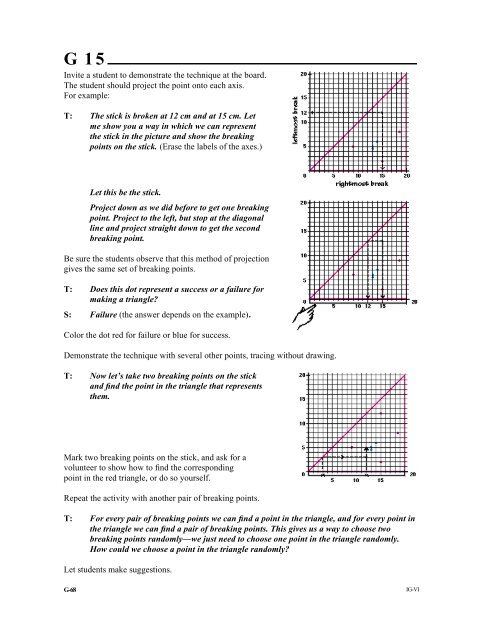
Invite a student to demonstrate the technique at the board.
The student should project the point onto each axis.
For example:
T: The stick is broken at 12 cm and at 15 cm. Let
me show you a way in which we can represent
the stick in the picture and show the breaking
points on the stick. (Erase the labels of the axes.)
Let this be the stick.
Project down as we did before to get one breaking
point. Project to the left, but stop at the diagonal
line and project straight down to get the second
breaking point.
Be sure the students observe that this method of projection
gives the same set of breaking points.
T: Does this dot represent a success or a failure for
making a triangle?
S: Failure (the answer depends on the example).
Color the dot red for failure or blue for success.
Demonstrate the technique with several other points, tracing without drawing.
T: Now let’s take two breaking points on the stick
and find the point in the triangle that represents
them.
Mark two breaking points on the stick, and ask for a
volunteer to show how to find the corresponding
point in the red triangle, or do so yourself.
Repeat the activity with another pair of breaking points.
T: For every pair of breaking points we can find a point in the triangle, and for every point in
the triangle we can find a pair of breaking points. This gives us a way to choose two
breaking points randomly—we just need to choose one point in the triangle randomly.
How could we choose a point in the triangle randomly?
Let students make suggestions.
G-68
IG-VI