Breaking the Stick

G 1 3
Once the class is secure in the triangle construction technique and there are two triangles (short-short-long
and long-long-short) on the board, distribute copies of Worksheet G13(a) which shows five pairs of
line segments. Direct students to construct as many triangles as possible with each pair of segments.
Each side of a triangle must be the same length as one member of the pair, and each line segment of
the related pair must be used at least once. The pairs are denoted A, B, C, D, and E. Instruct students
to mark each triangle with the same letter as the pair of segments used to construct it. As students fill
up the space on the worksheet, provide them with unlined paper.
Encourage accurate and careful constructions. Allow time for experimentation and for the conviction
to grow that in no case are more than two triangles possible. Encourage students to try to formulate
a rule to predict the possibility of one or two triangles, and then to draw pairs of segments to test the
rule. Now students may use the metric rulers for measuring in order to further test a rule based on
relative lengths of the line segments.
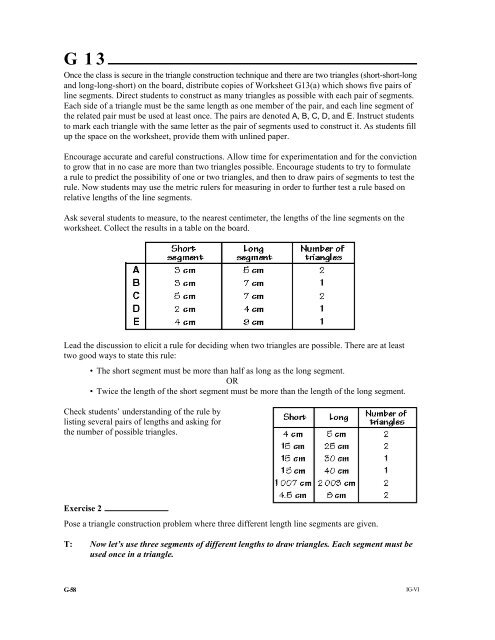
Ask several students to measure, to the nearest centimeter, the lengths of the line segments on the
worksheet. Collect the results in a table on the board.
Lead the discussion to elicit a rule for deciding when two triangles are possible. There are at least
two good ways to state this rule:
• The short segment must be more than half as long as the long segment.
OR
• Twice the length of the short segment must be more than the length of the long segment.
Check students’ understanding of the rule by
listing several pairs of lengths and asking for
the number of possible triangles.
Exercise 2
Pose a triangle construction problem where three different length line segments are given.
T: Now let’s use three segments of different lengths to draw triangles. Each segment must be
used once in a triangle.
G-58 IG-VI