Molecular modelling of entangled polymer fluids under flow The ...

54 CHAPTER 3. THE POM-POM MODEL IN EXPONENTIAL SHEAR.
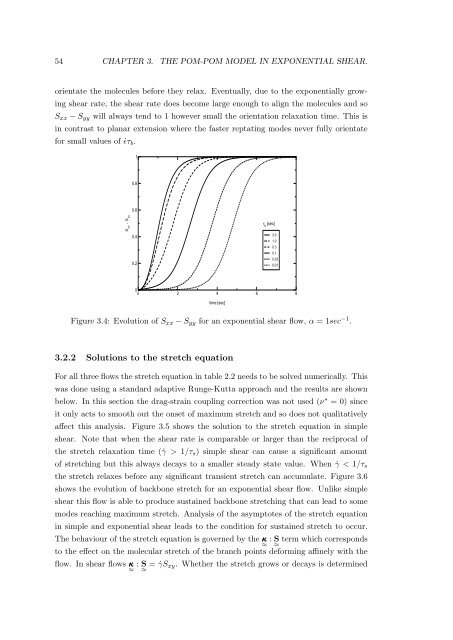
orientate the molecules before they relax. Eventually, due to the exponentially growing
shear rate, the shear rate does become large enough to align the molecules and so
S xx − S yy will always tend to 1 however small the orientation relaxation time. This is
in contrast to planar extension where the faster reptating modes never fully orientate
for small values of ˙ɛτ b .
1
0.8
0.6
S xx - S yy
0.4
0.2
τ b [sec]
3.0
1.0
0.3
0.1
0.03
0.01
0
0 2 4 6 8
time [sec]
Figure 3.4: Evolution of S xx − S yy for an exponential shear flow, α = 1sec −1 .
3.2.2 Solutions to the stretch equation
For all three flows the stretch equation in table 2.2 needs to be solved numerically. This
was done using a standard adaptive Runge-Kutta approach and the results are shown
below. In this section the drag-strain coupling correction was not used (ν ∗ = 0) since
it only acts to smooth out the onset of maximum stretch and so does not qualitatively
affect this analysis. Figure 3.5 shows the solution to the stretch equation in simple
shear. Note that when the shear rate is comparable or larger than the reciprocal of
the stretch relaxation time ( ˙γ > 1/τ s ) simple shear can cause a significant amount
of stretching but this always decays to a smaller steady state value. When ˙γ < 1/τ s
the stretch relaxes before any significant transient stretch can accumulate. Figure 3.6
shows the evolution of backbone stretch for an exponential shear flow. Unlike simple
shear this flow is able to produce sustained backbone stretching that can lead to some
modes reaching maximum stretch. Analysis of the asymptotes of the stretch equation
in simple and exponential shear leads to the condition for sustained stretch to occur.
The behaviour of the stretch equation is governed by the κ
≈
: S
≈
term which corresponds
to the effect on the molecular stretch of the branch points deforming affinely with the
flow. In shear flows κ
≈
: S
≈
= ˙γS xy . Whether the stretch grows or decays is determined