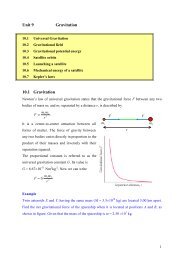
here - Department of Physics, HKU

CHAPTER 3. LORENTZ TRANSFORMATIONS 17
Third, the origin of the stationary system must have x = 0 and x ′ = −vt ′ .
By Eq. (3.3) and Eq. (3.4), for all t,
To summarize up to now, we have
{
x
′
= −vft
t ′ = kt
−vft = −vkt
k = f . (3.6)
x ′ = f(x − vt) (3.7)
t ′ = hx + ft . (3.8)
Fourth, let consider a photon with trajectory x = ct. Since it passes
through the origin of the stationary coordinate system, it also passes through
the origin of the moving coordinate system, x ′ = t ′ = 0. By the second basic
premise of special relativity, it must also have velocity c. Hence, x ′ = ct ′ ,
and
f(x − vt) = x ′
= ct ′ = c(hx + ft)
f(ct − vt) = c(hct + ft)
fc − fv = c 2 h + cf
h = −fv/c 2 . (3.9)
Finally, consider the event that the photon strikes the lower mirror of the
light
√
clock in Section 2.4. It has the coordinates (x, t) = (vt, t) and (x ′ , t ′ ) =
(0, t 1 − v 2 /c 2 ). (Note that we used different notation in Section 2.4.) We
have
t ′ = f(t − vx/c 2 )
√
t 1 − v 2 /c 2 = f(1 − v 2 /c 2 ) t
1
f = √1 − v 2 /c . (3.10)
2
To summarize, we have
x ′ =
x − vt
√1 − v 2 /c 2 (3.11)
y ′ = y (3.12)
z ′ = z (3.13)
t ′ = t − vx/c2 √1 − v 2 /c 2 . (3.14)